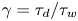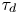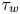1. Introduction
The scrape-off layer (SOL) region of magnetically confined plasmas, as used in experiments on fusion energy, is the interface between the hot fusion plasma and material walls. It functions to direct hot plasma that is exhausted from the closed flux surface volume onto remote targets. In order to develop predictive modelling capability for the expected particle and heat fluxes on plasma facing components of the machine vessel, it is important to develop appropriate methods to characterize the plasma transport processes in the SOL.
In the outboard SOL, blob-like plasma filaments transport plasma and heat from the confined plasma column radially outward toward the main chamber wall. These filaments are elongated along the magnetic field lines and are spatially localized in the radial–poloidal plane. They typically present order-unity relative fluctuations in the plasma pressure. As they constitute the dominant mode of cross-field transport in the SOL, one needs to understand their collective effect on the time-averaged plasma profiles and on the fluctuation statistics of the SOL plasma in order to develop predictive modelling capabilities for the particle and heat fluxes impinging on the plasma-facing components.
Measuring the SOL plasma pressure at a fixed point in space, the footprint of a traversing plasma filament registers as a single pulse. Neglecting the interaction between filaments, a series of traversing blobs results in a time series that is given by a superposition of pulses. Analysis of single-point time-series data, measured in several tokamaks, reveals that they feature several universal statistical properties. First, histograms of single-point time-series data are well described by a gamma distribution (Graves et al. Reference Graves, Horacek, Pitts and Hopcraft2005; Horacek et al. Reference Horacek, Pitts and Graves2005; Garcia et al. Reference Garcia, Cziegler, Kube, LaBombard and Terry2013a,Reference Garcia, Fritzner, Kube, Cziegler, LaBombard and Terryb; Garcia, Horacek & Pitts Reference Garcia, Horacek and Pitts2015; Kube et al. Reference Kube, Theodorsen, Garcia, LaBombard and Terry2016; Theodorsen et al. Reference Theodorsen, Garcia, Horacek, Kube and Pitts2016; Garcia et al. Reference Garcia, Kube, Theodorsen, Bak, Hong, Kim and Pitts2017; Garcia & Theodorsen Reference Garcia and Theodorsen2017; Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018a; Theodorsen et al. Reference Theodorsen, Garcia, Kube, LaBombard and Terry2018; Kuang et al. Reference Kuang, LaBombard, Brunner, Garcia, Kube and Theodorsen2019). Second, conditionally averaged pulse shapes are well described by a two-sided exponential function (Rudakov et al. Reference Rudakov, Boedo, Moyer, Krasheninnikov, Leonard, Mahdavi, McKee, Porter, Stangeby and Watkins2002; Boedo et al. Reference Boedo, Rudakov, Moyer, McKee, Colchin, Schaffer, Stangeby, West, Allen and Evans2003; Kirnev et al. Reference Kirnev, Budaev, Grashin, Gerasimov and Khimchenko2004; Garcia et al. Reference Garcia, Horacek, Pitts, Nielsen, Fundamenski, Naulin and Rasmussen2007; D'Ippolito, Myra & Zweben Reference D'Ippolito, Myra and Zweben2011; Banerjee et al. Reference Banerjee, Zushi, Nishino, Hanada, Sharma, Honma, Tashima, Inoue, Nakamura and Idei2012; Garcia et al. Reference Garcia, Cziegler, Kube, LaBombard and Terry2013a,Reference Garcia, Fritzner, Kube, Cziegler, LaBombard and Terryb; Boedo et al. Reference Boedo, Myra, Zweben, Maingi, Maqueda, Soukhanovskii, Ahn, Canik, Crocker and D'Ippolito2014; Carralero et al. Reference Carralero, Birkenmeier, Müller, Manz, deMarne, Müller, Reimold, Stroth, Wischmeier and Wolfrum2014; Kube et al. Reference Kube, Theodorsen, Garcia, LaBombard and Terry2016; Theodorsen et al. Reference Theodorsen, Garcia, Horacek, Kube and Pitts2016; Garcia et al. Reference Garcia, Kube, Theodorsen, Bak, Hong, Kim and Pitts2017; Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018a). Third, waiting times between consecutive pulses are well described by an exponential distribution. (Adámek et al. Reference Adámek, Stöckel, Hron, Ryszawy, Tichý, Schrittwieser, Ionită, Balan, Martines and Oost2004; Garcia et al. Reference Garcia, Cziegler, Kube, LaBombard and Terry2013a,Reference Garcia, Fritzner, Kube, Cziegler, LaBombard and Terryb, Reference Garcia, Horacek and Pitts2015; Kube et al. Reference Kube, Theodorsen, Garcia, LaBombard and Terry2016; Garcia et al. Reference Garcia, Kube, Theodorsen, Bak, Hong, Kim and Pitts2017; Walkden et al. Reference Walkden, Wynn, Militello, Lipschultz, Matthews, Guillemaut, Harrison, Moulton and Contributors2017; Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018a; Theodorsen et al. Reference Theodorsen, Garcia, Kube, LaBombard and Terry2018). Fourth, frequency power spectral densities (PSDs) of single-point time-series data have a Lorentzian shape. They are flat for low frequencies and decay as a power law for high frequencies. (Garcia et al. Reference Garcia, Horacek and Pitts2015, Reference Garcia, Kube, Theodorsen and Pécseli2016, Reference Garcia, Kube, Theodorsen, Bak, Hong, Kim and Pitts2017; Theodorsen et al. Reference Theodorsen, Garcia, Horacek, Kube and Pitts2016, Reference Theodorsen, Garcia, Kube, LaBombard and Terry2017a, Reference Theodorsen, Garcia, Kube, LaBombard and Terry2018; Garcia & Theodorsen Reference Garcia and Theodorsen2017; Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018a) These statistical properties are robust against changes in plasma parameters and confinement modes.
These universal statistical properties provide a motivation to model the single-point time-series data as a superposition of uncorrelated pulses, arriving according to a Poisson process, using a stochastic model framework. (Garcia Reference Garcia2012; Garcia et al. Reference Garcia, Kube, Theodorsen and Pécseli2016; Militello & Omotani Reference Militello and Omotani2016; Theodorsen & Garcia Reference Theodorsen and Garcia2016; Theodorsen et al. Reference Theodorsen, Garcia, Kube, LaBombard and Terry2017a). In this framework, each pulse corresponds to the footprint of a single plasma filament. Using a two-sided exponential pulse shape, the stochastic model predicts the fluctuations to be gamma distributed. The analytical expression for the frequency PSD of this process has a Lorentzian shape (Garcia & Theodorsen Reference Garcia and Theodorsen2017; Theodorsen, Garcia & Rypdal Reference Theodorsen, Garcia and Rypdal2017b). The framework furthermore links the average pulse duration time ![]() ${\tau _{d}}$ and the average waiting time between consecutive pulses
${\tau _{d}}$ and the average waiting time between consecutive pulses ![]() ${\langle {\tau _{w}} \rangle }$ to the so-called intermittency parameter
${\langle {\tau _{w}} \rangle }$ to the so-called intermittency parameter ![]() $\gamma = {\tau _{d}} / {\langle {\tau _{w}} \rangle }$. This intermittency parameter gives the shape parameter of the gamma distribution that describes the histogram of data time series and also determines the lowest-order statistical moments of the data time series (Garcia Reference Garcia2012). Recently, it has been shown that using either
$\gamma = {\tau _{d}} / {\langle {\tau _{w}} \rangle }$. This intermittency parameter gives the shape parameter of the gamma distribution that describes the histogram of data time series and also determines the lowest-order statistical moments of the data time series (Garcia Reference Garcia2012). Recently, it has been shown that using either ![]() $\gamma$, or
$\gamma$, or ![]() ${\tau _{d}}$ together with
${\tau _{d}}$ together with ![]() ${\langle {\tau _{w}} \rangle }$, each obtained by a different time series analysis method, allow for a consistent parameterization of single-point time-series data (Theodorsen et al. Reference Theodorsen, Garcia, Kube, LaBombard and Terry2018). In order to corroborate the ability of the stochastic model framework to parameterize correctly the relevant dynamics of single-point time-series data measured in SOL plasmas, and in order to establish the validity of using different diagnostics to provide the relevant fluctuation statistics, it is important to compare parameter estimates obtained using a given method and applied to data sampled by different diagnostics measuring the same plasma discharge.
${\langle {\tau _{w}} \rangle }$, each obtained by a different time series analysis method, allow for a consistent parameterization of single-point time-series data (Theodorsen et al. Reference Theodorsen, Garcia, Kube, LaBombard and Terry2018). In order to corroborate the ability of the stochastic model framework to parameterize correctly the relevant dynamics of single-point time-series data measured in SOL plasmas, and in order to establish the validity of using different diagnostics to provide the relevant fluctuation statistics, it is important to compare parameter estimates obtained using a given method and applied to data sampled by different diagnostics measuring the same plasma discharge.
Langmuir probes and gas-puff imaging (GPI) diagnostics are routinely used to diagnose SOL plasmas. Both diagnostics typically sample the plasma with a few megahertz sampling rate and are therefore suitable to study the relevant transport dynamics. Langmuir probes measure the electric current and voltage on an electrode immersed into the plasma. Plasma parameters, such as the electron density and the plasma potential, are commonly calculated assuming a constant electron temperature, whereas in reality the electron temperature also features intermittent large-amplitude fluctuations, similar to the electron density (LaBombard & Lyons Reference LaBombard and Lyons2007; Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018b; Kuang et al. Reference Kuang, LaBombard, Brunner, Garcia, Kube and Theodorsen2019). The rapid biasing that was recently on a scanning probe on Alcator C-Mod (LaBombard & Lyons Reference LaBombard and Lyons2007; LaBombard et al. Reference LaBombard, Golfinopoulos, Terry, Brunner, Davis, Greenwald and Hughes2014), the so-called ‘mirror’ Langmuir probe (MLP), allows measurements of the electron density, electron temperature and the plasma potential on a sub-microsecond time scale. Moreover, GPI diagnostics provide two-dimensional images of emission fluctuations with high time resolution. GPI typically consists of two essential parts. A gas nozzle puffs a contrast gas into the boundary plasma. The puffed gas atoms are excited by local plasma electrons and emit characteristic line radiation modulated by fluctuations in the local electron density and temperature. This emission is sampled by an optical receiver, such as a fast-framing camera or arrays of avalanche photo diodes (APDs) (Terry et al. Reference Terry, Maqueda, Pitcher, Zweben, LaBombard, Marmar, Pigarov and Wurden2001; Cziegler et al. Reference Cziegler, Terry, Hughes and LaBombard2010; Fuchert et al. Reference Fuchert, Birkenmeier, Carralero, Lunt, Manz, Müller, Nold, Ramisch, Rohde and Stroth2014; Zweben et al. Reference Zweben, Terry, Stotler and Maqueda2017). These receivers are commonly arranged in a two-dimensional field of view and encode the plasma fluctuations in a time series of fluctuating emission data. A single channel of the receiver optics is approximated as data from a single spatial point and can be compared with electric probe measurements.
Several comparisons between measurements from GPI and Langmuir probes are found in the literature. Frequency spectra of the SOL plasma in ASDEX (Endler et al. Reference Endler, Niedermeyer, Giannone, Kolzhauer, Rudyj, Theimer and Tsois1995) and Alcator C-Mod (Zweben et al. Reference Zweben, Stotler, Terry, LaBombard, Greenwald, Muterspaugh, Pitcher, Hallatschek, Maqueda and Rogers2002; Terry et al. Reference Terry, Zweben, Hallatschek, LaBombard, Maqueda, Bai, Boswell, Greenwald, Kopon and Nevins2003) calculated from GPI and Langmuir probe measurements are found to agree qualitatively. In other experiments at Alcator C-Mod, it was shown that the fluctuations of the plasma within the same flux tube, measured at different poloidal positions by GPI and a Langmuir probe, show a cross-correlation coefficient of more than ![]() $60\,\%$ (Grulke et al. Reference Grulke, Terry, Cziegler, LaBombard and Garcia2014). A comprehensive overview of GPI diagnostics and comparison with Langmuir probe measurements is given in Zweben et al. (Reference Zweben, Terry, Stotler and Maqueda2017).
$60\,\%$ (Grulke et al. Reference Grulke, Terry, Cziegler, LaBombard and Garcia2014). A comprehensive overview of GPI diagnostics and comparison with Langmuir probe measurements is given in Zweben et al. (Reference Zweben, Terry, Stotler and Maqueda2017).
2. Methods
In this contribution we analyse measurements from the GPI and the MLP diagnostics that were made in three ohmically heated plasma discharges in Alcator C-Mod, confined in a lower single-null diverted magnetic field geometry. The GPI was puffing He and imaging the ![]() $\mathrm {HeI}\, 587\ \mathrm {nm}$ line in these discharges. In addition, we also construct a synthetic signal for the
$\mathrm {HeI}\, 587\ \mathrm {nm}$ line in these discharges. In addition, we also construct a synthetic signal for the ![]() $587\ \mathrm {nm}$ emission line using the
$587\ \mathrm {nm}$ emission line using the ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ time-series data reported by the MLP. All plasma discharges had an on-axis magnetic field strength of
${T_{e}}$ time-series data reported by the MLP. All plasma discharges had an on-axis magnetic field strength of ![]() $B_{T} = 5.4\ {T}$ and a plasma current of
$B_{T} = 5.4\ {T}$ and a plasma current of ![]() $I_{p} = 0.55\ \mathrm {MA}$. The MLPs were connected to the four electrodes of a Mach probe head, installed on the horizontal scanning probe (Brunner et al. Reference Brunner, Kuang, LaBombard and Burke2017). In the analysed discharges, the scanning probe either performs three scans through the SOL per discharge or dwells approximately at the limiter radius for the entire discharge in order to obtain exceptionally long fluctuation time series data. Table 1 lists the line-averaged core plasma density normalized by the Greenwald density (Greenwald Reference Greenwald2002) and the configuration of the horizontal scanning probe for the three analysed discharges. It also lists the average electron density and temperature approximately 8 mm from the last closed flux surface(LCFS), as measured by the MLP and mapped to the outboard mid-plane. These values are representative for the SOL plasma. There is no such data available for discharge 3 because the MLP is dwelled in this case. As discharges 2 and 3 feature almost identical plasma parameters,
$I_{p} = 0.55\ \mathrm {MA}$. The MLPs were connected to the four electrodes of a Mach probe head, installed on the horizontal scanning probe (Brunner et al. Reference Brunner, Kuang, LaBombard and Burke2017). In the analysed discharges, the scanning probe either performs three scans through the SOL per discharge or dwells approximately at the limiter radius for the entire discharge in order to obtain exceptionally long fluctuation time series data. Table 1 lists the line-averaged core plasma density normalized by the Greenwald density (Greenwald Reference Greenwald2002) and the configuration of the horizontal scanning probe for the three analysed discharges. It also lists the average electron density and temperature approximately 8 mm from the last closed flux surface(LCFS), as measured by the MLP and mapped to the outboard mid-plane. These values are representative for the SOL plasma. There is no such data available for discharge 3 because the MLP is dwelled in this case. As discharges 2 and 3 feature almost identical plasma parameters, ![]() ${\langle {n_{e}} \rangle }$ and
${\langle {n_{e}} \rangle }$ and ![]() ${\langle {T_{e}} \rangle }$ are likely to be similar in these two discharges.
${\langle {T_{e}} \rangle }$ are likely to be similar in these two discharges.
Table 1. List of the line-averaged core plasma density normalized to the Greenwald density, the average electron density and temperature at ![]() $\rho \approx 8\ \mathrm {mm}$, and the operational mode of the horizontal scanning probe.
$\rho \approx 8\ \mathrm {mm}$, and the operational mode of the horizontal scanning probe.

Figure 1 shows a cut-out of the cross-section of the Alcator C-Mod tokamak. Overlaid are the views of the GPI diodes, the trajectory of the scanning probe head, as well as the position of the LCFS, obtained from magnetic equilibrium reconstruction (Lao et al. Reference Lao, John, Stambaugh, Kellman and Pfeiffer1985). The position of the scanning probe in the dwelling position as well as the position of the GPI views used in this study are highlighted.

Figure 1. A poloidal cross-section of Alcator C-Mod's outboard mid-plane region showing the LCFS (purple line), magnetic flux surfaces in the SOL (green lines), the views of the APDs (cyan dots, red dots show the diode views used in this study), the trajectory of the MLP when scanning (black arrow) and the position where the MLP dwells during discharge 3 (green dot).
2.1. Calculation of synthetic GPI data
GPI diagnostics are routinely used to measure and visualize fluctuations of the boundary plasma. As realized on Alcator C-Mod, GPI utilizes a vertical stack of four ‘barrels’, located approximately ![]() $1.5\ \mathrm {cm}$ beyond the outermost column of views, see figure 1, to puff a contrast gas into the boundary plasma. The line emission arising from the interaction between the gas atoms and the plasma are captured by a telescope whose optical axis is approximately toroidal and views the puff with sight lines that are approximately normal to the
$1.5\ \mathrm {cm}$ beyond the outermost column of views, see figure 1, to puff a contrast gas into the boundary plasma. The line emission arising from the interaction between the gas atoms and the plasma are captured by a telescope whose optical axis is approximately toroidal and views the puff with sight lines that are approximately normal to the ![]() $(R,Z)$-plane at the toroidal angle of the nozzle. A fiber optic cable carries the light imaged by the telescope to a
$(R,Z)$-plane at the toroidal angle of the nozzle. A fiber optic cable carries the light imaged by the telescope to a ![]() $9\times 10$ array of APDs which sample it at
$9\times 10$ array of APDs which sample it at ![]() $2\ \mathrm {MHz}$ (Cziegler et al. Reference Cziegler, Terry, Hughes and LaBombard2010).
$2\ \mathrm {MHz}$ (Cziegler et al. Reference Cziegler, Terry, Hughes and LaBombard2010).
The line emission intensity is related to the electron density ![]() ${n_{e}}$ and temperature
${n_{e}}$ and temperature ![]() ${T_{e}}$ as
${T_{e}}$ as
Here, ![]() $n_0$ is the puffed neutral gas density,
$n_0$ is the puffed neutral gas density, ![]() ${n_{e}}$ is the electron density and
${n_{e}}$ is the electron density and ![]() ${T_{e}}$ is the electron temperature. The function
${T_{e}}$ is the electron temperature. The function ![]() $f$ parameterizes the ratio of the density of particles in the upper level of the radiative emission to the ground state density times the rate of decay of the upper level. As discussed in a review by Zweben et al. (Reference Zweben, Terry, Stotler and Maqueda2017),
$f$ parameterizes the ratio of the density of particles in the upper level of the radiative emission to the ground state density times the rate of decay of the upper level. As discussed in a review by Zweben et al. (Reference Zweben, Terry, Stotler and Maqueda2017), ![]() $f$ is handily parameterized by a power law dependence on the electron density and temperature for perturbations around values of
$f$ is handily parameterized by a power law dependence on the electron density and temperature for perturbations around values of ![]() ${\langle {n_{e}} \rangle }$ and
${\langle {n_{e}} \rangle }$ and ![]() ${\langle {T_{e}} \rangle }$ as
${\langle {T_{e}} \rangle }$ as ![]() $f({n_{e}}, {T_{e}}) \propto {n_{e}}^{\alpha } {T_{e}}^{\beta }$ where exponents
$f({n_{e}}, {T_{e}}) \propto {n_{e}}^{\alpha } {T_{e}}^{\beta }$ where exponents ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are specific to the neutral species used for the diagnostics and are anticipated to depend weakly on
$\beta$ are specific to the neutral species used for the diagnostics and are anticipated to depend weakly on ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ itself. Thus, for small relative fluctuations of
${T_{e}}$ itself. Thus, for small relative fluctuations of ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ one can assume
${T_{e}}$ one can assume ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ to be constant. For larger fluctuations, however, one needs to account for variations in the scaling exponents to correctly calculate
$\beta$ to be constant. For larger fluctuations, however, one needs to account for variations in the scaling exponents to correctly calculate ![]() $f$. This is further explained in the appendix. Typical values of the fluctuating plasma parameters in the Alcator C-Mod SOL are given by
$f$. This is further explained in the appendix. Typical values of the fluctuating plasma parameters in the Alcator C-Mod SOL are given by ![]() $5 \times 10^{18}\ \mathrm {m}^{-3} \lesssim {n_{e}} \lesssim 5 \times 10^{19}\ \mathrm {m}^{-3}$ and
$5 \times 10^{18}\ \mathrm {m}^{-3} \lesssim {n_{e}} \lesssim 5 \times 10^{19}\ \mathrm {m}^{-3}$ and ![]() $10\ \mathrm {eV} \lesssim {T_{e}} \lesssim 100\ \mathrm {eV}$ (LaBombard et al. Reference LaBombard, Goetz, Hutchinson, Jablonski, Kesner, Kurz, Lipschultz, McCracken, Niemczewski and Terry1997, Reference LaBombard, Boivin, Greenwald, Hughes, Lipschultz, Mossessian, Pitcher, Terry and Zweben2001, Reference LaBombard, Rice, Hubbard, Hughes, Greenwald, Irby, Lin, Lipschultz, Marmar and Pitcher2004; Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018b, Reference Kube, Garcia, Theodorsen, Kuang, LaBombard, Terry and Brunner2019).
$10\ \mathrm {eV} \lesssim {T_{e}} \lesssim 100\ \mathrm {eV}$ (LaBombard et al. Reference LaBombard, Goetz, Hutchinson, Jablonski, Kesner, Kurz, Lipschultz, McCracken, Niemczewski and Terry1997, Reference LaBombard, Boivin, Greenwald, Hughes, Lipschultz, Mossessian, Pitcher, Terry and Zweben2001, Reference LaBombard, Rice, Hubbard, Hughes, Greenwald, Irby, Lin, Lipschultz, Marmar and Pitcher2004; Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018b, Reference Kube, Garcia, Theodorsen, Kuang, LaBombard, Terry and Brunner2019).
For this parameter range the exponents for HeI are within the range ![]() $0.2 \lesssim \alpha \lesssim 0.8$ and
$0.2 \lesssim \alpha \lesssim 0.8$ and ![]() $-0.4 \lesssim \beta \lesssim 1.0$. Referring to figure 7 in Zweben et al. (Reference Zweben, Terry, Stotler and Maqueda2017) we note that in this parameter range
$-0.4 \lesssim \beta \lesssim 1.0$. Referring to figure 7 in Zweben et al. (Reference Zweben, Terry, Stotler and Maqueda2017) we note that in this parameter range ![]() $\alpha$ decreases monotonously with
$\alpha$ decreases monotonously with ![]() ${n_{e}}$ whereas it varies little with
${n_{e}}$ whereas it varies little with ![]() ${T_{e}}$ and that
${T_{e}}$ and that ![]() $\beta$ decreases monotonically with
$\beta$ decreases monotonically with ![]() ${T_{e}}$ whereas it varies little with
${T_{e}}$ whereas it varies little with ![]() ${n_{e}}$. Most importantly,
${n_{e}}$. Most importantly, ![]() $f$ is approximately linear in
$f$ is approximately linear in ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ for small
${T_{e}}$ for small ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ whereas
${T_{e}}$ whereas ![]() $f$ becomes less sensitive to
$f$ becomes less sensitive to ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ as they increase.
${T_{e}}$ as they increase.
Equation (2.1) relates the measured line emission intensity to the plasma parameters and is subject to several assumptions. First, the radiative decay rate needs to be faster than characteristic time scales of the plasma fluctuations, neutral particle transport and other atomic physics processes. For the HeI ![]() $587\ \mathrm {nm}$ line, the radiative decay rate is given by the Einstein coefficient
$587\ \mathrm {nm}$ line, the radiative decay rate is given by the Einstein coefficient ![]() $A \approx 2 \times 10^{7}\ \mathrm {s}^{-1}$, whereas the turbulence time scale is approximately
$A \approx 2 \times 10^{7}\ \mathrm {s}^{-1}$, whereas the turbulence time scale is approximately ![]() $10\ \mathrm {\mu } \mathrm {s}$. This shows that atomic processes have equilibrated on the turbulence time scales. Second,
$10\ \mathrm {\mu } \mathrm {s}$. This shows that atomic processes have equilibrated on the turbulence time scales. Second, ![]() $n_0$ is assumed to be slowly varying in time so that all fluctuations in
$n_0$ is assumed to be slowly varying in time so that all fluctuations in ![]() $I$ can be ascribed to fluctuations in
$I$ can be ascribed to fluctuations in ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$. This assumption is more questionable and will be discussed further in the next section.
${T_{e}}$. This assumption is more questionable and will be discussed further in the next section.
A synthetic line emission intensity signal is constructed using the emission rate ![]() $f$ for the
$f$ for the ![]() $587\ \mathrm {nm}$ line of HeI, as calculated by the DEGAS2 code (Stotler & Karney Reference Stotler and Karney1994). Interpolating
$587\ \mathrm {nm}$ line of HeI, as calculated by the DEGAS2 code (Stotler & Karney Reference Stotler and Karney1994). Interpolating ![]() $f$ for the instantaneous
$f$ for the instantaneous ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ measurements reported by the MLP we calculate
${T_{e}}$ measurements reported by the MLP we calculate
Note that by using interpolated values of ![]() $f$ we avoid using the scaling exponents
$f$ we avoid using the scaling exponents ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ in the calculation of
$\beta$ in the calculation of ![]() ${I_\textrm {syn}}$. Figure 2 illustrates the dependence of
${I_\textrm {syn}}$. Figure 2 illustrates the dependence of ![]() ${I_\textrm {syn}}$ on
${I_\textrm {syn}}$ on ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$. Also shown are
${T_{e}}$. Also shown are ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ values reported by the MLP in the discharges discussed in this paper. This figure is further discussed in § 3. Comparing this expression to (2.1), we note that the puffed-gas density
${T_{e}}$ values reported by the MLP in the discharges discussed in this paper. This figure is further discussed in § 3. Comparing this expression to (2.1), we note that the puffed-gas density ![]() $n_0$ is assumed to be constant and absorbed into
$n_0$ is assumed to be constant and absorbed into ![]() ${I_\textrm {syn}}$. This method for constructing synthetic GPI emissions is also used by Stotler et al. (Reference Stotler, LaBombard, Terry and Zweben2003) and Halpern et al. (Reference Halpern, Terry, Zweben, LaBombard, Podesta and Ricci2015). We further note here that a recently developed line-ratio spectroscopy diagnostic that has been implemented at the ASDEX Upgrade tokamak allows
${I_\textrm {syn}}$. This method for constructing synthetic GPI emissions is also used by Stotler et al. (Reference Stotler, LaBombard, Terry and Zweben2003) and Halpern et al. (Reference Halpern, Terry, Zweben, LaBombard, Podesta and Ricci2015). We further note here that a recently developed line-ratio spectroscopy diagnostic that has been implemented at the ASDEX Upgrade tokamak allows ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ to be measured directly using information from multiple He line emission in combination with state-of-the-art collisional-radiative models (Muñoz Burgos et al. Reference Muñoz Burgos, Schmitz, Loch and Ballance2012; Griener et al. Reference Griener, Burgos, Cavedon, Birkenmeier, Dux, Kurzan, Schmitz, Sieglin, Stroth and Viezzer2017a,Reference Griener, Schmitz, Bald, Bösser, Cavedon, De Marné, Eich, Fuchert, Herrmann and Kappatoub)
${T_{e}}$ to be measured directly using information from multiple He line emission in combination with state-of-the-art collisional-radiative models (Muñoz Burgos et al. Reference Muñoz Burgos, Schmitz, Loch and Ballance2012; Griener et al. Reference Griener, Burgos, Cavedon, Birkenmeier, Dux, Kurzan, Schmitz, Sieglin, Stroth and Viezzer2017a,Reference Griener, Schmitz, Bald, Bösser, Cavedon, De Marné, Eich, Fuchert, Herrmann and Kappatoub)

Figure 2. Synthetic emission rate for the HeI ![]() $587\ \mathrm {nm}$ line as a function of the electron density and temperature. Overplotted are the average
$587\ \mathrm {nm}$ line as a function of the electron density and temperature. Overplotted are the average ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ values reported by the MLP at different
${T_{e}}$ values reported by the MLP at different ![]() $\rho$ positions in discharge 1 (black markers) and 2 (white markers). The error bars are given by the respective root-mean-square values.
$\rho$ positions in discharge 1 (black markers) and 2 (white markers). The error bars are given by the respective root-mean-square values.
2.2. Calculation of profiles
The fluctuations of the plasma parameters can be characterized by their lower order statistical moments, that is, the mean, standard deviation, skewness and excess kurtosis. Scanning the Langmuir probe through the SOL yields a set of ![]() ${I_{s}}$,
${I_{s}}$, ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ samples within a given radial interval along the scan path. Here
${T_{e}}$ samples within a given radial interval along the scan path. Here ![]() ${I_{s}}$ is the ion saturation current. The center of the sampled interval is then mapped to the outboard mid-plane and assigned a
${I_{s}}$ is the ion saturation current. The center of the sampled interval is then mapped to the outboard mid-plane and assigned a ![]() $\rho _\mathrm {mid}$ value, corresponding to the distance from the LCFS. The number of samples within a given interval depends on the velocity with which the probe moves through the SOL as well as the width chosen for the sampling interval. Here, we use only data from the last two probe scans of discharge
$\rho _\mathrm {mid}$ value, corresponding to the distance from the LCFS. The number of samples within a given interval depends on the velocity with which the probe moves through the SOL as well as the width chosen for the sampling interval. Here, we use only data from the last two probe scans of discharge ![]() $1$ and
$1$ and ![]() $2$, as to sample data when the plasma SOL was stable in space and time.
$2$, as to sample data when the plasma SOL was stable in space and time.
The ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ data reported by the MLP are partitioned into separate sets for each instance, where the probe is within
${T_{e}}$ data reported by the MLP are partitioned into separate sets for each instance, where the probe is within ![]() $\rho _{\mathrm {mid}} \pm \triangle _\rho$, that is, individually for the inward and outward part motion and individually for each probe plunge. Thus, for two probe plunges there are four datasets for
$\rho _{\mathrm {mid}} \pm \triangle _\rho$, that is, individually for the inward and outward part motion and individually for each probe plunge. Thus, for two probe plunges there are four datasets for ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$, respectively. The lowest-order statistical moments are calculated from the union of these data sets. To estimate the probability distribution function, the data time series are normalized by subtracting their sample mean and scaling with their respective root-mean-square value. This procedure was chosen to account for variations in the SOL plasma on a time scale comparable with the probe reciprocation time scale and the delay between consecutive probe plunges. Radial profiles of the lowest-order statistical moments of the GPI data can be calculated using the time series of signals from the individual views.
${T_{e}}$, respectively. The lowest-order statistical moments are calculated from the union of these data sets. To estimate the probability distribution function, the data time series are normalized by subtracting their sample mean and scaling with their respective root-mean-square value. This procedure was chosen to account for variations in the SOL plasma on a time scale comparable with the probe reciprocation time scale and the delay between consecutive probe plunges. Radial profiles of the lowest-order statistical moments of the GPI data can be calculated using the time series of signals from the individual views.
Skewness ![]() $S$ and excess kurtosis or flatness,
$S$ and excess kurtosis or flatness, ![]() $F$, of a data sample are invariant under linear transformations. In order to remove low-frequency trends in the data time series, for example, owing to shifts in the position of the LCFS,
$F$, of a data sample are invariant under linear transformations. In order to remove low-frequency trends in the data time series, for example, owing to shifts in the position of the LCFS, ![]() $S$ and
$S$ and ![]() $F$ are calculated after normalizing the data samples according to
$F$ are calculated after normalizing the data samples according to
Here ![]() ${\langle \varPhi \rangle }_\mathrm {mv}$ denotes a moving average and
${\langle \varPhi \rangle }_\mathrm {mv}$ denotes a moving average and ![]() $\varPhi _\mathrm {rms}$ the moving root-mean-square value. Both are calculated using a moving window of approximately 4 ms. This common normalization allows the statistical properties of the fluctuations around the mean to be compared for different data time series using different diagnostic techniques. In the remainder of this article, all data time series are normalized according to (2.3).
$\varPhi _\mathrm {rms}$ the moving root-mean-square value. Both are calculated using a moving window of approximately 4 ms. This common normalization allows the statistical properties of the fluctuations around the mean to be compared for different data time series using different diagnostic techniques. In the remainder of this article, all data time series are normalized according to (2.3).
2.3. Parameter estimation
It has been shown previously that measurement time series of the SOL plasma can be modelled accurately as a superposition of uncorrelated, two-sided exponential pulses. In the following, we discuss how the intermittency parameter ![]() $\gamma$, the pulse duration time
$\gamma$, the pulse duration time ![]() ${\tau _{d}}$, the pulse asymmetry parameter
${\tau _{d}}$, the pulse asymmetry parameter ![]() $\lambda$ and the average waiting time between two consecutive pulses
$\lambda$ and the average waiting time between two consecutive pulses ![]() ${\langle {\tau _{w}} \rangle }$ are reliably estimated from measurement data.
${\langle {\tau _{w}} \rangle }$ are reliably estimated from measurement data.
We obtain the intermittency parameter ![]() $\gamma$ by fitting equation (A9) in Theodorsen et al. (Reference Theodorsen, Garcia and Rypdal2017b) on the histogram of the measured time-series data, minimizing the logarithm of the squared residuals.
$\gamma$ by fitting equation (A9) in Theodorsen et al. (Reference Theodorsen, Garcia and Rypdal2017b) on the histogram of the measured time-series data, minimizing the logarithm of the squared residuals.
The PSD for a time series that results from a superposition of uncorrelated exponential pulses is given by (Garcia & Theodorsen Reference Garcia and Theodorsen2017)
Here ![]() ${\tau _{d}}$ denotes the pulse duration time and
${\tau _{d}}$ denotes the pulse duration time and ![]() $\lambda$ denotes the pulse asymmetry. The e-folding time of the pulse rise is then given by
$\lambda$ denotes the pulse asymmetry. The e-folding time of the pulse rise is then given by ![]() $\lambda {\tau _{d}}$ and the e-folding time of the pulse decay is given by
$\lambda {\tau _{d}}$ and the e-folding time of the pulse decay is given by ![]() $(1 - \lambda ) {\tau _{d}}$. We note that the PSD of the entire signal is the same as the PSD of a single pulse. The PSD has a Lorentzian shape, featuring a flat part for low frequencies and a power-law decay for high frequencies. The point of transition between these two regions is parameterized by
$(1 - \lambda ) {\tau _{d}}$. We note that the PSD of the entire signal is the same as the PSD of a single pulse. The PSD has a Lorentzian shape, featuring a flat part for low frequencies and a power-law decay for high frequencies. The point of transition between these two regions is parameterized by ![]() ${\tau _{d}}$ and the width of the transition region is given by
${\tau _{d}}$ and the width of the transition region is given by ![]() $\lambda$. Note that for very small values of
$\lambda$. Note that for very small values of ![]() $\lambda$ the power law scaling can be further divided into a region where the PSD decays quadratically and into a region where the PSD decays as
$\lambda$ the power law scaling can be further divided into a region where the PSD decays quadratically and into a region where the PSD decays as ![]() $( {\tau _{d}} \omega )^{-4}$ (Garcia & Theodorsen Reference Garcia and Theodorsen2017). For the data at hand, PSDs are calculated using Welch's method. This requires long data time series, which excludes data from scanning MLP operation.
$( {\tau _{d}} \omega )^{-4}$ (Garcia & Theodorsen Reference Garcia and Theodorsen2017). For the data at hand, PSDs are calculated using Welch's method. This requires long data time series, which excludes data from scanning MLP operation.
Data from the MLP are pre-processed by convolving it with a 12-point boxcar window, that is a rectangular modulation of the signal (LaBombard & Lyons Reference LaBombard and Lyons2007). Assuming that the pulse shapes in the time series of plasma parameters are well described by a two-sided exponential function, the MLP registers such pulses as just this pulse shape filtered with a boxcar window. As the PSD of a superposition of uncorrelated pulses, i.e., the time series of the plasma parameters, is given by the PSD of an individual pulse (Garcia & Theodorsen Reference Garcia and Theodorsen2017), the expected power spectrum of MLP data time series is given by the product of (2.4) and the Fourier transformation of a boxcar window:
Note that this expression holds for raw signals, not for signals normalized according to (2.3). To estimate the duration time ![]() ${\tau _{d}}$ and pulse asymmetry parameter
${\tau _{d}}$ and pulse asymmetry parameter ![]() $\lambda$, (2.4) is used to fit the GPI data and (2.5) is used to fit the MLP data.
$\lambda$, (2.4) is used to fit the GPI data and (2.5) is used to fit the MLP data.
In order to obtain precise waiting time statistics and the a best estimate of ![]() ${\tau _{w}}$, a method based on Richardson–Lucy (RL) deconvolution is used (Richardson Reference Richardson1972; Lucy Reference Lucy1974). This method was previously used for a comparison of GPI data from several different confinement modes in Alcator C-Mod. The method is described in more detail by Theodorsen et al. (Reference Theodorsen, Garcia, Kube, LaBombard and Terry2018), here we briefly describe the deconvolution.
${\tau _{w}}$, a method based on Richardson–Lucy (RL) deconvolution is used (Richardson Reference Richardson1972; Lucy Reference Lucy1974). This method was previously used for a comparison of GPI data from several different confinement modes in Alcator C-Mod. The method is described in more detail by Theodorsen et al. (Reference Theodorsen, Garcia, Kube, LaBombard and Terry2018), here we briefly describe the deconvolution.
By assuming that the dwell MLP and single-diode GPI signals are comprised by a series of uncorrelated pulses with a common pulse shape ![]() $\phi$ and a fixed duration
$\phi$ and a fixed duration ![]() ${\tau _{d}}$, the signals can be written as a convolution between the pulse shape and a forcing given by a train of delta pulses,
${\tau _{d}}$, the signals can be written as a convolution between the pulse shape and a forcing given by a train of delta pulses,
where
 \begin{equation} F(t) = \sum_{k=1}^{K(T)} A_k \delta\left(\frac{t-t_k}{{\tau_{d}}}\right). \end{equation}
\begin{equation} F(t) = \sum_{k=1}^{K(T)} A_k \delta\left(\frac{t-t_k}{{\tau_{d}}}\right). \end{equation}
The signal ![]() $\varPhi$ can be seen as a train of delta pulses arriving according to a Poisson process
$\varPhi$ can be seen as a train of delta pulses arriving according to a Poisson process ![]() $F$, passed through a filter
$F$, passed through a filter ![]() $\phi$. It is therefore called a filtered Poisson process (FPP). For a prescribed pulse shape
$\phi$. It is therefore called a filtered Poisson process (FPP). For a prescribed pulse shape ![]() $\phi$ and a time series measurement of
$\phi$ and a time series measurement of ![]() $\varPhi$, the RL deconvolution can be used to estimate
$\varPhi$, the RL deconvolution can be used to estimate ![]() $F$, that is, the pulse amplitudes
$F$, that is, the pulse amplitudes ![]() $A_k$ and arrival times
$A_k$ and arrival times ![]() $t_k$. From the estimated forcing
$t_k$. From the estimated forcing ![]() $F$, the waiting time statistics can be extracted. The RL deconvolution is a point-wise iterative procedure that is known to converge to the least-squares solution (Dell'Acqua et al. Reference Dell'Acqua, Rizzo, Scifo, Clarke, Scotti and Fazio2007). For measurements with normally distributed measurement noise, the
$F$, the waiting time statistics can be extracted. The RL deconvolution is a point-wise iterative procedure that is known to converge to the least-squares solution (Dell'Acqua et al. Reference Dell'Acqua, Rizzo, Scifo, Clarke, Scotti and Fazio2007). For measurements with normally distributed measurement noise, the ![]() $n+1$th iteration is given by (Daube-Witherspoon & Muehllehner Reference Daube-Witherspoon and Muehllehner1986; Pruksch & Fleischmann Reference Pruksch, Fleischmann, Albrecht, Hook and Bushouse1998; Dell'Acqua et al. Reference Dell'Acqua, Rizzo, Scifo, Clarke, Scotti and Fazio2007; Tai, Tan & Brown Reference Tai, Tan and Brown2011)
$n+1$th iteration is given by (Daube-Witherspoon & Muehllehner Reference Daube-Witherspoon and Muehllehner1986; Pruksch & Fleischmann Reference Pruksch, Fleischmann, Albrecht, Hook and Bushouse1998; Dell'Acqua et al. Reference Dell'Acqua, Rizzo, Scifo, Clarke, Scotti and Fazio2007; Tai, Tan & Brown Reference Tai, Tan and Brown2011)
 \begin{equation} F^{(n+1)}(t) = F^{(n)}(t) \frac{[\varPhi * \hat{\phi}](t)}{[F^{(n)} * \phi * \hat{\phi}](t)}, \end{equation}
\begin{equation} F^{(n+1)}(t) = F^{(n)}(t) \frac{[\varPhi * \hat{\phi}](t)}{[F^{(n)} * \phi * \hat{\phi}](t)}, \end{equation}
where ![]() $\hat {\phi }(t) = \phi (-t)$. For non-negative
$\hat {\phi }(t) = \phi (-t)$. For non-negative ![]() $\varPhi$ and
$\varPhi$ and ![]() $f^{(0)}$, each following iteration will be non-negative as well. The initial choice
$f^{(0)}$, each following iteration will be non-negative as well. The initial choice ![]() $f^{(0)}$ is otherwise unimportant, and has here been set at constant unity. For consistency with PSD estimates of
$f^{(0)}$ is otherwise unimportant, and has here been set at constant unity. For consistency with PSD estimates of ![]() ${\tau _{d}}$ and
${\tau _{d}}$ and ![]() $\lambda$ (see § 3), we use a two-sided exponential pulse function with
$\lambda$ (see § 3), we use a two-sided exponential pulse function with ![]() ${\tau _{d}} = 20\ \mathrm {\mu } \text {s}$ and
${\tau _{d}} = 20\ \mathrm {\mu } \text {s}$ and ![]() $\lambda = 1/10$ for the GPI data, and a two-sided exponential pulse function with
$\lambda = 1/10$ for the GPI data, and a two-sided exponential pulse function with ![]() ${\tau _{d}}=10\ \mathrm {\mu }\text {s}$ and
${\tau _{d}}=10\ \mathrm {\mu }\text {s}$ and ![]() $\lambda = 1/25$ convolved with the 12-point window for the MLP data. The deconvolution procedure is robust to small deviations in the pulse shape.
$\lambda = 1/25$ convolved with the 12-point window for the MLP data. The deconvolution procedure is robust to small deviations in the pulse shape.
The deconvolution algorithm was run for ![]() $10^5$ iterations, after which the
$10^5$ iterations, after which the ![]() $L^2$-norm of the difference between the measured time series and the reconstructed time series was considered sufficiently small. The result of the deconvolution resembles a series of sharply localized, Gaussian pulses, so a peak-finding algorithm is employed in order to extract pulse arrival times and amplitudes from the deconvolved signal. The window size of the peak-finding algorithm is chosen to give the best fit to the expected number of events in the time series, resulting in window sizes of
$L^2$-norm of the difference between the measured time series and the reconstructed time series was considered sufficiently small. The result of the deconvolution resembles a series of sharply localized, Gaussian pulses, so a peak-finding algorithm is employed in order to extract pulse arrival times and amplitudes from the deconvolved signal. The window size of the peak-finding algorithm is chosen to give the best fit to the expected number of events in the time series, resulting in window sizes of ![]() $7.5\ \mathrm {\mu } \mathrm {s}$ (I s),
$7.5\ \mathrm {\mu } \mathrm {s}$ (I s), ![]() $0.9\ \mathrm {\mu } \text {s}$ (n e),
$0.9\ \mathrm {\mu } \text {s}$ (n e), ![]() $6.3\ \mathrm {\mu } \text {s}$ (T e),
$6.3\ \mathrm {\mu } \text {s}$ (T e), ![]() $4.5\ \mathrm {\mu } \text {s}$ (GPI, for the view at
$4.5\ \mathrm {\mu } \text {s}$ (GPI, for the view at ![]() $90.7\ \text {cm}$) and
$90.7\ \text {cm}$) and ![]() $7.5\ \mathrm {\mu } \text {s}$ (GPI, for the view at
$7.5\ \mathrm {\mu } \text {s}$ (GPI, for the view at ![]() $91 \ \text {cm}$). The deconvolution procedure finds
$91 \ \text {cm}$). The deconvolution procedure finds ![]() $85\,001$,
$85\,001$, ![]() $200\,332$,
$200\,332$, ![]() $101\,815$,
$101\,815$, ![]() $30\,574$ and
$30\,574$ and ![]() $17\,343$ pulses in these time series, respectively.
$17\,343$ pulses in these time series, respectively.
In order to test the fidelity of the process, a synthetic time series consisting of a pure FPP has been subjected to the deconvolution procedure as well. This time series has the same sampling time, ![]() ${\tau _{d}}$ and
${\tau _{d}}$ and ![]() $\lambda$ as the GPI time series, with
$\lambda$ as the GPI time series, with ![]() $\gamma =2$. In this case, a window of
$\gamma =2$. In this case, a window of ![]() $5.5\ \mathrm {\mu } \text {s}$ gives the best fit to the expected number of events and the procedure finds 48 011 events (the true number of events in the synthetic time series is 50 000).
$5.5\ \mathrm {\mu } \text {s}$ gives the best fit to the expected number of events and the procedure finds 48 011 events (the true number of events in the synthetic time series is 50 000).
Example excerpts of the reconstructed time series are presented in figures 3 and 4. In both figures, the blue lines give the original time series, normalized according to (2.3). The green dots indicate the pulse arrival times and amplitudes that are the output of the deconvolution procedure described previously. The amplitudes have been normalized by their own mean value and standard deviation. By convolving the estimated train of delta pulses with the pulse shape, the full time series is reconstructed. The result of this reconstruction is given by the orange lines. Overall, the reconstruction is excellent. This shows that the deconvolution method can be used to reliably estimate ![]() ${\langle A \rangle }$ and
${\langle A \rangle }$ and ![]() ${\langle {\tau _{w}} \rangle }$ from a given realization of the process or from measurements.
${\langle {\tau _{w}} \rangle }$ from a given realization of the process or from measurements.

Figure 3. Excerpt of original (as measured by the MLP) and reconstructed T e signals. The blue curve gives the original signal T e, the green dots indicate arrival times ![]() $t_k$ and normalized amplitudes for the pulses
$t_k$ and normalized amplitudes for the pulses ![]() $A_k$ and the orange curve gives the reconstructed signal
$A_k$ and the orange curve gives the reconstructed signal ![]() $D$. All signals are normalized so as to have zero mean and unit standard deviation.
$D$. All signals are normalized so as to have zero mean and unit standard deviation.

Figure 4. Excerpt of original and reconstructed GPI signals at ![]() $R=91\ \text {cm}$. The blue curve gives the original signal
$R=91\ \text {cm}$. The blue curve gives the original signal ![]() $I_\mathrm {GPI}$, the green dots indicate arrival times
$I_\mathrm {GPI}$, the green dots indicate arrival times ![]() $t_k$ and normalized amplitudes
$t_k$ and normalized amplitudes ![]() $A_k$ for the pulses and the orange curve gives the reconstructed signal
$A_k$ for the pulses and the orange curve gives the reconstructed signal ![]() $D$. All signals are normalized so as to have zero mean and unit standard deviation.
$D$. All signals are normalized so as to have zero mean and unit standard deviation.
3. Results
3.1. Profiles of MLP, GPI and synthetic GPI data
Synthetic GPI emission rates are calculated according to (2.2). Discharge 1 features a SOL that is colder and less dense than the SOL plasma in discharge 2. Furthermore, the gradient scale lengths of the ![]() ${\langle {n_{e}} \rangle }$ and
${\langle {n_{e}} \rangle }$ and ![]() ${\langle {T_{e}} \rangle }$ profiles are shorter in discharge 1 (Kube et al. Reference Kube, Garcia, Theodorsen, Kuang, LaBombard, Terry and Brunner2019). Thus, the range of reported
${\langle {T_{e}} \rangle }$ profiles are shorter in discharge 1 (Kube et al. Reference Kube, Garcia, Theodorsen, Kuang, LaBombard, Terry and Brunner2019). Thus, the range of reported ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ values in discharge 1, shown by black markers in figure 2, is larger than the range reported in discharge 2 (white markers). The contour lines suggest that both
${T_{e}}$ values in discharge 1, shown by black markers in figure 2, is larger than the range reported in discharge 2 (white markers). The contour lines suggest that both ![]() $\partial \ln {I_\textrm {syn}} / \partial \ln {T_{e}}$ and
$\partial \ln {I_\textrm {syn}} / \partial \ln {T_{e}}$ and ![]() $\partial \ln {I_\textrm {syn}} / \partial \ln {n_{e}}$ are larger over the parameter range relevant for discharge 1 than they are for discharge 2. Consequently, variations in the amplitude of the plasma parameters
$\partial \ln {I_\textrm {syn}} / \partial \ln {n_{e}}$ are larger over the parameter range relevant for discharge 1 than they are for discharge 2. Consequently, variations in the amplitude of the plasma parameters ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ are mapped in a nonlinear way to variations in the amplitude of
${T_{e}}$ are mapped in a nonlinear way to variations in the amplitude of ![]() ${I_\textrm {syn}}$ and the local fluctuation exponents
${I_\textrm {syn}}$ and the local fluctuation exponents ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ cannot be used. Appendix A gives a more detailed discussion regarding the local exponent approximation.
$\beta$ cannot be used. Appendix A gives a more detailed discussion regarding the local exponent approximation.
We now compare the lowest-order statistical moments of the different signals. Figure 5 shows radial profiles of the mean, the relative fluctuation level, skewness and intermittency parameter for the relevant MLP data (![]() ${n_{e}}$,
${n_{e}}$, ![]() ${T_{e}}$ and
${T_{e}}$ and ![]() ${I_{s}}$), the GPI data, as well as the synthetic GPI data (
${I_{s}}$), the GPI data, as well as the synthetic GPI data (![]() ${I_\textrm {syn}}$). Looking at the profile of the average values of
${I_\textrm {syn}}$). Looking at the profile of the average values of ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$, shown in 5(a) we note that the scale lengths of both quantities are almost identical. Both
${T_{e}}$, shown in 5(a) we note that the scale lengths of both quantities are almost identical. Both ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ decay sharply for
${T_{e}}$ decay sharply for ![]() $\rho \lesssim 1\ \mathrm {cm}$. With larger distance from the LCFS their profiles feature a larger scale length. GPI data feature a relative fluctuation level between
$\rho \lesssim 1\ \mathrm {cm}$. With larger distance from the LCFS their profiles feature a larger scale length. GPI data feature a relative fluctuation level between ![]() $0.2$ close to the separatrix and larger than
$0.2$ close to the separatrix and larger than ![]() $0.6$ close to limiter shadow. The MLP data show relative fluctuation levels in the range between approximately
$0.6$ close to limiter shadow. The MLP data show relative fluctuation levels in the range between approximately ![]() $0.2$ and
$0.2$ and ![]() $0.4$. Both MLP and GPI data feature a fluctuation level of up to
$0.4$. Both MLP and GPI data feature a fluctuation level of up to ![]() $0.5$ times their respective mean. This relative fluctuation level increases with distance from the LCFS. The relative fluctuation level of the
$0.5$ times their respective mean. This relative fluctuation level increases with distance from the LCFS. The relative fluctuation level of the ![]() ${I_\textrm {syn}}$ data also increases with
${I_\textrm {syn}}$ data also increases with ![]() $\rho$ but is less than the fluctuation level of the GPI data (by factors of
$\rho$ but is less than the fluctuation level of the GPI data (by factors of ![]() ${\sim }0.85$ and
${\sim }0.85$ and ![]() ${\sim }0.3$) over the profile. Coefficients of sample skewness for the MLP and the GPI data are positive, comparable in magnitude and increase with
${\sim }0.3$) over the profile. Coefficients of sample skewness for the MLP and the GPI data are positive, comparable in magnitude and increase with ![]() $\rho$. The synthetic data features negative sample skewness for
$\rho$. The synthetic data features negative sample skewness for ![]() $\rho \lesssim 1\ \mathrm {cm}$ but are positive and increasing for
$\rho \lesssim 1\ \mathrm {cm}$ but are positive and increasing for ![]() $\rho \gtrsim 1\ \mathrm {cm}$. For both MLP and GPI data,
$\rho \gtrsim 1\ \mathrm {cm}$. For both MLP and GPI data, ![]() $F$ increases from approximately
$F$ increases from approximately ![]() $0$ at
$0$ at ![]() $\rho \approx 0.5\ \mathrm {cm}$ to larger positive values for
$\rho \approx 0.5\ \mathrm {cm}$ to larger positive values for ![]() $\rho \approx 1.5\ \mathrm {cm}$.
$\rho \approx 1.5\ \mathrm {cm}$. ![]() $F$ calculated using
$F$ calculated using ![]() ${I_\textrm {syn}}$ data is approximately zero over the entire range of
${I_\textrm {syn}}$ data is approximately zero over the entire range of ![]() $\rho$. The lowest panel of figure 5 shows the intermittency parameter
$\rho$. The lowest panel of figure 5 shows the intermittency parameter ![]() $\gamma$, obtained by a fit on the histogram of data sampled in a given
$\gamma$, obtained by a fit on the histogram of data sampled in a given ![]() $\rho$ bin. Both, MLP and GPI data feature a large value of
$\rho$ bin. Both, MLP and GPI data feature a large value of ![]() $\gamma \gtrsim 10$ for
$\gamma \gtrsim 10$ for ![]() $\rho \lesssim 1\ \mathrm {cm}$. This implies that the probability density functions (PDFs) closely follow a normal distribution, which is consistent with small values of
$\rho \lesssim 1\ \mathrm {cm}$. This implies that the probability density functions (PDFs) closely follow a normal distribution, which is consistent with small values of ![]() $S$ and
$S$ and ![]() $F$. For larger
$F$. For larger ![]() $\rho$ values the data features positively skewed and flattened histograms, a feature captured by the smaller
$\rho$ values the data features positively skewed and flattened histograms, a feature captured by the smaller ![]() $\gamma$ value and compatible with the larger estimates of
$\gamma$ value and compatible with the larger estimates of ![]() $S$ and
$S$ and ![]() $F$. For the synthetic data,
$F$. For the synthetic data, ![]() $\gamma$ is estimated to be larger than
$\gamma$ is estimated to be larger than ![]() $10$ over the entire range of
$10$ over the entire range of ![]() $\rho$. This implies that these samples closely follow a normal distribution, which is compatible with nearly vanishing skewness and excess kurtosis of this data. Although the radial profiles of the lowest-order statistical moments calculated using MLP and GPI data agree qualitatively, the profiles of the
$\rho$. This implies that these samples closely follow a normal distribution, which is compatible with nearly vanishing skewness and excess kurtosis of this data. Although the radial profiles of the lowest-order statistical moments calculated using MLP and GPI data agree qualitatively, the profiles of the ![]() ${I_\textrm {syn}}$ data show large discrepancies. The relative fluctuation level of the
${I_\textrm {syn}}$ data show large discrepancies. The relative fluctuation level of the ![]() ${I_\textrm {syn}}$ data is comparable with the relative fluctuation level of the
${I_\textrm {syn}}$ data is comparable with the relative fluctuation level of the ![]() ${I_{s}}$,
${I_{s}}$, ![]() ${n_{e}}$,
${n_{e}}$, ![]() ${T_{e}}$ and the GPI data, whereas
${T_{e}}$ and the GPI data, whereas ![]() $S$,
$S$, ![]() $F$ and
$F$ and ![]() $\gamma$ calculated using
$\gamma$ calculated using ![]() ${I_\textrm {syn}}$ data correspond to a near-Gaussian process. Figure 6 shows
${I_\textrm {syn}}$ data correspond to a near-Gaussian process. Figure 6 shows ![]() ${n_{e}}$,
${n_{e}}$, ![]() ${T_{e}}$ and
${T_{e}}$ and ![]() ${I_\textrm {syn}}$ time series. The waveforms of the
${I_\textrm {syn}}$ time series. The waveforms of the ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ data present intermittent and asymmetric large-amplitude bursts for both discharge 1 and 2. Peaks in the
${T_{e}}$ data present intermittent and asymmetric large-amplitude bursts for both discharge 1 and 2. Peaks in the ![]() ${I_\textrm {syn}}$, on the other hand,appear with a somewhat smaller amplitude relative to the quiet time between bursts and with a more symmetric shape. Histograms of the corresponding data, shown in figure 7, corroborate this interpretation. For the data sampled in discharge 1 (full lines in figure 6 and the left panel in figure 7), histograms of the
${I_\textrm {syn}}$, on the other hand,appear with a somewhat smaller amplitude relative to the quiet time between bursts and with a more symmetric shape. Histograms of the corresponding data, shown in figure 7, corroborate this interpretation. For the data sampled in discharge 1 (full lines in figure 6 and the left panel in figure 7), histograms of the ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ data are asymmetric with elevated tails for large-amplitude events. The histogram of the
${T_{e}}$ data are asymmetric with elevated tails for large-amplitude events. The histogram of the ![]() ${I_\textrm {syn}}$ data, on the other hand, features no elevated tail for large-amplitude events. For
${I_\textrm {syn}}$ data, on the other hand, features no elevated tail for large-amplitude events. For ![]() $\tilde {I}_\mathrm {syn} \gtrsim 2.5$ the histogram is approximately zero. For discharge 2 (dashed lines in figure 6 and the right panel in figure 7), the histogram of the
$\tilde {I}_\mathrm {syn} \gtrsim 2.5$ the histogram is approximately zero. For discharge 2 (dashed lines in figure 6 and the right panel in figure 7), the histogram of the ![]() ${I_\textrm {syn}}$ data appears symmetric and features a plateau around
${I_\textrm {syn}}$ data appears symmetric and features a plateau around ![]() $\tilde {I}_\mathrm {syn} = 0$ without a pronounced peak.
$\tilde {I}_\mathrm {syn} = 0$ without a pronounced peak.

Figure 5. Radial profiles of various quantities sampled in discharge 1: (a) average; (b) relative fluctuation level; (c) skewness; (d) relative fluctuation level; and (e) intermittency parameter. The colour legend in (e) applies to all subplots.

Figure 6. Time series of ![]() ${n_{e}}$ (lowest panel),
${n_{e}}$ (lowest panel), ![]() ${T_{e}}$ (middle panel) and synthetic GPI data (top panel) for discharge 1 (full line) and 2 (dashed line). Data are taken in the first interval where the probe scans from
${T_{e}}$ (middle panel) and synthetic GPI data (top panel) for discharge 1 (full line) and 2 (dashed line). Data are taken in the first interval where the probe scans from ![]() $\rho = 1.3$ to
$\rho = 1.3$ to ![]() $1.2\ \mathrm {cm}$.
$1.2\ \mathrm {cm}$.

Figure 7. Histogram of ![]() $\tilde {n}_{e}$ (blue dots),
$\tilde {n}_{e}$ (blue dots), ![]() $\tilde {T}_{e}$ (orange dots) and
$\tilde {T}_{e}$ (orange dots) and ![]() $\tilde {I}_\mathrm {syn}$ (purple dots) for discharge 1 (left) and 2 (right). Data are taken in all intervals where the probe scans from
$\tilde {I}_\mathrm {syn}$ (purple dots) for discharge 1 (left) and 2 (right). Data are taken in all intervals where the probe scans from ![]() $\rho = 1.2$ to
$\rho = 1.2$ to ![]() $1.3\ \mathrm {cm}$.
$1.3\ \mathrm {cm}$.
The different fluctuation statistics can be understood by referring to figure 2. For one, ![]() ${I_\textrm {syn}}$ is more sensitive to
${I_\textrm {syn}}$ is more sensitive to ![]() ${T_{e}}$ fluctuations than to
${T_{e}}$ fluctuations than to ![]() ${n_{e}}$ fluctuations, that is,
${n_{e}}$ fluctuations, that is, ![]() $\partial {I_\textrm {syn}} / \partial {T_{e}} > \partial {I_\textrm {syn}} / \partial {n_{e}}$ within relevant ranges of
$\partial {I_\textrm {syn}} / \partial {T_{e}} > \partial {I_\textrm {syn}} / \partial {n_{e}}$ within relevant ranges of ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$. Fluctuations in
${T_{e}}$. Fluctuations in ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ are strongly correlated and feature similar exponential pulse shapes (Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018b). These are similar to experimentally measured GPI exponential pulse shapes (Garcia Reference Garcia2012; Garcia et al. Reference Garcia, Fritzner, Kube, Cziegler, LaBombard and Terry2013b). However, (2.2) will not result in a perfectly scaled pulse shape of the input signals because it depends nonlinearly on both
${T_{e}}$ are strongly correlated and feature similar exponential pulse shapes (Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018b). These are similar to experimentally measured GPI exponential pulse shapes (Garcia Reference Garcia2012; Garcia et al. Reference Garcia, Fritzner, Kube, Cziegler, LaBombard and Terry2013b). However, (2.2) will not result in a perfectly scaled pulse shape of the input signals because it depends nonlinearly on both ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$.
${T_{e}}$.
3.2. Statistical properties of MLP and GPI data
In the following, we present a statistical analysis of measurements taken from the dwelled MLP in discharge 3. These are compared with GPI data taken from two diode view positions, one radially slightly inside and one slightly outside of the estimated MLP position.
Figure 8 shows the frequency PSDs calculated from MLP and GPI data sampled in discharge 3. The PSDs of the GPI data from the two different radial positions, shown in the left panel, are almost identical. They are flat for low frequencies, ![]() $f \lesssim 5\ \mathrm {kHz}$, before transitioning into a broken power law decay for high frequencies. A least-squares fit of (2.4) on the data (black line) yields
$f \lesssim 5\ \mathrm {kHz}$, before transitioning into a broken power law decay for high frequencies. A least-squares fit of (2.4) on the data (black line) yields ![]() ${\tau _{d}} \approx 20\ \mathrm {\mu } \mathrm {s}$ and
${\tau _{d}} \approx 20\ \mathrm {\mu } \mathrm {s}$ and ![]() $\lambda \approx 0.1$ and describes the PSDs of the signals perfectly over more than four decades.
$\lambda \approx 0.1$ and describes the PSDs of the signals perfectly over more than four decades.
PSDs of the MLP data (![]() ${I_{s}}$,
${I_{s}}$, ![]() ${n_{e}}$, and
${n_{e}}$, and ![]() ${T_{e}}$) appear similar in shape to the PSD of the GPI data, except that for high frequencies,
${T_{e}}$) appear similar in shape to the PSD of the GPI data, except that for high frequencies, ![]() $f \gtrsim 0.2\ \mathrm {MHz}$, a ‘ringing’ effect can be observed. This is due to internal data processing of the MLP, which smoothes data with a 12-point uniform filter as discussed previously (Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018b). Fitting (2.5) on the data yields
$f \gtrsim 0.2\ \mathrm {MHz}$, a ‘ringing’ effect can be observed. This is due to internal data processing of the MLP, which smoothes data with a 12-point uniform filter as discussed previously (Kube et al. Reference Kube, Garcia, Theodorsen, Brunner, Kuang, LaBombard and Terry2018b). Fitting (2.5) on the data yields ![]() ${\tau _{d}} = 10\ \mathrm {\mu } \mathrm {s}$ and
${\tau _{d}} = 10\ \mathrm {\mu } \mathrm {s}$ and ![]() $\lambda = 0.04$. The red and black lines in the right-hand panel show (2.5) and (2.4), respectively, with these parameters. Although (2.5) describes the Lorentzian-like decay of the experimental data as well as the ‘ringing’ effect at high frequencies, it underestimates the low-frequency part of the spectrum,
$\lambda = 0.04$. The red and black lines in the right-hand panel show (2.5) and (2.4), respectively, with these parameters. Although (2.5) describes the Lorentzian-like decay of the experimental data as well as the ‘ringing’ effect at high frequencies, it underestimates the low-frequency part of the spectrum, ![]() $f \lesssim 10^{-2}\ \mathrm {MHz}$. This is addressed by the deconvolution procedure.
$f \lesssim 10^{-2}\ \mathrm {MHz}$. This is addressed by the deconvolution procedure.
Summarizing the parameters found by fitting the GPI and MLP data, we find ![]() ${\tau _{d}} = 20\ \mathrm {\mu } \mathrm {s}$ and
${\tau _{d}} = 20\ \mathrm {\mu } \mathrm {s}$ and ![]() $\lambda = 1/10$ for GPI data and
$\lambda = 1/10$ for GPI data and ![]() ${\tau _{d}} = 10\ \mathrm {\mu } \mathrm {s}$ and
${\tau _{d}} = 10\ \mathrm {\mu } \mathrm {s}$ and ![]() $\lambda = 1/25$ for MLP data. In other words, the MLP observes shorter pulses that are more asymmetric than the GPI. As MLP and GPI measure different quantities, such differences might be expected. Other effects, rooted in the specific setup of each diagnostic may also contribute to differences in estimated pulse parameters. GPI measures light emissions from a finite volume (that is at least the 4 mm diameter spot size times the toroidal extent of the gas cloud) and pulses in the signal are due to radially and poloidally propagating blob structures. Therefore, it can be expected that the registered pulses in the signal appear more smeared out compared with those from the Langmuir probes, which measure plasma parameters at the probe tips. Such ‘pulse smearing’ is less of an issue for the MLP system owing to the small tip size.
$\lambda = 1/25$ for MLP data. In other words, the MLP observes shorter pulses that are more asymmetric than the GPI. As MLP and GPI measure different quantities, such differences might be expected. Other effects, rooted in the specific setup of each diagnostic may also contribute to differences in estimated pulse parameters. GPI measures light emissions from a finite volume (that is at least the 4 mm diameter spot size times the toroidal extent of the gas cloud) and pulses in the signal are due to radially and poloidally propagating blob structures. Therefore, it can be expected that the registered pulses in the signal appear more smeared out compared with those from the Langmuir probes, which measure plasma parameters at the probe tips. Such ‘pulse smearing’ is less of an issue for the MLP system owing to the small tip size.
Figures 9 and 10 show the results of the deconvolution procedure, starting with the PDF of the waiting times. The brown triangles give the estimated waiting times of the synthetically generated signal, whereas the black dotted line indicates an exponentialdecay. The GPI waiting time distribution conforms very well to the exponential decay of the synthetic time series for the entire distribution. The MLP waiting time distributions decay exponentially over at least two decades in probability. All waiting time distributions have lower probability of small waiting times (![]() ${\tau _{w}} / {\langle {\tau _{w}} \rangle } \lesssim 0.8$) compared with an exponential distribution, an artifact of the non-zero
${\tau _{w}} / {\langle {\tau _{w}} \rangle } \lesssim 0.8$) compared with an exponential distribution, an artifact of the non-zero ![]() ${\tau _{d}}$ and the peak-finding algorithm. This is also true for the synthetic time series.
${\tau _{d}}$ and the peak-finding algorithm. This is also true for the synthetic time series.

Figure 9. PDFs of waiting times obtained from deconvolving the GPI and MLP time series. The synthetically generated time series is indicated by ![]() $\varPsi$. The black dotted line indicates exponential decay.
$\varPsi$. The black dotted line indicates exponential decay.

Figure 10. PDFs of the pulse amplitudes obtained from deconvolving the GPI and MLP time series. The synthetically generated time series is indicated by ![]() $\varPsi$.
$\varPsi$.
Figure 10 shows the PDF of the pulse amplitudes obtained by applying the deconvolution procedure. The pulse amplitudes are approximately exponentially distributed for all analysed signals. The ![]() ${n_{e}}$ data and the synthetic process
${n_{e}}$ data and the synthetic process ![]() $\varPsi$ data both appear sub-exponential. On the other hand, the distribution of pulse amplitudes with both GPI data time series appears to be identical to the distribution reconstructed from the
$\varPsi$ data both appear sub-exponential. On the other hand, the distribution of pulse amplitudes with both GPI data time series appears to be identical to the distribution reconstructed from the ![]() ${I_{s}}$ and
${I_{s}}$ and ![]() ${T_{e}}$ data. For small and large amplitudes, the plotted PDFs show deviations from an exponential function. The deviation for large amplitudes is due to the finite size of the data time series. Deviations for small amplitudes are also observed in other measurement data (Theodorsen et al. Reference Theodorsen, Garcia, Kube, LaBombard and Terry2018).
${T_{e}}$ data. For small and large amplitudes, the plotted PDFs show deviations from an exponential function. The deviation for large amplitudes is due to the finite size of the data time series. Deviations for small amplitudes are also observed in other measurement data (Theodorsen et al. Reference Theodorsen, Garcia, Kube, LaBombard and Terry2018).
Together, these results indicate that the waiting times derived from the GPI and MLP data follow the same distribution and are consistent with exponentially distributed and independent waiting times. This further justifies using the stochastic model framework. The estimated average waiting times are presented in table 2, and give ![]() $\gamma$-values consistent with those obtained from fits to the histograms of the time series.
$\gamma$-values consistent with those obtained from fits to the histograms of the time series.
Table 2. Process and pulse parameters estimated using MLP and GPI data sampled in discharge 3.

The discrepancy between the low-frequency prediction of (2.4) and the PSD of the MLP data is resolved by the deconvolution procedure. In figure 11, the PSDs of the MLP data time series are presented together with the PSDs of the reconstructed time series and the analytic prediction. Note that the reconstructed time series uses the estimated ![]() ${\tau _{d}}$ and
${\tau _{d}}$ and ![]() $\gamma$ as input parameters. We also note that the experimental data has been normalized to their zero moving mean and unity moving root mean square, following (2.3). The length of the used filter is chosen as to remove low-frequency oscillations, but the quality is judged by eye. Thus, the low-frequency part of the spectrum may contain artifacts that are not captured by the stochastic model. The reconstructed time series give the same behaviour for low frequencies as the MLP data, showing that this discrepancy is explainable by the synthetic time series and is not a failure of the model.
$\gamma$ as input parameters. We also note that the experimental data has been normalized to their zero moving mean and unity moving root mean square, following (2.3). The length of the used filter is chosen as to remove low-frequency oscillations, but the quality is judged by eye. Thus, the low-frequency part of the spectrum may contain artifacts that are not captured by the stochastic model. The reconstructed time series give the same behaviour for low frequencies as the MLP data, showing that this discrepancy is explainable by the synthetic time series and is not a failure of the model.

Figure 11. Full line: PSDs of MLP time series. Dotted line: Reconstructed time series from the RL deconvolution. The black dashed line gives the PSD predicted by (2.4) for the two-sided exponential pulse.
Table 2 summarizes the parameter estimation. The first two rows list the parameters estimated using the methods described previously. The parameters listed in the bottom two rows provide consistency checks for the RL deconvolution. For the ![]() ${I_{s}}$ and
${I_{s}}$ and ![]() ${T_{e}}$ data, we find
${T_{e}}$ data, we find ![]() $\gamma \approx 1$. This describes a strongly intermittent time series with significant quiet time in between pulses. For the
$\gamma \approx 1$. This describes a strongly intermittent time series with significant quiet time in between pulses. For the ![]() ${n_{e}}$ time series we find
${n_{e}}$ time series we find ![]() $\gamma \approx 3.2$, comparable with the estimates for the GPI data. The average waiting time between pulses is
$\gamma \approx 3.2$, comparable with the estimates for the GPI data. The average waiting time between pulses is ![]() ${\langle {\tau _{w}} \rangle } \approx 8\ {\mathrm {\mu } \mathrm {s}}$. The best estimate for
${\langle {\tau _{w}} \rangle } \approx 8\ {\mathrm {\mu } \mathrm {s}}$. The best estimate for ![]() ${\langle {\tau _{w}} \rangle }$ from the
${\langle {\tau _{w}} \rangle }$ from the ![]() ${n_{e}}$ time series is given by
${n_{e}}$ time series is given by ![]() ${\langle {\tau _{w}} \rangle } \approx 3.3\ {\mathrm {\mu } \mathrm {s}}$, estimates from the GPI data are larger by a factor of two or three, depending on the radial position of the view. The pulse duration time for the MLP data is
${\langle {\tau _{w}} \rangle } \approx 3.3\ {\mathrm {\mu } \mathrm {s}}$, estimates from the GPI data are larger by a factor of two or three, depending on the radial position of the view. The pulse duration time for the MLP data is ![]() ${\tau _{d}} \approx 10\ {\mathrm {\mu } \mathrm {s}}$, smaller by a factor of two than for the GPI data, probably for the reasons discussed previously. The difference in average waiting time between
${\tau _{d}} \approx 10\ {\mathrm {\mu } \mathrm {s}}$, smaller by a factor of two than for the GPI data, probably for the reasons discussed previously. The difference in average waiting time between ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ suggests an abundance of blob structures with no or only small temperature variations.
${T_{e}}$ suggests an abundance of blob structures with no or only small temperature variations.
The bottom row lists the intermittency parameter calculated using the estimated pulse duration time and average waiting time, ![]() $\gamma = {\tau _{d}} / {\langle {\tau _{w}} \rangle }$. The deconvolution algorithm uses
$\gamma = {\tau _{d}} / {\langle {\tau _{w}} \rangle }$. The deconvolution algorithm uses ![]() ${\tau _{d}}$ from the power spectrum as an input parameter and
${\tau _{d}}$ from the power spectrum as an input parameter and ![]() $\gamma$ from the PDF fit as a constraint. Therefore, the fact that
$\gamma$ from the PDF fit as a constraint. Therefore, the fact that ![]() ${\tau _{d}} / {\langle {\tau _{w}} \rangle }$ is comparable with
${\tau _{d}} / {\langle {\tau _{w}} \rangle }$ is comparable with ![]() $\gamma$ estimated from the PDF fit is a confirming consistency check.
$\gamma$ estimated from the PDF fit is a confirming consistency check.
4. Conclusions and summary
Fluctuations of the SOL plasma have been studied for a series of ohmically heated discharges in Alcator C-Mod. It is found that the radial variations of the lowest-order statistical moments, calculated from MLP and GPI measurements, are quantitatively similar. Time-series data from both MLP and GPI diagnostics, feature intermittent, large-amplitude bursts. As shown in numerous previous publications, the time series are well described as a superposition of uncorrelated pulses with a two-sided exponential pulse shape and a pulse amplitude that closely follows an exponential distribution. In this contribution we demonstrate that the quantities that describe the various parameters of the stochastic process agree across MLP and GPI diagnostics. In particular, the same statistical properties apply to the ion saturation current, electron density and temperature and the line emission intensity.
Radial profiles of the relative fluctuation level, skewness and excess kurtosis, as estimated from both MLP and GPI data, are qualitatively similar and are monotonically increasing with distance from the LCFS. This holds regardless of using ![]() ${I_{s}}$,
${I_{s}}$, ![]() ${n_{e}}$ or
${n_{e}}$ or ![]() ${T_{e}}$ from the MLP. For the GPI data the time series feature an intermittency parameter
${T_{e}}$ from the MLP. For the GPI data the time series feature an intermittency parameter ![]() $\gamma \approx 2\text {--}3$, when estimated from a fit on the PDF. Estimating the intermittency parameter by a fit on the PDF of the different MLP data time series yields
$\gamma \approx 2\text {--}3$, when estimated from a fit on the PDF. Estimating the intermittency parameter by a fit on the PDF of the different MLP data time series yields ![]() $\gamma \approx 3$ for the
$\gamma \approx 3$ for the ![]() ${n_{e}}$ data and
${n_{e}}$ data and ![]() $\gamma \approx 1$ for both the
$\gamma \approx 1$ for both the ![]() ${I_{s}}$ and
${I_{s}}$ and ![]() ${T_{e}}$ data. Pulse duration times, estimated from fits on the time series frequency PSD, are
${T_{e}}$ data. Pulse duration times, estimated from fits on the time series frequency PSD, are ![]() ${\tau _{d}} \approx 10\ {\mathrm {\mu } \mathrm {s}}$ for all MLP data time series whereas we find
${\tau _{d}} \approx 10\ {\mathrm {\mu } \mathrm {s}}$ for all MLP data time series whereas we find ![]() ${\tau _{d}} \approx 20\ {\mathrm {\mu } \mathrm {s}}$ for the GPI data time series. This deviation by a factor of two is likely due to the relatively large in-focus spot size of the individual GPI views. Reconstructing the distributions of waiting times between consecutive pulses from a RL deconvolution, yields average waiting times between pulses of
${\tau _{d}} \approx 20\ {\mathrm {\mu } \mathrm {s}}$ for the GPI data time series. This deviation by a factor of two is likely due to the relatively large in-focus spot size of the individual GPI views. Reconstructing the distributions of waiting times between consecutive pulses from a RL deconvolution, yields average waiting times between pulses of ![]() ${\langle {\tau _{w}} \rangle } \approx (3,7,9)\ {\mathrm {\mu } \mathrm {s}}$ for the
${\langle {\tau _{w}} \rangle } \approx (3,7,9)\ {\mathrm {\mu } \mathrm {s}}$ for the ![]() $({n_{e}}, {T_{e}}, {I_{s}})$ data. Using GPI data time series, we find
$({n_{e}}, {T_{e}}, {I_{s}})$ data. Using GPI data time series, we find ![]() ${\langle {\tau _{w}} \rangle } \approx 5$ and
${\langle {\tau _{w}} \rangle } \approx 5$ and ![]() $10\ {\mathrm {\mu } \mathrm {s}}$ for the views at
$10\ {\mathrm {\mu } \mathrm {s}}$ for the views at ![]() $R=90.7$ and
$R=90.7$ and ![]() $91.0\ \mathrm {cm}$, respectively. We note that the GPI view at
$91.0\ \mathrm {cm}$, respectively. We note that the GPI view at ![]() $R=91.0\ \mathrm {cm}$ is close to the limiter shadow. Finally, estimating the intermittency parameter as
$R=91.0\ \mathrm {cm}$ is close to the limiter shadow. Finally, estimating the intermittency parameter as ![]() ${\tau _{d}} / {\langle {\tau _{w}} \rangle }$ from the deconvolution of the time series gives almost the same values as estimating
${\tau _{d}} / {\langle {\tau _{w}} \rangle }$ from the deconvolution of the time series gives almost the same values as estimating ![]() $\gamma$ by a fit on the PDF. These findings show that the model parameters of the stochastic model,
$\gamma$ by a fit on the PDF. These findings show that the model parameters of the stochastic model, ![]() $\gamma$,
$\gamma$, ![]() ${\tau _{d}}$ and
${\tau _{d}}$ and ![]() ${\langle {\tau _{w}} \rangle }$, are indeed a good parameterization of the plasma fluctuations, independent of the diagnostic used to measure them. Reconstructing the arrival times and amplitude of the individual pulses using RL deconvolution is an invaluable tool for obtaining the distribution of waiting times between consecutive pulses.
${\langle {\tau _{w}} \rangle }$, are indeed a good parameterization of the plasma fluctuations, independent of the diagnostic used to measure them. Reconstructing the arrival times and amplitude of the individual pulses using RL deconvolution is an invaluable tool for obtaining the distribution of waiting times between consecutive pulses.
Our analysis also suggests that calculating a synthetic line emission signal using the instantaneous plasma parameters reported by the MLP results in a signal with different fluctuation statistics than the time series actually measured by the GPI. The synthetic time-series data present intermittent pulses, but with a different shape than observed by the GPI. The PDF of these signals furthermore are close to a normal distribution, with low moments of skewness, excess kurtosis and no elevated tails. It is plausible that ionization, where hot plasma filaments locally decrease the puffed gas density, is the main cause of this phenomenon and therefore should be accounted for in such an attempt to reproduce the emission from measurements of ![]() ${n_{e}}$ and
${n_{e}}$ and ![]() ${T_{e}}$ (Thrysøe et al. Reference Thrysøe, Tophøj, Naulin, Rasmussen, Madsen and Nielsen2016; Wersal & Ricci Reference Wersal and Ricci2017).
${T_{e}}$ (Thrysøe et al. Reference Thrysøe, Tophøj, Naulin, Rasmussen, Madsen and Nielsen2016; Wersal & Ricci Reference Wersal and Ricci2017).
Having established ![]() $\gamma$,
$\gamma$, ![]() ${\tau _{d}}$ and
${\tau _{d}}$ and ![]() ${\langle {\tau _{w}} \rangle }$ as consistent estimators for fluctuations in the SOL, future work will focus on describing their variations with plasma parameters.
${\langle {\tau _{w}} \rangle }$ as consistent estimators for fluctuations in the SOL, future work will focus on describing their variations with plasma parameters.
Acknowledgements
This work was supported with financial subvention from the Research Council of Norway under Grant No. 240510/F20 and the from the US DoE under Cooperative Agreement No. DE-FC02-99ER54512 40 using the Alcator C-Mod tokamak, a DoE Office of Science user facility. This work was supported by the UiT Aurora Centre Program, UiT The Arctic University of Norway (2020). RK, OEG and AT acknowledge the generous hospitality of the MIT Plasma Science and Fusion Center during a research stay where part of this work was performed. JLT acknowledges the generous hospitality of UiT The Arctic University of Norway and its scientific staff during his stay there.
Editor Troy Carter thanks the referees for their advice in evaluating this article.
Appendix A. Local and global fluctuations
The emission intensity, measured by GPI, is often parameterized as
where ![]() $n_0$ is a constant neutral background density. Thus, the differential of
$n_0$ is a constant neutral background density. Thus, the differential of ![]() $I$ can be written as
$I$ can be written as
where we use the notation ![]() $\partial \ln f(x) / \partial \ln x = ( x/f(x) ) \partial f(x) / \partial x$. Assuming small fluctuation amplitudes, the differential of a function
$\partial \ln f(x) / \partial \ln x = ( x/f(x) ) \partial f(x) / \partial x$. Assuming small fluctuation amplitudes, the differential of a function ![]() $u$ can be approximated as
$u$ can be approximated as
Here, ![]() $\triangle u$ is a small, but non-infinitesimal change in
$\triangle u$ is a small, but non-infinitesimal change in ![]() $u$ and
$u$ and ![]() ${\langle u \rangle }$ denotes an average. That is, the relative, infinitesimal change in a function
${\langle u \rangle }$ denotes an average. That is, the relative, infinitesimal change in a function ![]() $u$ is approximately the deviation of
$u$ is approximately the deviation of ![]() $u$ to an average
$u$ to an average ![]() ${\langle u \rangle }$ relative to this average. This approximation gives the local density and temperature exponents
${\langle u \rangle }$ relative to this average. This approximation gives the local density and temperature exponents ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$:
$\beta$:
where ![]() $\alpha = \partial \ln f / \partial \ln {n_{e}}$ and
$\alpha = \partial \ln f / \partial \ln {n_{e}}$ and ![]() $\beta = \partial \ln f / \partial \ln {T_{e}}$ at a given (fixed)
$\beta = \partial \ln f / \partial \ln {T_{e}}$ at a given (fixed) ![]() ${\langle {n_{e}} \rangle }$ and
${\langle {n_{e}} \rangle }$ and ![]() ${\langle {T_{e}} \rangle }$.
${\langle {T_{e}} \rangle }$.
For large deviations relative to the mean values, this local approximation breaks down for two reasons. First, the infinitesimal change ![]() $\text {d} u$ can no longer be approximated as a variation relative to a mean value. Second, the partial derivatives in (A 2), which are evaluated at a fixed point, are not necessarily constant when using non-infinitesimal values for
$\text {d} u$ can no longer be approximated as a variation relative to a mean value. Second, the partial derivatives in (A 2), which are evaluated at a fixed point, are not necessarily constant when using non-infinitesimal values for ![]() $\mathrm {d} {n_{e}}$ or
$\mathrm {d} {n_{e}}$ or ![]() $\mathrm {d} {T_{e}}$. The local exponents are therefore not constant, and the full, global equation (A 1) must be used.
$\mathrm {d} {T_{e}}$. The local exponents are therefore not constant, and the full, global equation (A 1) must be used.