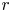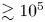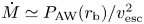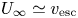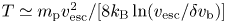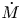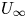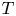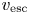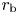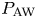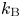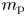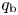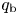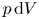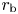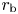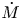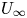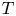1. Introduction
Pioneering works by Parker (Reference Parker1958, Reference Parker1965), Hartle & Sturrock (Reference Hartle and Sturrock1968), and Durney (Reference Durney1972) modelled the solar wind as a steady-state, spherical outflow powered by the outward conduction of heat from the base of the corona. These models succeeded in producing a supersonic wind, but were unable to explain the large outflow velocities measured in fast-solar-wind streams near Earth. They also had little predictive power for the mass outflow rate from the Sun, ![]() $\dot {M}$, because they specified the temperature of the coronal base as a boundary condition, and
$\dot {M}$, because they specified the temperature of the coronal base as a boundary condition, and ![]() $\dot {M}$ is highly sensitive to the coronal temperature (Hansteen & Leer Reference Hansteen and Leer1995).
$\dot {M}$ is highly sensitive to the coronal temperature (Hansteen & Leer Reference Hansteen and Leer1995).
A possible solution to these problems was proposed almost as soon as the difficulties became apparent, namely that the solar wind is powered by an Alfvén-wave (AW) energy flux (Parker Reference Parker1965, p. 686; Hollweg Reference Hollweg1973, Reference Hollweg1978). This idea received strong support from the discovery of large-amplitude AWs in the interplanetary medium that propagate away from the Sun in the local plasma frame (Belcher & Davis Reference Belcher and Davis1971) as well as the remote observation of AW-like motions in the low solar atmosphere carrying an energy flux sufficient to power the solar wind (De Pontieu et al. Reference De Pontieu, McIntosh, Carlsson, Hansteen, Tarbell, Schrijver, Title, Shine, Tsuneta and Katsukawa2007). A leading paradigm for how AWs energise the solar wind is based on reflection-driven AW turbulence. As AWs propagate away from the Sun, they undergo partial reflection because of the radial variation in the Alfvén speed (Heinemann & Olbert Reference Heinemann and Olbert1980; Velli Reference Velli1993). Counter-propagating AWs then interact nonlinearly (Iroshnikov Reference Iroshnikov1963; Kraichnan Reference Kraichnan1965), causing wave energy to cascade from large wavelengths to small wavelengths and dissipate, thereby heating the ambient plasma (Velli, Grappin & Mangeney Reference Velli, Grappin and Mangeney1989; Matthaeus et al. Reference Matthaeus, Zank, Oughton, Mullan and Dmitruk1999; Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005; Verdini & Velli Reference Verdini and Velli2007; Perez & Chandran Reference Perez and Chandran2013; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016, Reference van Ballegooijen and Asgari-Targhi2017). The presence of turbulence in the interplanetary medium is confirmed by spacecraft measurements (Coleman Reference Coleman1968; Matthaeus & Goldstein Reference Matthaeus and Goldstein1982; Tu & Marsch Reference Tu and Marsch1995; Smith et al. Reference Smith, Matthaeus, Zank, Ness, Oughton and Richardson2001; Bruno & Carbone Reference Bruno and Carbone2005; Horbury, Forman & Oughton Reference Horbury, Forman and Oughton2008; Wicks et al. Reference Wicks, Horbury, Chen and Schekochihin2010; Chen et al. Reference Chen, Bale, Bonnell, Borovikov, Bowen, Burgess, Case, Chandran, de Wit and Goetz2020), and numerical solar-wind models based on reflection-driven AW turbulence have proven successful at explaining a number of observations of the solar wind and corona (Cranmer, van Ballegooijen & Edgar Reference Cranmer, van Ballegooijen and Edgar2007; Verdini et al. Reference Verdini, Velli, Matthaeus, Oughton and Dmitruk2010; Chandran et al. Reference Chandran, Dennis, Quataert and Bale2011; van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester, Tóth and Gombosi2014; Usmanov, Goldstein & Matthaeus Reference Usmanov, Goldstein and Matthaeus2014). Three-dimensional compressible magnetohydrodynamic (MHD) simulations have also shown that the solar wind can be self-consistently generated by an AW energy flux (Shoda et al. Reference Shoda, Suzuki, Asgari-Targhi and Yokoyama2019).
Although the aforementioned numerical models reproduce many of the observed properties of the solar wind (see also Riley et al. Reference Riley, Lionello, Linker, Mikic, Luhmann and Wijaya2011; Gressl et al. Reference Gressl, Veronig, Temmer, Odstrčil, Linker, Mikić and Riley2014), analytic formulae that determine ![]() $\dot {M}$ and the outflow speed far from the Sun (
$\dot {M}$ and the outflow speed far from the Sun (![]() $U_\infty$) remain elusive. A number of studies have obtained a single equation that constrains the two unknowns
$U_\infty$) remain elusive. A number of studies have obtained a single equation that constrains the two unknowns ![]() $\dot {M}$ and
$\dot {M}$ and ![]() $U_{\infty }$. For example, Sandbaek, Leer & Hansteen (Reference Sandbaek, Leer and Hansteen1994) pointed out that if the energy flux far from the Sun is mostly in the form of bulk-flow kinetic energy, and if the energy flux at the coronal base is dominated by the flux of gravitational potential energy, heat, and some additional form of mechanical energy (from, e.g. AWs), then energy conservation implies that
$U_{\infty }$. For example, Sandbaek, Leer & Hansteen (Reference Sandbaek, Leer and Hansteen1994) pointed out that if the energy flux far from the Sun is mostly in the form of bulk-flow kinetic energy, and if the energy flux at the coronal base is dominated by the flux of gravitational potential energy, heat, and some additional form of mechanical energy (from, e.g. AWs), then energy conservation implies that
 \begin{equation} \dot{M} = \frac{\dot{E}_\textrm{m0} + \dot{E}_{q0}}{\frac{1}{2}(v_\textrm{esc}^2 + U_\infty^2)}, \end{equation}
\begin{equation} \dot{M} = \frac{\dot{E}_\textrm{m0} + \dot{E}_{q0}}{\frac{1}{2}(v_\textrm{esc}^2 + U_\infty^2)}, \end{equation}
where ![]() $\dot {E}_\textrm {m0}$ is the mechanical-energy input into the solar wind at the corona base,
$\dot {E}_\textrm {m0}$ is the mechanical-energy input into the solar wind at the corona base, ![]() $\dot {E}_{q0}$ is the energy input at the coronal base from thermal conduction (which is negative in models that include the lower solar atmosphere),
$\dot {E}_{q0}$ is the energy input at the coronal base from thermal conduction (which is negative in models that include the lower solar atmosphere),
 \begin{equation} v_\textrm{esc} = \left(\frac{2 G M_{{\odot}}}{R_{{\odot}}}\right)^{1/2} = 617.7 \mbox{ km} \mbox{ s}^{{-}1} \end{equation}
\begin{equation} v_\textrm{esc} = \left(\frac{2 G M_{{\odot}}}{R_{{\odot}}}\right)^{1/2} = 617.7 \mbox{ km} \mbox{ s}^{{-}1} \end{equation}
is the escape velocity of the Sun, ![]() $G$ is the gravitational constant,
$G$ is the gravitational constant, ![]() $M_\odot$ is the solar mass, and
$M_\odot$ is the solar mass, and ![]() $R_{\odot }$ is the solar radius. Schwadron & McComas (Reference Schwadron and McComas2003) derived a variant of (1.1) that explicitly relates
$R_{\odot }$ is the solar radius. Schwadron & McComas (Reference Schwadron and McComas2003) derived a variant of (1.1) that explicitly relates ![]() $\dot {E}_{q0}$ to the altitude of the coronal-temperature maximum. Hansteen & Leer (Reference Hansteen and Leer1995) and Hansteen, Leer & Holzer (Reference Hansteen, Leer and Holzer1997) showed that
$\dot {E}_{q0}$ to the altitude of the coronal-temperature maximum. Hansteen & Leer (Reference Hansteen and Leer1995) and Hansteen, Leer & Holzer (Reference Hansteen, Leer and Holzer1997) showed that ![]() $\dot {E}_{q0} \ll \dot {E}_\textrm {m0}$, and Hansteen & Velli (Reference Hansteen and Velli2012) made use of this finding to further refine (1.1), obtaining
$\dot {E}_{q0} \ll \dot {E}_\textrm {m0}$, and Hansteen & Velli (Reference Hansteen and Velli2012) made use of this finding to further refine (1.1), obtaining
 \begin{equation} \dot{M} = \frac{\dot{E}_\textrm{m0}}{\frac{1}{2}(v_\textrm{esc}^2 + U_\infty^2)}. \end{equation}
\begin{equation} \dot{M} = \frac{\dot{E}_\textrm{m0}}{\frac{1}{2}(v_\textrm{esc}^2 + U_\infty^2)}. \end{equation}
Another important result was obtained by Leer & Holzer (Reference Leer and Holzer1980), who found that heating inside the sonic critical point enhances ![]() $\dot {M}$ but has little effect on
$\dot {M}$ but has little effect on ![]() $U_{\infty }$, whereas heating beyond the sonic critical point increases
$U_{\infty }$, whereas heating beyond the sonic critical point increases ![]() $U_{\infty }$ but has little effect on
$U_{\infty }$ but has little effect on ![]() $\dot {M}$.
$\dot {M}$.
The main goal of the present paper is to obtain approximate analytic solutions for ![]() $\dot {M}$,
$\dot {M}$, ![]() $U_{\infty }$, the temperature of the corona, the heat flux from the coronal base into the lower solar atmosphere, and the plasma density at the coronal base under the assumption that AW turbulence is the primary energisation mechanism of the solar wind. Section 2 takes a first step towards this goal by presenting a simplified approximate calculation of
$U_{\infty }$, the temperature of the corona, the heat flux from the coronal base into the lower solar atmosphere, and the plasma density at the coronal base under the assumption that AW turbulence is the primary energisation mechanism of the solar wind. Section 2 takes a first step towards this goal by presenting a simplified approximate calculation of ![]() $\dot {M}$,
$\dot {M}$, ![]() $U_{\infty }$, and the coronal temperature. Section 3 develops a more detailed solar-wind model that accounts for physical processes neglected in § 2. Approximate analytic solutions to the equations of this model are presented in § 3, and numerical solutions are presented in § 4. Section 5 discusses and summarises the main results of the paper.
$U_{\infty }$, and the coronal temperature. Section 3 develops a more detailed solar-wind model that accounts for physical processes neglected in § 2. Approximate analytic solutions to the equations of this model are presented in § 3, and numerical solutions are presented in § 4. Section 5 discusses and summarises the main results of the paper.
2. Heuristic calculation of  $\dot {M}$,
$\dot {M}$,  $U_{\infty }$, and the coronal temperature in AW-driven winds with minimal conductive losses
$U_{\infty }$, and the coronal temperature in AW-driven winds with minimal conductive losses
Approximate expressions for ![]() $\dot {M}$,
$\dot {M}$, ![]() $U_\infty$, and the coronal temperature can be quickly obtained by modelling the solar wind as a spherically symmetric, steady-state outflow and assuming that: (1) AW turbulence is the dominant heating mechanism; (2) solar rotation can be neglected, so that the magnetic field
$U_\infty$, and the coronal temperature can be quickly obtained by modelling the solar wind as a spherically symmetric, steady-state outflow and assuming that: (1) AW turbulence is the dominant heating mechanism; (2) solar rotation can be neglected, so that the magnetic field ![]() $\boldsymbol {B}$ and flow velocity are aligned; (3)
$\boldsymbol {B}$ and flow velocity are aligned; (3) ![]() $\boldsymbol {B}\propto r^{-2}\boldsymbol {\hat {r}}$, where
$\boldsymbol {B}\propto r^{-2}\boldsymbol {\hat {r}}$, where ![]() $\boldsymbol {\hat {r}}$ is the radial unit vector (i.e. a split monopole, with
$\boldsymbol {\hat {r}}$ is the radial unit vector (i.e. a split monopole, with ![]() $B_r>0$ in one hemisphere and
$B_r>0$ in one hemisphere and ![]() $B_r<0$ in the other); (4) momentum deposition by AWs can be neglected between the coronal base and sonic critical point; and (5)
$B_r<0$ in the other); (4) momentum deposition by AWs can be neglected between the coronal base and sonic critical point; and (5) ![]() $p\,\textrm {d} V$ work is the dominant sink of internal energy in the sub-Alfvénic region of the solar wind, in which the solar-wind outflow velocity
$p\,\textrm {d} V$ work is the dominant sink of internal energy in the sub-Alfvénic region of the solar wind, in which the solar-wind outflow velocity ![]() $U$ is smaller than the Alfvén speed
$U$ is smaller than the Alfvén speed
where ![]() $\rho$ is the mass density. Assumptions (3)–(5) are relaxed in the next section.
$\rho$ is the mass density. Assumptions (3)–(5) are relaxed in the next section.
In steady state, given assumption (2) above, mass and flux conservation imply (see § 3.1) that
where
 \begin{equation} y_\textrm{b} \equiv \left[\frac{\rho_\textrm{b}}{\rho(r_\textrm{A})}\right]^{1/2}, \end{equation}
\begin{equation} y_\textrm{b} \equiv \left[\frac{\rho_\textrm{b}}{\rho(r_\textrm{A})}\right]^{1/2}, \end{equation}
![]() $\rho _\textrm {b} = \rho (r_\textrm {b})$,
$\rho _\textrm {b} = \rho (r_\textrm {b})$, ![]() $r_\textrm {b}$ is the radius of the coronal base, which in this section (but not the next) is simply set equal to
$r_\textrm {b}$ is the radius of the coronal base, which in this section (but not the next) is simply set equal to ![]() $R_{\odot }$,
$R_{\odot }$, ![]() $r_\textrm {A}$ is the Alfvén critical point at which
$r_\textrm {A}$ is the Alfvén critical point at which ![]() $U=v_\textrm {A}$,
$U=v_\textrm {A}$, ![]() $v_\textrm {Ab} = v_\textrm {A}(r_\textrm {b})$, and
$v_\textrm {Ab} = v_\textrm {A}(r_\textrm {b})$, and ![]() $U_\textrm {b} = U(r_\textrm {b})$. The mass outflow rate can thus be written in the form
$U_\textrm {b} = U(r_\textrm {b})$. The mass outflow rate can thus be written in the form
As shown in § 3.2, heating by reflection-driven AW turbulence causes the sub-Alfvénic part of the solar wind at ![]() $r< r_\textrm {A}$ to become quasi-isothermal, in the sense that
$r< r_\textrm {A}$ to become quasi-isothermal, in the sense that
where
is the square of the isothermal sound speed, ![]() $k_\textrm {B}$ is the Boltzmann constant,
$k_\textrm {B}$ is the Boltzmann constant, ![]() $T$ is the temperature, and
$T$ is the temperature, and ![]() $m_\textrm {p}$ is the proton mass. This argument is consistent with observations and models of the solar wind, which suggest that the temperature varies by a factor of only a few between
$m_\textrm {p}$ is the proton mass. This argument is consistent with observations and models of the solar wind, which suggest that the temperature varies by a factor of only a few between ![]() $r_\textrm {b}$ and
$r_\textrm {b}$ and ![]() $r_\textrm {A}$, whereas
$r_\textrm {A}$, whereas ![]() $\rho$ varies by a factor of approximately
$\rho$ varies by a factor of approximately ![]() $10^5$ (see, e.g. Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007). When the sub-Alfvénic solar wind is approximated as an isothermal plasma, the momentum equation at
$10^5$ (see, e.g. Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007). When the sub-Alfvénic solar wind is approximated as an isothermal plasma, the momentum equation at ![]() $r<r_\textrm {A}$ can be written in the form
$r<r_\textrm {A}$ can be written in the form
As ![]() $\dot {M} = 4{\rm \pi} r^2 U \rho$ is independent of
$\dot {M} = 4{\rm \pi} r^2 U \rho$ is independent of ![]() $r$,
$r$, ![]() $U^{-1} \,\textrm {d} U/\textrm {d} r = - \rho ^{-1} \,\textrm {d} \rho / \textrm {d} r - 2/r$. Upon substituting this relation into (2.7) and rearranging terms, one obtains
$U^{-1} \,\textrm {d} U/\textrm {d} r = - \rho ^{-1} \,\textrm {d} \rho / \textrm {d} r - 2/r$. Upon substituting this relation into (2.7) and rearranging terms, one obtains
In order for (2.8) to have a smooth transonic solution, the right-hand side of (2.8) must vanish at the radius ![]() $r_\textrm {c}$ at which
$r_\textrm {c}$ at which ![]() $U=c_\textrm {s}$, so that
$U=c_\textrm {s}$, so that ![]() $\textrm {d} \rho /\textrm {d} r$ remains finite. This leads to the two critical-point conditions
$\textrm {d} \rho /\textrm {d} r$ remains finite. This leads to the two critical-point conditions
where ![]() $U_\textrm {c} = U(r_\textrm {c})$. Integrating (2.7), one obtains the Bernoulli integral
$U_\textrm {c} = U(r_\textrm {c})$. Integrating (2.7), one obtains the Bernoulli integral
where the second equality in (2.10) results from evaluating the left-hand side of (2.10) at ![]() $r=r_\textrm {b}$ and dropping the
$r=r_\textrm {b}$ and dropping the ![]() $U_\textrm {b}^2/2$ term, which is
$U_\textrm {b}^2/2$ term, which is ![]() $\ll v_\textrm {esc}^2/2$. After evaluating the left-hand side of (2.10) at
$\ll v_\textrm {esc}^2/2$. After evaluating the left-hand side of (2.10) at ![]() $r=r_\textrm {c}$ and using (2.9) to rewrite
$r=r_\textrm {c}$ and using (2.9) to rewrite ![]() $U_\textrm {c}$ and
$U_\textrm {c}$ and ![]() $r_\textrm {c}$ in terms of
$r_\textrm {c}$ in terms of ![]() $c_\textrm {s}^2$, one obtains
$c_\textrm {s}^2$, one obtains
where ![]() $\rho _\textrm {c} = \rho (r_\textrm {c})$. Upon setting
$\rho _\textrm {c} = \rho (r_\textrm {c})$. Upon setting ![]() $\dot {M} = 4{\rm \pi} r_\textrm {c}^2 \rho _\textrm {c} U_\textrm {c}$ and using (2.9) and (2.11) to rewrite
$\dot {M} = 4{\rm \pi} r_\textrm {c}^2 \rho _\textrm {c} U_\textrm {c}$ and using (2.9) and (2.11) to rewrite ![]() $r_\textrm {c}$,
$r_\textrm {c}$, ![]() $\rho _\textrm {c}$, and
$\rho _\textrm {c}$, and ![]() $U_\textrm {c}$ in terms of
$U_\textrm {c}$ in terms of ![]() $c_\textrm {s}$, one obtains (Hansteen & Velli Reference Hansteen and Velli2012)
$c_\textrm {s}$, one obtains (Hansteen & Velli Reference Hansteen and Velli2012)
The exponential appearing on the right-hand side of (2.12) reflects the fact that, at ![]() $r< r_\textrm {c}$, the flow is subsonic and the density drops off approximately as in a static atmosphere (Hansteen & Velli Reference Hansteen and Velli2012). Equating the right-hand sides of (2.4) and (2.12), one finds that
$r< r_\textrm {c}$, the flow is subsonic and the density drops off approximately as in a static atmosphere (Hansteen & Velli Reference Hansteen and Velli2012). Equating the right-hand sides of (2.4) and (2.12), one finds that
where ![]() $c_1 \equiv e^{3/2} v_\textrm {esc}^4/(16 c_\textrm {s}^3 v_\textrm {Ab})$.
$c_1 \equiv e^{3/2} v_\textrm {esc}^4/(16 c_\textrm {s}^3 v_\textrm {Ab})$.
When radiative cooling and thermal conduction are neglected, the internal-energy equation becomes
where ![]() $Q$ is the turbulent heating rate, and
$Q$ is the turbulent heating rate, and ![]() $\gamma$ is the ratio of specific heats. In the quasi-isothermal approximation, the second term on the left-hand side of (2.14) can be neglected. Multiplying (2.14) by
$\gamma$ is the ratio of specific heats. In the quasi-isothermal approximation, the second term on the left-hand side of (2.14) can be neglected. Multiplying (2.14) by ![]() $4{\rm \pi} r^2$ and integrating over the quasi-isothermal sub-Alfvénic region, one obtains
$4{\rm \pi} r^2$ and integrating over the quasi-isothermal sub-Alfvénic region, one obtains
where the approximate equality assumes that the volume-integrated turbulent heating rate between ![]() $r_\textrm {b}$ and
$r_\textrm {b}$ and ![]() $r_\textrm {A}$ is comparable to
$r_\textrm {A}$ is comparable to ![]() $P_\textrm {AW}(r_\textrm {b})$, the power carried by outward-propagating AWs at the coronal base, consistent with direct numerical simulations (Perez et al. Reference Perez, Chandran, Klein and Martinovic2021). As
$P_\textrm {AW}(r_\textrm {b})$, the power carried by outward-propagating AWs at the coronal base, consistent with direct numerical simulations (Perez et al. Reference Perez, Chandran, Klein and Martinovic2021). As ![]() $\ln (\rho _\textrm {b}/\rho (r_\textrm {A})) = 2 \ln y_\textrm {b}$, (2.15) yields
$\ln (\rho _\textrm {b}/\rho (r_\textrm {A})) = 2 \ln y_\textrm {b}$, (2.15) yields
where the second relation in (2.16) follows from (2.13).
Equations (2.15) and (2.16) can be understood as follows. Within the quasi-isothermal sub-Alfvénic region, each time the density of a parcel of plasma decreases by a factor of ![]() $e$, its thermal energy must be replaced via heating to offset internal-energy losses from
$e$, its thermal energy must be replaced via heating to offset internal-energy losses from ![]() $p\,\textrm {d} V$ work. The quantity
$p\,\textrm {d} V$ work. The quantity ![]() $c_\textrm {s}^2 \ln (\rho _\textrm {b}/\rho (r_\textrm {A})) = 2 c_\textrm {s}^2 \ln y_\textrm {b} \simeq v_\textrm {esc}^2$ is thus the heating cost per unit mass for plasma to transit the sub-Alfvénic region. The reason that the product
$c_\textrm {s}^2 \ln (\rho _\textrm {b}/\rho (r_\textrm {A})) = 2 c_\textrm {s}^2 \ln y_\textrm {b} \simeq v_\textrm {esc}^2$ is thus the heating cost per unit mass for plasma to transit the sub-Alfvénic region. The reason that the product ![]() $c_\textrm {s}^2 \ln (\rho _\textrm {b}/\rho (r_\textrm {A}))$ is approximately constant is that increasing
$c_\textrm {s}^2 \ln (\rho _\textrm {b}/\rho (r_\textrm {A}))$ is approximately constant is that increasing ![]() $c_\textrm {s}^2$ leads to an exponential increase in
$c_\textrm {s}^2$ leads to an exponential increase in ![]() $\dot {M}$ and the solar-wind density and an exponential reduction of
$\dot {M}$ and the solar-wind density and an exponential reduction of ![]() $\rho _\textrm {b}/\rho (r_\textrm {A})$, leaving
$\rho _\textrm {b}/\rho (r_\textrm {A})$, leaving ![]() $c_\textrm {s}^2 \ln (\rho _\textrm {b}/\rho (r_\textrm {A}))$ approximately unchanged. Equations (2.15) and (2.16) state that
$c_\textrm {s}^2 \ln (\rho _\textrm {b}/\rho (r_\textrm {A}))$ approximately unchanged. Equations (2.15) and (2.16) state that ![]() $\dot {M}$ is the net heating power within the sub-Alfvénic region (which is taken to be
$\dot {M}$ is the net heating power within the sub-Alfvénic region (which is taken to be ![]() $\simeq P_\textrm {AW}(r_\textrm {b})$) divided by the heating cost per unit mass.
$\simeq P_\textrm {AW}(r_\textrm {b})$) divided by the heating cost per unit mass.
Assuming that the AW-energy flux and gravitational-potential-energy flux are the dominant mechanical-energy fluxes at the coronal base and that the kinetic-energy flux is the dominant mechanical-energy flux at large ![]() $r$, and equating the mechanical luminosities at
$r$, and equating the mechanical luminosities at ![]() $r=r_\textrm {b}$ and at large
$r=r_\textrm {b}$ and at large ![]() $r$, one obtains
$r$, one obtains
Substituting (2.16) into (2.17) yields
Reflection-driven AW turbulence thus changes the energy per unit mass from ![]() $\simeq - v_\textrm {esc}^2/2$ at the coronal base to
$\simeq - v_\textrm {esc}^2/2$ at the coronal base to ![]() $\simeq v_\textrm {esc}^2/2$ far from the Sun.
$\simeq v_\textrm {esc}^2/2$ far from the Sun.
In the absence of super-radial expansion, ![]() $P_\textrm {AW}(r_\textrm {b}) = 4 {\rm \pi}R_{\odot }^2 v_\textrm {Ab} \rho _\textrm {b} (\delta v_\textrm {b})^2$, where
$P_\textrm {AW}(r_\textrm {b}) = 4 {\rm \pi}R_{\odot }^2 v_\textrm {Ab} \rho _\textrm {b} (\delta v_\textrm {b})^2$, where ![]() $\delta v_\textrm {b}$ is the root-mean-square (r.m.s.) amplitude of the fluctuating velocity at the coronal base. This relation, in conjunction with (2.4) and (2.16), implies that
$\delta v_\textrm {b}$ is the root-mean-square (r.m.s.) amplitude of the fluctuating velocity at the coronal base. This relation, in conjunction with (2.4) and (2.16), implies that ![]() $y_\textrm {b} \simeq v_\textrm {esc}^2 / (\delta v_\textrm {b})^2$, which leads via (2.6) and (2.13) to the approximate value of the coronal temperature,
$y_\textrm {b} \simeq v_\textrm {esc}^2 / (\delta v_\textrm {b})^2$, which leads via (2.6) and (2.13) to the approximate value of the coronal temperature,
A number of factors can cause ![]() $\dot {M}$,
$\dot {M}$, ![]() $U_{\infty }$, and the coronal temperature to deviate from the estimates in (2.16) (2.18), and (2.19). For example, some of the AW power survives out to
$U_{\infty }$, and the coronal temperature to deviate from the estimates in (2.16) (2.18), and (2.19). For example, some of the AW power survives out to ![]() $r_\textrm {A}$, which reduces the total turbulent heating in the sub-Alfvénic region appearing on the right-hand side of (2.15), which, in turn, reduces
$r_\textrm {A}$, which reduces the total turbulent heating in the sub-Alfvénic region appearing on the right-hand side of (2.15), which, in turn, reduces ![]() $\dot {M}$. The heat that is conducted from the corona into the transition region adds a negative sink term to the right-hand sides of (2.14) and (2.15), which likewise acts to reduce
$\dot {M}$. The heat that is conducted from the corona into the transition region adds a negative sink term to the right-hand sides of (2.14) and (2.15), which likewise acts to reduce ![]() $\dot {M}$. On the other hand, the AW pressure force helps drive plasma away from the Sun at the critical point, which acts to increase
$\dot {M}$. On the other hand, the AW pressure force helps drive plasma away from the Sun at the critical point, which acts to increase ![]() $\dot {M}$. These effects, as well as super-radial expansion of the magnetic field, are included in the more detailed solar-wind model developed in the next section.
$\dot {M}$. These effects, as well as super-radial expansion of the magnetic field, are included in the more detailed solar-wind model developed in the next section.
3. Steady-state model of the transition region, corona, and solar wind
The lowest layer of the solar atmosphere is the chromosphere, which extends 2000–3000 km above the photosphere with a temperature ![]() $T$ ranging from several thousand
$T$ ranging from several thousand ![]() $K$ to around
$K$ to around ![]() $10^4$ K. Bounding the chromosphere from above is the transition region, a narrow layer approximately
$10^4$ K. Bounding the chromosphere from above is the transition region, a narrow layer approximately ![]() $100$ km thick, in which the density
$100$ km thick, in which the density ![]() $\rho$ drops (and
$\rho$ drops (and ![]() $T$ increases) by approximately two orders of magnitude. Above the transition region lies the corona, which extends out a few solar radii from the Sun and has a temperature of around
$T$ increases) by approximately two orders of magnitude. Above the transition region lies the corona, which extends out a few solar radii from the Sun and has a temperature of around ![]() $10^6$ K. The corona contains both closed magnetic loops, which connect back to the Sun at both ends, and open magnetic-field lines that connect the solar surface to the distant interplanetary medium. Regions of the corona permeated by open magnetic-field lines have lower densities than closed-field-line regions and are referred to as coronal holes. In the analysis to follow,
$10^6$ K. The corona contains both closed magnetic loops, which connect back to the Sun at both ends, and open magnetic-field lines that connect the solar surface to the distant interplanetary medium. Regions of the corona permeated by open magnetic-field lines have lower densities than closed-field-line regions and are referred to as coronal holes. In the analysis to follow, ![]() $r_\textrm {b}$ denotes the radius of the coronal base just above the transition region in Sun-centred spherical coordinates
$r_\textrm {b}$ denotes the radius of the coronal base just above the transition region in Sun-centred spherical coordinates ![]() $(r, \theta , \phi )$, which is taken to be
$(r, \theta , \phi )$, which is taken to be
The steady-state model developed in this section describes the outflowing plasma within an open magnetic flux tube from the transition region to beyond the Alfvén critical point ![]() $r_\textrm {A}$, at which the plasma outflow velocity
$r_\textrm {A}$, at which the plasma outflow velocity ![]() $U$ equals
$U$ equals ![]() $v_\textrm {A}$. Figure 1 provides a schematic overview of the model, which determines five unknowns – the density at the coronal base
$v_\textrm {A}$. Figure 1 provides a schematic overview of the model, which determines five unknowns – the density at the coronal base ![]() $\rho _\textrm {b}$, the temperature of the quasi-isothermal sub-Alfvénic region, the mass outflow rate
$\rho _\textrm {b}$, the temperature of the quasi-isothermal sub-Alfvénic region, the mass outflow rate ![]() $\dot {M}$, the asymptotic outflow velocity
$\dot {M}$, the asymptotic outflow velocity ![]() $U_\infty$, and the flux of heat from the coronal base into the transition region
$U_\infty$, and the flux of heat from the coronal base into the transition region ![]() $q_\textrm {b}$ – through the following five steps:
$q_\textrm {b}$ – through the following five steps:

Figure 1. Schematic overview of model.
(i) balancing turbulent heating at
 $r=r_\textrm {b}$ against radiative cooling at
$r=r_\textrm {b}$ against radiative cooling at  $r=r_\textrm {b}$;
$r=r_\textrm {b}$;(ii) balancing the total turbulent heating between
 $r_\textrm {b}$ and
$r_\textrm {b}$ and  $r_\textrm {A}$ against the two primary sinks of internal energy in this region,
$r_\textrm {A}$ against the two primary sinks of internal energy in this region,  $p\,\textrm {d} V$ work and the flux of heat into the transition region;
$p\,\textrm {d} V$ work and the flux of heat into the transition region;(iii) balancing, within the transition region, conductive heating against internal-energy losses from
 $p\,\textrm {d} V$ work, advection, and radiation;
$p\,\textrm {d} V$ work, advection, and radiation;(iv) equating the mass outflow rate at
 $r=r_\textrm {b}$ with the mass outflow rate at the wave-modified sonic critical point
$r=r_\textrm {b}$ with the mass outflow rate at the wave-modified sonic critical point  $r=r_\textrm {c}$; and
$r=r_\textrm {c}$; and(v) equating the wave-modified Bernoulli integral at
 $r=r_\textrm {b}$ and
$r=r_\textrm {b}$ and  $r=r_\textrm {c}$.
$r=r_\textrm {c}$.
These five steps are detailed in §§ 3.4–3.7. Section 3.1 reviews some identities that follow from the conservation of mass and magnetic flux. Sections 3.2 and 3.3 review previous results on reflection-driven AW turbulence in the solar wind and present the simplified model of reflection-driven AW turbulence that is used in this paper. A glossary is given in table 1.
Table 1. Glossary.

3.1. Flux and mass conservation
To simplify the analysis, solar rotation is neglected, and the magnetic field is taken to be radial, except in the corona, where open magnetic-field lines fan out to fill the space above closed magnetic loops at lower altitudes. Mathematically,
where ![]() $\eta (r)$ is the local super-radial expansion factor, which approaches 1 when
$\eta (r)$ is the local super-radial expansion factor, which approaches 1 when ![]() $r/R_{\odot } \gg 1$, and
$r/R_{\odot } \gg 1$, and ![]() $\bar {B}$ is the magnetic-field strength that would arise at the photosphere in the absence of super-radial expansion (i.e. if
$\bar {B}$ is the magnetic-field strength that would arise at the photosphere in the absence of super-radial expansion (i.e. if ![]() $\eta (r)$ were unity everywhere.) Given (3.2), the magnetic-field strength at the coronal base is
$\eta (r)$ were unity everywhere.) Given (3.2), the magnetic-field strength at the coronal base is
where here and in the following a ‘b’ subscript indicates that the subscripted quantity is evaluated at ![]() $r=r_\textrm {b}$, and
$r=r_\textrm {b}$, and
Because rotation is neglected, the steady-state solar-wind outflow velocity is aligned with the background magnetic field (Mestel Reference Mestel1961):
The density and velocity satisfy the steady-state continuity equation,
It follows from (3.5), (3.6), and ![]() ${\boldsymbol{\nabla}\,\boldsymbol{\cdot}}\, \boldsymbol {B}=0$ that
${\boldsymbol{\nabla}\,\boldsymbol{\cdot}}\, \boldsymbol {B}=0$ that ![]() $\boldsymbol {B} \cdot \boldsymbol {\nabla }( \rho U / B) = 0$, and, hence,
$\boldsymbol {B} \cdot \boldsymbol {\nabla }( \rho U / B) = 0$, and, hence,
Equation (3.7) is equivalent to
where
is the cross-sectional area of the flow, which satisfies ![]() $A(r) = \mbox {constant}/ B(r)$, as required by flux conservation. Equations (3.8) and (3.9) follow the convention of expressing the mass outflow rate as the total solar mass-loss rate that would arise if the local mass flux at some
$A(r) = \mbox {constant}/ B(r)$, as required by flux conservation. Equations (3.8) and (3.9) follow the convention of expressing the mass outflow rate as the total solar mass-loss rate that would arise if the local mass flux at some ![]() $r$ characterised the entire outflow at that
$r$ characterised the entire outflow at that ![]() $r$, even though the actual solar wind is comprised of different wind streams with different properties. All of the results of this paper can be applied to an individual flux tube accounting for some fraction
$r$, even though the actual solar wind is comprised of different wind streams with different properties. All of the results of this paper can be applied to an individual flux tube accounting for some fraction ![]() $\nu$ of the total flow area by multiplying the right-hand side of (3.9) by
$\nu$ of the total flow area by multiplying the right-hand side of (3.9) by ![]() $\nu$.
$\nu$.
It follows from (2.1) and (3.7) that ![]() $\rho ^{1/2} U/v_\textrm {A}$ is a constant. Because
$\rho ^{1/2} U/v_\textrm {A}$ is a constant. Because ![]() $U(r_\textrm {A}) = v_\textrm {A}(r_\textrm {A})$, this constant must be
$U(r_\textrm {A}) = v_\textrm {A}(r_\textrm {A})$, this constant must be ![]() $\rho _\textrm {A}^{1/2}$, where
$\rho _\textrm {A}^{1/2}$, where
Thus,
where
 \begin{equation} y \equiv \left(\frac{\rho}{\rho_\textrm{A}}\right)^{1/2}. \end{equation}
\begin{equation} y \equiv \left(\frac{\rho}{\rho_\textrm{A}}\right)^{1/2}. \end{equation}With the aid of (3.3), (3.4), (3.9) and (3.11), (3.8) can be rewritten as
Thus, ![]() $\dot {M}$ is determined uniquely by the value of
$\dot {M}$ is determined uniquely by the value of ![]() $\rho _\textrm {A}$ and the single-hemisphere open magnetic flux,
$\rho _\textrm {A}$ and the single-hemisphere open magnetic flux, ![]() $2 {\rm \pi}R_{\odot }^2 \bar {B}$.
$2 {\rm \pi}R_{\odot }^2 \bar {B}$.
3.2. Reflection-driven AW turbulence
Dmitruk et al. (Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002) (hereafter D02) developed an analytic model of reflection-driven AW turbulence in the solar corona valid in the limit of small ![]() $L_\perp$, where
$L_\perp$, where ![]() $L_\perp$ is the correlation length of the AW fluctuations measured in the plane perpendicular to the background magnetic field. Chandran & Hollweg (Reference Chandran and Hollweg2009) (hereafter CH09) generalised this model by accounting for the solar-wind outflow velocity. Section 3.2.1 summarises the main results of the CH09 model, and § 3.2.2 uses the CH09 model to show that heating by reflection-driven AW turbulence causes the sub-Alfvénic region of the solar wind (at
$L_\perp$ is the correlation length of the AW fluctuations measured in the plane perpendicular to the background magnetic field. Chandran & Hollweg (Reference Chandran and Hollweg2009) (hereafter CH09) generalised this model by accounting for the solar-wind outflow velocity. Section 3.2.1 summarises the main results of the CH09 model, and § 3.2.2 uses the CH09 model to show that heating by reflection-driven AW turbulence causes the sub-Alfvénic region of the solar wind (at ![]() $r<r_\textrm {A}$, where
$r<r_\textrm {A}$, where ![]() $U< v_\textrm {A}$) to become approximately isothermal. Section 3.2.3 presents a modified version of the CH09 model that is easier to work with analytically, which is used to incorporate AW turbulence into the solar-wind model developed in this section.
$U< v_\textrm {A}$) to become approximately isothermal. Section 3.2.3 presents a modified version of the CH09 model that is easier to work with analytically, which is used to incorporate AW turbulence into the solar-wind model developed in this section.
3.2.1. The Chandran & Hollweg (2009) model of reflection-driven AW turbulence
In classical mechanics, a simple harmonic oscillator with frequency ![]() $\omega$ and energy
$\omega$ and energy ![]() $E$ possesses an adiabatic invariant
$E$ possesses an adiabatic invariant ![]() $E/\omega$. If the parameters of the oscillator vary on a time scale
$E/\omega$. If the parameters of the oscillator vary on a time scale ![]() $t_0$ satisfying
$t_0$ satisfying ![]() $t_0 \gg \omega ^{-1}$ (e.g. if the length of a pendulum is slowly varied), then
$t_0 \gg \omega ^{-1}$ (e.g. if the length of a pendulum is slowly varied), then ![]() $E/\omega$ is almost exactly conserved. As
$E/\omega$ is almost exactly conserved. As ![]() $(\omega t_0)^{-1} \rightarrow 0$, changes in
$(\omega t_0)^{-1} \rightarrow 0$, changes in ![]() $E/\omega$ vanish faster than any power of
$E/\omega$ vanish faster than any power of ![]() $(\omega t_0)^{-1}$ (Landau & Lifshitz Reference Landau and Lifshitz1960).
$(\omega t_0)^{-1}$ (Landau & Lifshitz Reference Landau and Lifshitz1960).
An AW is like a space-filling collection of harmonic oscillators, and the wave action is analogous to the harmonic oscillator's adiabatic invariant. The wave action per unit volume per unit ![]() $\omega$ is
$\omega$ is ![]() ${\mathcal {E}}_\omega / \omega ^\prime$, where
${\mathcal {E}}_\omega / \omega ^\prime$, where ![]() $\omega$ is the AW frequency in an inertial frame centred on the Sun,
$\omega$ is the AW frequency in an inertial frame centred on the Sun, ![]() $\omega ^\prime$ is the AW frequency in the local plasma frame, and
$\omega ^\prime$ is the AW frequency in the local plasma frame, and ![]() ${\mathcal {E}}_\omega$ is the AW energy per unit volume per unit
${\mathcal {E}}_\omega$ is the AW energy per unit volume per unit ![]() $\omega$. In the Wentzel-Kramers-Brillouin (WKB) limit, in which the wave period is much shorter than the time scale on which the plasma parameters vary appreciably and the wave length is much shorter than the length scales over which the background plasma varies appreciably, the wave action satisfies the conservation law
$\omega$. In the Wentzel-Kramers-Brillouin (WKB) limit, in which the wave period is much shorter than the time scale on which the plasma parameters vary appreciably and the wave length is much shorter than the length scales over which the background plasma varies appreciably, the wave action satisfies the conservation law
where ![]() $\boldsymbol {c}$ is the group velocity of the waves (Bretherton & Garrett Reference Bretherton and Garrett1968; Dewar Reference Dewar1970). For outward-propagating AWs in the solar wind,
$\boldsymbol {c}$ is the group velocity of the waves (Bretherton & Garrett Reference Bretherton and Garrett1968; Dewar Reference Dewar1970). For outward-propagating AWs in the solar wind, ![]() $\omega = k_r(U+v_\textrm {A})$,
$\omega = k_r(U+v_\textrm {A})$, ![]() $\omega ^\prime = k_r v_\textrm {A}$, and
$\omega ^\prime = k_r v_\textrm {A}$, and ![]() $\boldsymbol {c} = (U+v_\textrm {A})\boldsymbol {\hat {r}}$, where
$\boldsymbol {c} = (U+v_\textrm {A})\boldsymbol {\hat {r}}$, where ![]() $\boldsymbol {\hat {r}}$ is the radial unit vector and
$\boldsymbol {\hat {r}}$ is the radial unit vector and ![]() $k_r$ is the radial component of the wave vector. In a steady-state solar wind,
$k_r$ is the radial component of the wave vector. In a steady-state solar wind, ![]() $\omega$ depends on neither position nor time. Upon multiplying (3.14) by
$\omega$ depends on neither position nor time. Upon multiplying (3.14) by ![]() $\omega$, integrating over
$\omega$, integrating over ![]() $\omega$, and assuming a steady state, one obtains
$\omega$, and assuming a steady state, one obtains
where
is the total AW energy density,
![]() $\langle \dots \rangle$ indicates a time average,
$\langle \dots \rangle$ indicates a time average,
are the Elsasser variables, ![]() $\delta \boldsymbol {v}$ and
$\delta \boldsymbol {v}$ and ![]() $\delta \boldsymbol {B}$ are the fluctuating velocity and magnetic field, and
$\delta \boldsymbol {B}$ are the fluctuating velocity and magnetic field, and ![]() $\boldsymbol {z}^+$ (
$\boldsymbol {z}^+$ (![]() $\boldsymbol {z}^-$) corresponds to AW fluctuations propagating away from (toward) the Sun.Footnote 1 In (3.17) and the following, a
$\boldsymbol {z}^-$) corresponds to AW fluctuations propagating away from (toward) the Sun.Footnote 1 In (3.17) and the following, a ![]() $\pm$ sign is used as a subscript (as opposed to a superscript) when the subscripted quantity is an r.m.s. value. As
$\pm$ sign is used as a subscript (as opposed to a superscript) when the subscripted quantity is an r.m.s. value. As ![]() ${\boldsymbol{\nabla}\,\boldsymbol{\cdot}}\, (\rho U \boldsymbol {\hat {r}}) = 0$, (3.15) can be rewritten as
${\boldsymbol{\nabla}\,\boldsymbol{\cdot}}\, (\rho U \boldsymbol {\hat {r}}) = 0$, (3.15) can be rewritten as
where
is the wave-action flux per unit mass flux per unit ![]() $\omega$ times
$\omega$ times ![]() $4 \omega$ integrated over
$4 \omega$ integrated over ![]() $\omega$, or, for brevity, the ‘wave action flux per unit mass flux’.
$\omega$, or, for brevity, the ‘wave action flux per unit mass flux’.
When the finite radial wavelength of the AWs is taken into account, the radial gradient in ![]() $v_\textrm {A}$ causes partial non-WKB reflection of
$v_\textrm {A}$ causes partial non-WKB reflection of ![]() $\boldsymbol {z}^+$ fluctuations, leading to the production of
$\boldsymbol {z}^+$ fluctuations, leading to the production of ![]() $\boldsymbol {z}^-$ fluctuations. Counter-propagating AWs then interact, causing fluctuation energy to cascade to small scales and dissipate. In the CH09 model, this loss of fluctuation energy causes
$\boldsymbol {z}^-$ fluctuations. Counter-propagating AWs then interact, causing fluctuation energy to cascade to small scales and dissipate. In the CH09 model, this loss of fluctuation energy causes ![]() $g^2$ to decrease with radius according to the equationFootnote 2
$g^2$ to decrease with radius according to the equationFootnote 2
Equation (3.21) states that in a reference frame that follows an outward-propagating AW, the wave action flux per unit mass flux decays on the eddy turnover time scale ![]() $L_\perp / z_-$. The reason that only
$L_\perp / z_-$. The reason that only ![]() $z_-$ (and not
$z_-$ (and not ![]() $z_+$) appears in this eddy turnover time scale is that
$z_+$) appears in this eddy turnover time scale is that ![]() ${\boldsymbol z}^+$ fluctuations are not sheared or distorted by other
${\boldsymbol z}^+$ fluctuations are not sheared or distorted by other ![]() $\boldsymbol {z}^+$ fluctuations, but they are sheared and distorted by counter-propagating
$\boldsymbol {z}^+$ fluctuations, but they are sheared and distorted by counter-propagating ![]() $\boldsymbol {z}^-$ fluctuations (Iroshnikov Reference Iroshnikov1963; Kraichnan Reference Kraichnan1965). The radial decay of
$\boldsymbol {z}^-$ fluctuations (Iroshnikov Reference Iroshnikov1963; Kraichnan Reference Kraichnan1965). The radial decay of ![]() $g^2$ is accompanied by turbulent heating at the rate
$g^2$ is accompanied by turbulent heating at the rate
which is the energy density of the outward-propagating AWs ![]() $\rho z_+^2 / 4$ divided by their eddy turnover time scale
$\rho z_+^2 / 4$ divided by their eddy turnover time scale ![]() $L_\perp / z_-$. Equation (3.22) drops a term
$L_\perp / z_-$. Equation (3.22) drops a term ![]() $\rho z_-^2 z_+ / (4 L_\perp )$ that is normally included in the turbulent heating rate because of CH09's assumption that
$\rho z_-^2 z_+ / (4 L_\perp )$ that is normally included in the turbulent heating rate because of CH09's assumption that
an inequality that holds in the small-![]() $L_\perp$ limit, as can be seen later in (3.25).
$L_\perp$ limit, as can be seen later in (3.25).
Following D02, CH09 determined ![]() $z_-$ by balancing the rate at which
$z_-$ by balancing the rate at which ![]() $z_-$ is produced through reflections against the rate at which
$z_-$ is produced through reflections against the rate at which ![]() $z_-$ cascades to small scales through nonlinear interactions in the small-
$z_-$ cascades to small scales through nonlinear interactions in the small-![]() $L_\perp$ limit, obtaining
$L_\perp$ limit, obtaining
or, equivalently,
Upon substituting (3.25) into (3.21), assuming that ![]() $v_\textrm {A}(r)$ has a single maximum at
$v_\textrm {A}(r)$ has a single maximum at ![]() $r_\textrm {m} > r_\textrm {b}$, and solving for
$r_\textrm {m} > r_\textrm {b}$, and solving for ![]() $g(r)$, CH09 found that
$g(r)$, CH09 found that
where
 \begin{equation} h(r) = \left\{ \begin{array}{@{}ll} v_\textrm{Ab}/v_\textrm{A}(r) & \mbox{ for } r_\textrm{b} < r < r_\textrm{m} \\ v_\textrm{Ab} v_\textrm{A}(r) / v_\textrm{Am}^2 & \mbox{ if } r > r_\textrm{m} \end{array}\right., \end{equation}
\begin{equation} h(r) = \left\{ \begin{array}{@{}ll} v_\textrm{Ab}/v_\textrm{A}(r) & \mbox{ for } r_\textrm{b} < r < r_\textrm{m} \\ v_\textrm{Ab} v_\textrm{A}(r) / v_\textrm{Am}^2 & \mbox{ if } r > r_\textrm{m} \end{array}\right., \end{equation}
where ![]() $v_\textrm {Am} = v_\textrm {A}(r_\textrm {m})$ is the maximum value of
$v_\textrm {Am} = v_\textrm {A}(r_\textrm {m})$ is the maximum value of ![]() $v_\textrm {A}$. Conceptually, (3.26) and (3.27) state that an appreciable fraction of the local AW action flux per unit mass flux dissipates within each Alfvén-speed scale height, which causes
$v_\textrm {A}$. Conceptually, (3.26) and (3.27) state that an appreciable fraction of the local AW action flux per unit mass flux dissipates within each Alfvén-speed scale height, which causes ![]() $z_+^2(r)$ to drop below the WKB value that would be predicted from (3.20) with constant
$z_+^2(r)$ to drop below the WKB value that would be predicted from (3.20) with constant ![]() $g^2$.
$g^2$.
Upon substituting (3.26) into (3.22) and making use (3.20), CH09 obtained
where
The second equality in (3.29) follows from (3.23). As
equation (3.28) can be rewritten to a good approximation in the following simplified form with the aid of (3.11):
3.2.2. Approximate isothermality between the transition region and Alfvén critical point
In steady state, the plasma internal-energy equation takes the form
where ![]() $p$ is the pressure,
$p$ is the pressure, ![]() $p/(\gamma -1)$ is the internal-energy density,
$p/(\gamma -1)$ is the internal-energy density, ![]() $-p {\boldsymbol{\nabla}\,\boldsymbol{\cdot}}\, \boldsymbol {v}$ is the rate at which
$-p {\boldsymbol{\nabla}\,\boldsymbol{\cdot}}\, \boldsymbol {v}$ is the rate at which ![]() $p\,\textrm {d} V$ work is done on the plasma per unit volume,
$p\,\textrm {d} V$ work is done on the plasma per unit volume, ![]() $Q$ is the rate of turbulent heating per unit volume,
$Q$ is the rate of turbulent heating per unit volume, ![]() $\boldsymbol {q}$ is the heat flux, which is written in the formFootnote 3
$\boldsymbol {q}$ is the heat flux, which is written in the formFootnote 3
and ![]() $R$ is the rate of radiative cooling per unit volume. In the corona and solar wind, the density is sufficiently small that radiative cooling can be neglected, and, to a good approximation, (3.32) can be rewritten with the aid of (3.6) as
$R$ is the rate of radiative cooling per unit volume. In the corona and solar wind, the density is sufficiently small that radiative cooling can be neglected, and, to a good approximation, (3.32) can be rewritten with the aid of (3.6) as
A generic consequence of heating by reflection-driven AW turbulence is that, when other forms of heating (including conduction) are subdominant, the flow becomes quasi-isothermal at ![]() $r_\textrm {b} < r<r_\textrm {A}$, meaning that
$r_\textrm {b} < r<r_\textrm {A}$, meaning that
whereas (3.35) is not satisfied at ![]() $r>r_\textrm {A}$. This can be demonstrated by (1) neglecting conductive heating in (3.34), (2) assuming that (3.35) is satisfied so that the second term on the left-hand side of (3.34) can be neglected, and (3) solving (3.34) for
$r>r_\textrm {A}$. This can be demonstrated by (1) neglecting conductive heating in (3.34), (2) assuming that (3.35) is satisfied so that the second term on the left-hand side of (3.34) can be neglected, and (3) solving (3.34) for ![]() $c_\textrm {s}^2$. If the resulting expression for
$c_\textrm {s}^2$. If the resulting expression for ![]() $c_\textrm {s}(r)^2$ satisfies (3.35), then the neglect of the second term on the left-hand side of (3.34) is self-consistent, and this expression for
$c_\textrm {s}(r)^2$ satisfies (3.35), then the neglect of the second term on the left-hand side of (3.34) is self-consistent, and this expression for ![]() $c_\textrm {s}(r)^2$ is a reasonable approximation for the full solution of (3.34). On the other hand, if the resulting value of
$c_\textrm {s}(r)^2$ is a reasonable approximation for the full solution of (3.34). On the other hand, if the resulting value of ![]() $c_\textrm {s}^2(r)$ does not satisfy (3.35), then (3.34) does not possess a quasi-isothermal solution.
$c_\textrm {s}^2(r)$ does not satisfy (3.35), then (3.34) does not possess a quasi-isothermal solution.
Carrying out this procedure and equating the first term on the left-hand side of (3.34) with the turbulent heating term on the right-hand side (which is given by (3.31)), one obtains
where
are the density and Alfvén-speed scale heights. These scale heights are generally some constant of order unity times ![]() $r$, with
$r$, with ![]() $L_\rho /L_{v_{\textrm {A}}}$ increasing by a factor of a few between the low corona and
$L_\rho /L_{v_{\textrm {A}}}$ increasing by a factor of a few between the low corona and ![]() $r_\textrm {A}$. On the other hand,
$r_\textrm {A}$. On the other hand, ![]() $h(r)$ decreases by a factor of a few between the low corona and
$h(r)$ decreases by a factor of a few between the low corona and ![]() $r_\textrm {A}$, so that the product
$r_\textrm {A}$, so that the product ![]() $(L_\rho/L_{v_{\rm A}})h(r)$ varies quite weakly with
$(L_\rho/L_{v_{\rm A}})h(r)$ varies quite weakly with ![]() $r$.Footnote 4 The
$r$.Footnote 4 The ![]() $v_\textrm {A}/(U+v_\textrm {A})$ term in (3.36) likewise exhibits little variation in the sub-Alfvénic region, ranging from
$v_\textrm {A}/(U+v_\textrm {A})$ term in (3.36) likewise exhibits little variation in the sub-Alfvénic region, ranging from ![]() $\simeq 1$ at
$\simeq 1$ at ![]() $r=r_\textrm {b}$ to
$r=r_\textrm {b}$ to ![]() $0.5$ at
$0.5$ at ![]() $r=r_\textrm {A}$. On the other hand,
$r=r_\textrm {A}$. On the other hand, ![]() $\rho$ varies by a factor of
$\rho$ varies by a factor of ![]() $\sim 10^5$ between the coronal base and
$\sim 10^5$ between the coronal base and ![]() $r_\textrm {A}$ (see, e.g. Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007). Thus, the approximate solution for
$r_\textrm {A}$ (see, e.g. Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007). Thus, the approximate solution for ![]() $c_\textrm {s}^2$ in (3.36) satisfies (3.35) at
$c_\textrm {s}^2$ in (3.36) satisfies (3.35) at ![]() $r_\textrm {b} < r < r_\textrm {A}$, and AW heating indeed causes the sub-Alfvénic region to become quasi-isothermal. In contrast, at
$r_\textrm {b} < r < r_\textrm {A}$, and AW heating indeed causes the sub-Alfvénic region to become quasi-isothermal. In contrast, at ![]() $r>r_\textrm {A}$,
$r>r_\textrm {A}$, ![]() $U$ asymptotes toward a constant value,
$U$ asymptotes toward a constant value, ![]() $h \propto v_\textrm {A} \propto \rho ^{1/2} U \propto \rho ^{1/2}$,
$h \propto v_\textrm {A} \propto \rho ^{1/2} U \propto \rho ^{1/2}$, ![]() $v_\textrm {A}/(U+v_\textrm {A}) \propto \rho ^{1/2}$, and the right-hand side of (3.36) becomes proportional to
$v_\textrm {A}/(U+v_\textrm {A}) \propto \rho ^{1/2}$, and the right-hand side of (3.36) becomes proportional to ![]() $\rho$, contradicting (3.35).
$\rho$, contradicting (3.35).
3.2.3. A modified version of the Chandran & Hollweg (2009) model
There are two difficulties with incorporating the CH09 model into an analytic solar-wind model that includes the region immediately above the transition region. First, (3.25) is consistent with (3.23) only if
The left-hand side of (3.38) is the characteristic distance a ![]() $\boldsymbol {z}^-$ fluctuation at scale
$\boldsymbol {z}^-$ fluctuation at scale ![]() $L_\perp$ (measured perpendicular to the background magnetic field) propagates along the magnetic field before cascading and dissipating, and the right-hand side is the Alfvén-speed scale height. Just above the transition region, the magnetic-field strength has a scale height of order
$L_\perp$ (measured perpendicular to the background magnetic field) propagates along the magnetic field before cascading and dissipating, and the right-hand side is the Alfvén-speed scale height. Just above the transition region, the magnetic-field strength has a scale height of order ![]() $10^{-2} R_{\odot }$ (Hackenberg, Marsch & Mann Reference Hackenberg, Marsch and Mann2000; Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007), the
$10^{-2} R_{\odot }$ (Hackenberg, Marsch & Mann Reference Hackenberg, Marsch and Mann2000; Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007), the ![]() $v_\textrm {A}$ scale height has a similar value, and (3.38) is not satisfied (see, e.g. equation (3.13-a) and table 3 of Chandran & Perez Reference Chandran and Perez2019). On the other hand, beyond the low corona, the
$v_\textrm {A}$ scale height has a similar value, and (3.38) is not satisfied (see, e.g. equation (3.13-a) and table 3 of Chandran & Perez Reference Chandran and Perez2019). On the other hand, beyond the low corona, the ![]() $v_\textrm {A}$ scale height grows to values
$v_\textrm {A}$ scale height grows to values ![]() $\sim r$ that are
$\sim r$ that are ![]() $\gg L_\perp$. Thus, the CH09 model should be applied only beyond some minimum heliocentric distance, and some other approximation is needed to treat the region immediately above the transition region.
$\gg L_\perp$. Thus, the CH09 model should be applied only beyond some minimum heliocentric distance, and some other approximation is needed to treat the region immediately above the transition region.
The second difficulty with incorporating the CH09 model into an analytic solar-wind model is that the function ![]() $h(r)$ in (3.27) depends on the number of local extrema in the Alfvén-speed profile and the locations of these extrema. In models that account for the rapid increase in
$h(r)$ in (3.27) depends on the number of local extrema in the Alfvén-speed profile and the locations of these extrema. In models that account for the rapid increase in ![]() $B(r)$ as
$B(r)$ as ![]() $r$ drops below
$r$ drops below ![]() $\simeq 1.01 R_{\odot }$,
$\simeq 1.01 R_{\odot }$, ![]() $v_\textrm {A}$ typically has two local extrema within the corona: a local minimum just above the coronal base and a local maximum a few tenths of a solar radius above the coronal base. (See, e.g. figure 3 of Cranmer & van Ballegooijen (Reference Cranmer and van Ballegooijen2005) or figure 9 of Cranmer et al. (Reference Cranmer, van Ballegooijen and Edgar2007).) In the context of the analytic solar-wind model developed in the following, each local extremum introduces two new unknowns: the location of the extremum, and either the density or flow speed at the extremum.
$v_\textrm {A}$ typically has two local extrema within the corona: a local minimum just above the coronal base and a local maximum a few tenths of a solar radius above the coronal base. (See, e.g. figure 3 of Cranmer & van Ballegooijen (Reference Cranmer and van Ballegooijen2005) or figure 9 of Cranmer et al. (Reference Cranmer, van Ballegooijen and Edgar2007).) In the context of the analytic solar-wind model developed in the following, each local extremum introduces two new unknowns: the location of the extremum, and either the density or flow speed at the extremum.
In this paper, the first of the two aforementioned difficulties is handled by replacing the CH09 result for ![]() $Q(r)$ at
$Q(r)$ at ![]() $r=r_\textrm {b}$ with the expression
$r=r_\textrm {b}$ with the expression
where ![]() $l_\textrm {b}$ is a free parameter, which is set equal to
$l_\textrm {b}$ is a free parameter, which is set equal to ![]() $0.3 R_{\odot }$ in the numerical examples presented in § 4. The second difficulty is resolved by replacing (3.25) with the expression
$0.3 R_{\odot }$ in the numerical examples presented in § 4. The second difficulty is resolved by replacing (3.25) with the expression
at ![]() $r_\textrm {b} < r < r_\textrm {A}$, where
$r_\textrm {b} < r < r_\textrm {A}$, where ![]() $\sigma$ is a free parameter, whose value is approximately 0.1–0.5 in the numerical examples in § 4. Whereas
$\sigma$ is a free parameter, whose value is approximately 0.1–0.5 in the numerical examples in § 4. Whereas ![]() $z_- / L_\perp = (U+v_\textrm {A})/L_{v_\textrm {A}}$ in (3.25), (3.40) takes
$z_- / L_\perp = (U+v_\textrm {A})/L_{v_\textrm {A}}$ in (3.25), (3.40) takes ![]() $z_- / L_\perp$ to be
$z_- / L_\perp$ to be ![]() $\simeq (U+v_\textrm {A})/L_{\rho }$ times a free parameter.Footnote 5 Because
$\simeq (U+v_\textrm {A})/L_{\rho }$ times a free parameter.Footnote 5 Because ![]() $\rho$ (and, hence,
$\rho$ (and, hence, ![]() $y$) is a monotonically decreasing function of
$y$) is a monotonically decreasing function of ![]() $r$, the minus sign on the right-hand side of (3.40) ensures that
$r$, the minus sign on the right-hand side of (3.40) ensures that ![]() $z_- > 0$. The right-hand side of (3.40) is taken to be proportional to
$z_- > 0$. The right-hand side of (3.40) is taken to be proportional to ![]() $\ln (1+y)$ instead of
$\ln (1+y)$ instead of ![]() $\ln y$ simply to make some of the expressions encountered later on easier to integrate analytically. Another motivation for using (3.40) instead of (3.25) is that the parameter-free CH09 result in (3.25) overestimates the rate at which AWs cascade and dissipate in the solar wind (Chandran & Hollweg Reference Chandran and Hollweg2009), and the introduction of a free parameter in (3.40) in principle makes it possible to correct for this.
$\ln y$ simply to make some of the expressions encountered later on easier to integrate analytically. Another motivation for using (3.40) instead of (3.25) is that the parameter-free CH09 result in (3.25) overestimates the rate at which AWs cascade and dissipate in the solar wind (Chandran & Hollweg Reference Chandran and Hollweg2009), and the introduction of a free parameter in (3.40) in principle makes it possible to correct for this.
Upon substituting (3.40) into (3.21), solving for ![]() $g^2(r)$, and rewriting
$g^2(r)$, and rewriting ![]() $g^2$ in terms of
$g^2$ in terms of ![]() $z_+^2$ using (3.20), one finds that
$z_+^2$ using (3.20), one finds that
Equations (3.22), (3.29), (3.40), and (3.41) can then be used to show that
where
is the total turbulent heating power between ![]() $r_\textrm {b}$ and
$r_\textrm {b}$ and ![]() $r_\textrm {A}$,
$r_\textrm {A}$,
is the power (energy flux times area) of outward-propagating AWs at radius ![]() $r$, and
$r$, and
is the fraction of ![]() $P_\textrm {AW}(r_\textrm {b})$ that is dissipated between
$P_\textrm {AW}(r_\textrm {b})$ that is dissipated between ![]() $r_\textrm {b}$ and
$r_\textrm {b}$ and ![]() $r_\textrm {A}$.
$r_\textrm {A}$.
3.3. Relating the AW amplitudes at the coronal base and photosphere
In the absence of wave reflection and dissipation, ![]() $P_\textrm {AW}$ (defined in (3.44)) would have almost exactly the same value at
$P_\textrm {AW}$ (defined in (3.44)) would have almost exactly the same value at ![]() $r_\textrm {b}$ and
$r_\textrm {b}$ and ![]() $R_{\odot }$.Footnote 6 However, the steep Alfvén-speed gradient in the transition region leads to strong AW reflection, and a vigorous energy cascade in the chromosphere leads to substantial AW dissipation (van Ballegooijen et al. Reference van Ballegooijen, Asgari-Targhi, Cranmer and DeLuca2011; Chandran & Perez Reference Chandran and Perez2019). This reduces
$R_{\odot }$.Footnote 6 However, the steep Alfvén-speed gradient in the transition region leads to strong AW reflection, and a vigorous energy cascade in the chromosphere leads to substantial AW dissipation (van Ballegooijen et al. Reference van Ballegooijen, Asgari-Targhi, Cranmer and DeLuca2011; Chandran & Perez Reference Chandran and Perez2019). This reduces ![]() $P_\textrm {AW}(r_\textrm {b}) / P_\textrm {AW }(R_{\odot })$ to some value
$P_\textrm {AW}(r_\textrm {b}) / P_\textrm {AW }(R_{\odot })$ to some value ![]() $f_\textrm {chr} < 1$, where
$f_\textrm {chr} < 1$, where ![]() $f_\textrm {chr}$ is an effective AW transmission coefficient for the chromosphere and transition region. Equivalently, because
$f_\textrm {chr}$ is an effective AW transmission coefficient for the chromosphere and transition region. Equivalently, because ![]() $U\ll v_\textrm {A}$ at
$U\ll v_\textrm {A}$ at ![]() $r\leqslant r_\textrm {b}$,
$r\leqslant r_\textrm {b}$,
where a ![]() $\odot$ subscript indicates that the subscripted quantity is evaluated at the photosphere. For the numerical calculations in § 4, I set
$\odot$ subscript indicates that the subscripted quantity is evaluated at the photosphere. For the numerical calculations in § 4, I set
As ![]() $B A = \mbox {constant}$ and
$B A = \mbox {constant}$ and ![]() $v_\textrm {A} = B /(4{\rm \pi} \rho )^{1/2}$, (3.46) can be rewritten as
$v_\textrm {A} = B /(4{\rm \pi} \rho )^{1/2}$, (3.46) can be rewritten as
 \begin{equation} \delta v_\textrm{b}^2 = \delta v_{{\odot}\textrm{eff}}^2 \left(\frac{\rho_{{\odot}}}{\rho_\textrm{b}}\right)^{1/2} , \end{equation}
\begin{equation} \delta v_\textrm{b}^2 = \delta v_{{\odot}\textrm{eff}}^2 \left(\frac{\rho_{{\odot}}}{\rho_\textrm{b}}\right)^{1/2} , \end{equation}where
The difference between ![]() $\delta v_{\odot }$ and
$\delta v_{\odot }$ and ![]() $\delta v_{\odot \textrm {eff}}$ is that
$\delta v_{\odot \textrm {eff}}$ is that ![]() $\delta v_{\odot }$ gives rise to the fluctuating velocity
$\delta v_{\odot }$ gives rise to the fluctuating velocity ![]() $\delta v_\textrm {b}$ at
$\delta v_\textrm {b}$ at ![]() $r=r_\textrm {b}$ when reflection and dissipation are accounted for, whereas
$r=r_\textrm {b}$ when reflection and dissipation are accounted for, whereas ![]() $\delta v_{\odot \textrm {eff}}$ would give rise to the same value of
$\delta v_{\odot \textrm {eff}}$ would give rise to the same value of ![]() $\delta v_\textrm {b}$ via WKB propagation (i.e. without reflection or dissipation).
$\delta v_\textrm {b}$ via WKB propagation (i.e. without reflection or dissipation).
The value of ![]() $\delta v_{\odot \textrm {eff}}$ can be constrained in different ways. For example, observations fix
$\delta v_{\odot \textrm {eff}}$ can be constrained in different ways. For example, observations fix ![]() $\delta v_{\odot }$ at a value of
$\delta v_{\odot }$ at a value of ![]() $\simeq 1 \mbox { km} \mbox { s}^{-1}$ (Richardson & Schwarzschild Reference Richardson and Schwarzschild1950), and numerical simulations suggest that
$\simeq 1 \mbox { km} \mbox { s}^{-1}$ (Richardson & Schwarzschild Reference Richardson and Schwarzschild1950), and numerical simulations suggest that ![]() $f_\textrm {chr}$ is
$f_\textrm {chr}$ is ![]() $\simeq 0.04 \text {--} 0.08$ (van Ballegooijen et al. Reference van Ballegooijen, Asgari-Targhi, Cranmer and DeLuca2011; Chandran & Perez Reference Chandran and Perez2019). Alternatively, if the solar wind is assumed to be powered primarily by an AW energy flux, then
$\simeq 0.04 \text {--} 0.08$ (van Ballegooijen et al. Reference van Ballegooijen, Asgari-Targhi, Cranmer and DeLuca2011; Chandran & Perez Reference Chandran and Perez2019). Alternatively, if the solar wind is assumed to be powered primarily by an AW energy flux, then ![]() $\delta v_{\odot \textrm {eff}}$ can be inferred directly from measurements of the mass flux and energy flux far from the Sun. This latter method is used to determine
$\delta v_{\odot \textrm {eff}}$ can be inferred directly from measurements of the mass flux and energy flux far from the Sun. This latter method is used to determine ![]() $\delta v_{\odot \textrm {eff}}$ in some of the numerical solutions presented in § 4 and is described in more detail in § 4.2. It is worth noting that in contrast to
$\delta v_{\odot \textrm {eff}}$ in some of the numerical solutions presented in § 4 and is described in more detail in § 4.2. It is worth noting that in contrast to ![]() $\delta v_{\odot }$,
$\delta v_{\odot }$, ![]() $f_\textrm {chr}$, and
$f_\textrm {chr}$, and ![]() $\delta v_{\odot \textrm {eff}}$, which are plausibly independent of the properties of the coronal plasma and coronal magnetic field,
$\delta v_{\odot \textrm {eff}}$, which are plausibly independent of the properties of the coronal plasma and coronal magnetic field, ![]() $\delta v_\textrm {b}$ depends upon
$\delta v_\textrm {b}$ depends upon ![]() $\rho _\textrm {b}$, which varies between different flux tubes with different super-radial expansion factors
$\rho _\textrm {b}$, which varies between different flux tubes with different super-radial expansion factors ![]() $\eta _\textrm {b}$, as shown later in (3.55).
$\eta _\textrm {b}$, as shown later in (3.55).
3.4. Balancing turbulent heating and radiative cooling at the coronal base
Within the corona and transition region, the plasma is optically thin, and the rate of radiative cooling is given by
where ![]() $m_\textrm {p}$ is the proton mass, and
$m_\textrm {p}$ is the proton mass, and ![]() $\varLambda (T)$ is the optically thin radiative loss function. Figure 2 shows three different approximations to
$\varLambda (T)$ is the optically thin radiative loss function. Figure 2 shows three different approximations to ![]() $\varLambda (T)$. The dashed lines correspond to equation (A1) of Rosner, Tucker & Vaiana (Reference Rosner, Tucker and Vaiana1978). The solid line is a plot of
$\varLambda (T)$. The dashed lines correspond to equation (A1) of Rosner, Tucker & Vaiana (Reference Rosner, Tucker and Vaiana1978). The solid line is a plot of
where
Equation (3.51) is the temperature derivative of equation (A3) of Rosner et al. (Reference Rosner, Tucker and Vaiana1978). The dotted line in figure 2 is a piecewise-continuous linear approximation to the low-temperature range of ![]() $\varLambda (T)$ in figure 1 of Cranmer et al. (Reference Cranmer, van Ballegooijen and Edgar2007), which is included to illustrate that optically thin radiative cooling becomes extremely weak at
$\varLambda (T)$ in figure 1 of Cranmer et al. (Reference Cranmer, van Ballegooijen and Edgar2007), which is included to illustrate that optically thin radiative cooling becomes extremely weak at ![]() $T\lesssim 10^4$ K.
$T\lesssim 10^4$ K.

Figure 2. Three approximations to the optically thin radiative loss function ![]() $\varLambda (T)$; see the text for further discussion.
$\varLambda (T)$; see the text for further discussion.
Throughout most of the corona, ![]() $\rho$ is sufficiently small that radiative cooling is negligible. However, as
$\rho$ is sufficiently small that radiative cooling is negligible. However, as ![]() $r$ decreases within the corona,
$r$ decreases within the corona, ![]() $\rho$ increases by orders of magnitude, which causes
$\rho$ increases by orders of magnitude, which causes ![]() $R/Q$ to increase, because
$R/Q$ to increase, because ![]() $R\propto \rho ^2$. There is thus some radius
$R\propto \rho ^2$. There is thus some radius ![]() $r_\textrm {b}$ at which
$r_\textrm {b}$ at which
which marks the transition between the corona, in which radiative cooling is negligible, and the low solar atmosphere, in which radiation is thermodynamically important. In this paper, the radius ![]() $r_\textrm {b}$ is identified as the base of the corona, as already noted in (3.1). As
$r_\textrm {b}$ is identified as the base of the corona, as already noted in (3.1). As ![]() $r$ decreases below
$r$ decreases below ![]() $r_\textrm {b}$,
$r_\textrm {b}$, ![]() $\rho (r)$ increases above
$\rho (r)$ increases above ![]() $\rho _\textrm {b}$,
$\rho _\textrm {b}$, ![]() $R/Q$ increases to values
$R/Q$ increases to values ![]() $\gg 1$, and the temperature gradient length scale must decrease so that conductive heating can balance radiative cooling (as well as internal-energy losses from advection and
$\gg 1$, and the temperature gradient length scale must decrease so that conductive heating can balance radiative cooling (as well as internal-energy losses from advection and ![]() $p\,\textrm {d} V$ work). This shortening of the temperature gradient length scale gives rise to the transition region, which is discussed further in § 3.6. To facilitate an analytic solution, I neglect turbulent heating at
$p\,\textrm {d} V$ work). This shortening of the temperature gradient length scale gives rise to the transition region, which is discussed further in § 3.6. To facilitate an analytic solution, I neglect turbulent heating at ![]() $r<r_\textrm {b}$ and radiative cooling at
$r<r_\textrm {b}$ and radiative cooling at ![]() $r>r_\textrm {b}$.
$r>r_\textrm {b}$.
With the aid of (3.39), (3.46), and (3.50), (3.53) can be written in the form
Solving for ![]() $\rho _\textrm {b}$, one finds via (3.51) that
$\rho _\textrm {b}$, one finds via (3.51) that
 \begin{equation} \rho_\textrm{b} = \left(\frac{\delta v_{{\odot}\textrm{eff}}^2 \psi \bar{B} \eta_\textrm{b} m_\textrm{p}^{5/2} \overline{c_\textrm{s}}}{c_\textrm{R} l_\textrm{b}}\right)^{1/2} \left(\frac{\rho_{{\odot}}}{8 {\rm \pi}k_\textrm{B}}\right)^{1/4}, \end{equation}
\begin{equation} \rho_\textrm{b} = \left(\frac{\delta v_{{\odot}\textrm{eff}}^2 \psi \bar{B} \eta_\textrm{b} m_\textrm{p}^{5/2} \overline{c_\textrm{s}}}{c_\textrm{R} l_\textrm{b}}\right)^{1/2} \left(\frac{\rho_{{\odot}}}{8 {\rm \pi}k_\textrm{B}}\right)^{1/4}, \end{equation}where
is the sound speed (2.6) in the sub-Alfvénic region (![]() $r_\textrm {b} < r < r_\textrm {A}$), which is approximated as a constant for the reasons discussed in § 3.2.2. Equation (3.55) can be rewritten as
$r_\textrm {b} < r < r_\textrm {A}$), which is approximated as a constant for the reasons discussed in § 3.2.2. Equation (3.55) can be rewritten as
where
is the dimensionless temperature of the sub-Alfvénic region,
 \begin{equation} B_\textrm{ref} = \left(\frac{4 {\rm \pi}m_\textrm{p}^{5/2} v_\textrm{esc}^6}{c_\textrm{R} R_{{\odot}} \sqrt{2 k_\textrm{B }}}\right)^{1/2} = 118.8 \mbox{ G} \end{equation}
\begin{equation} B_\textrm{ref} = \left(\frac{4 {\rm \pi}m_\textrm{p}^{5/2} v_\textrm{esc}^6}{c_\textrm{R} R_{{\odot}} \sqrt{2 k_\textrm{B }}}\right)^{1/2} = 118.8 \mbox{ G} \end{equation}
is the magnetic-field strength for which ![]() $v_\textrm {A} = v_\textrm {esc}$ when the radiative cooling time
$v_\textrm {A} = v_\textrm {esc}$ when the radiative cooling time ![]() $\rho \overline { c_\textrm {s}}^2 / R$, free-fall time
$\rho \overline { c_\textrm {s}}^2 / R$, free-fall time ![]() $R_{\odot }/v_\textrm {esc}$, and sound-crossing time
$R_{\odot }/v_\textrm {esc}$, and sound-crossing time ![]() $R_{\odot }/\overline {c_\textrm {s}}$ are all equal,
$R_{\odot }/\overline {c_\textrm {s}}$ are all equal,
(for reference, ![]() $\tilde {\rho }_\odot = 5.7 \times 10^5$ given (3.47)), and
$\tilde {\rho }_\odot = 5.7 \times 10^5$ given (3.47)), and
 \begin{equation} \xi = \left(\frac{\epsilon_{{\odot}} \eta_\textrm{b}}{B_\ast^3 \tilde{l}_\textrm{b}}\right)^{1/4} \qquad B_\ast\ {=}\ \frac{\bar{B}}{B_\textrm{ref}} \qquad \tilde{l}_\textrm{b} = \frac{l_\textrm{b}}{R_{{\odot}}}. \end{equation}
\begin{equation} \xi = \left(\frac{\epsilon_{{\odot}} \eta_\textrm{b}}{B_\ast^3 \tilde{l}_\textrm{b}}\right)^{1/4} \qquad B_\ast\ {=}\ \frac{\bar{B}}{B_\textrm{ref}} \qquad \tilde{l}_\textrm{b} = \frac{l_\textrm{b}}{R_{{\odot}}}. \end{equation}
Equation (3.57) can used to express ![]() $v_\textrm {Ab}$ in the form
$v_\textrm {Ab}$ in the form
and (3.48), (3.57), and (3.60) can be used to write
3.5. Internal-energy equilibrium within the sub-Alfvénic region
In the quasi-isothermal approximation (3.35), the second term on the left-hand side of (3.34) is negligible, and the volume integral of (3.34) between ![]() $r=r_\textrm {b}$ and
$r=r_\textrm {b}$ and ![]() $r=r_\textrm {A}$ yields
$r=r_\textrm {A}$ yields
where (3.42)–(3.44) have been used to rewrite the volume integral of the turbulent heating rate, (3.8) has been used to pull a constant factor of ![]() $\dot {M} = \rho A U$ out of the integral on the left-hand side, and (3.11) has been used to write
$\dot {M} = \rho A U$ out of the integral on the left-hand side, and (3.11) has been used to write ![]() $U_\textrm {b} + v_\textrm {Ab} = U_\textrm {b} (1 + y_\textrm {b})$.
$U_\textrm {b} + v_\textrm {Ab} = U_\textrm {b} (1 + y_\textrm {b})$.
The heat flux at ![]() $r=r_\textrm {A}$ is a small fraction of the total energy flux in AW-driven solar-wind models and is thus neglected in (3.65). Upon evaluating the integral on the left-hand side of (3.65), noting that
$r=r_\textrm {A}$ is a small fraction of the total energy flux in AW-driven solar-wind models and is thus neglected in (3.65). Upon evaluating the integral on the left-hand side of (3.65), noting that ![]() $q_{r\textrm {b}} = - |q_{r \textrm {b}}| \equiv - q_\textrm {b}$, making use of (3.12), and rearranging terms, one obtains
$q_{r\textrm {b}} = - |q_{r \textrm {b}}| \equiv - q_\textrm {b}$, making use of (3.12), and rearranging terms, one obtains
The left-hand side of (3.66) is the total turbulent heating rate within the sub-Alfvénic region, which represents the source of internal energy between ![]() $r_\textrm {b}$ and
$r_\textrm {b}$ and ![]() $r_\textrm {A}$. The two terms on the right-hand side of (3.66) are the dominant sinks of internal energy in the sub-Alfvénic region:
$r_\textrm {A}$. The two terms on the right-hand side of (3.66) are the dominant sinks of internal energy in the sub-Alfvénic region: ![]() $p\,\textrm {d} V$ work and thermal conduction into the transition region. Dividing (3.66) by
$p\,\textrm {d} V$ work and thermal conduction into the transition region. Dividing (3.66) by ![]() $\dot {M} v_\textrm {esc}^2$ leads to
$\dot {M} v_\textrm {esc}^2$ leads to
3.6. The flux of heat from the corona into the transition region
The temperature structure within the transition region can be determined using a method similar to the methods of Rosner et al. (Reference Rosner, Tucker and Vaiana1978) and Schwadron & McComas (Reference Schwadron and McComas2003). The Knudsen number ![]() $N_\textrm {K}$ (the electron Coulomb mean free path
$N_\textrm {K}$ (the electron Coulomb mean free path ![]() $\lambda _\textrm {mfp}$ divided by the temperature gradient scale length
$\lambda _\textrm {mfp}$ divided by the temperature gradient scale length ![]() $l_T$) is approximately
$l_T$) is approximately ![]() $10^{-3}$ in the low corona, approximately
$10^{-3}$ in the low corona, approximately ![]() $10^{-3}$ at the upper end of the transition region, and approximately
$10^{-3}$ at the upper end of the transition region, and approximately ![]() $10^{-6}$ at the lower end of the transition region.Footnote 7 Because
$10^{-6}$ at the lower end of the transition region.Footnote 7 Because ![]() $N_\textrm {K} \ll 1$, the radial component of the heat flux in the transition region is well approximated by the Spitzer & Härm (Reference Spitzer and Härm1953) formula,
$N_\textrm {K} \ll 1$, the radial component of the heat flux in the transition region is well approximated by the Spitzer & Härm (Reference Spitzer and Härm1953) formula,
where
and ![]() $\ln \varLambda _\textrm {Coul}$ is the Coulomb logarithm. In the numerical examples of § 4,
$\ln \varLambda _\textrm {Coul}$ is the Coulomb logarithm. In the numerical examples of § 4,
the value for electron-electron collisions in a proton-electron plasma with ![]() $\rho /m_\textrm {p} = 10^{9} \mbox { cm}^{-3}$ and
$\rho /m_\textrm {p} = 10^{9} \mbox { cm}^{-3}$ and ![]() $T = 10^6 \mbox { K}$ (Huba Reference Huba2013). The magnetic field near
$T = 10^6 \mbox { K}$ (Huba Reference Huba2013). The magnetic field near ![]() $r=r_\textrm {b}$ is taken to be approximately radial, and the width of the transition region (
$r=r_\textrm {b}$ is taken to be approximately radial, and the width of the transition region (![]() $\sim 10^2 \mbox { km}$) is so narrow that
$\sim 10^2 \mbox { km}$) is so narrow that ![]() $p$,
$p$, ![]() $B$, and
$B$, and ![]() $A$ are treated as constants within the transition region, with
$A$ are treated as constants within the transition region, with
As mentioned previously, turbulent heating is neglected at ![]() $r< r_\textrm {b}$. Within the transition region, (3.32) thus becomes
$r< r_\textrm {b}$. Within the transition region, (3.32) thus becomes
where ![]() $\rho$ has been expressed in terms of
$\rho$ has been expressed in terms of ![]() $p$ and
$p$ and ![]() $T$ using (2.6). The velocity divergence in (3.72) can be expressed in terms of the heat flux via
$T$ using (2.6). The velocity divergence in (3.72) can be expressed in terms of the heat flux via
where the first equality follows from (3.6). With the aid of (3.73), and using (3.68) to write
one can rewrite (3.72) in the form
where
are both constants. Upon defining
which is positive, one can rewrite (3.75) as
which can be integrated from the chromospheric values of ![]() $T$ and
$T$ and ![]() $w$, denoted
$w$, denoted ![]() $T_\textrm {chr}$ and
$T_\textrm {chr}$ and ![]() $w_\textrm {chr}$, to the values of
$w_\textrm {chr}$, to the values of ![]() $T$ and
$T$ and ![]() $w$ at
$w$ at ![]() $r=r_\textrm {b}$, denoted
$r=r_\textrm {b}$, denoted ![]() $T_\textrm {b}$ and
$T_\textrm {b}$ and ![]() $w_\textrm {b}$. As
$w_\textrm {b}$. As ![]() $T_\textrm {chr} \ll T_\textrm {b}$ and the chromospheric heat flux is negligible (
$T_\textrm {chr} \ll T_\textrm {b}$ and the chromospheric heat flux is negligible (![]() $q$ scaling as
$q$ scaling as ![]() $T^{7/2}$ divided by the temperature-gradient scale length), the chromospheric terms are dropped, and the integral becomes
$T^{7/2}$ divided by the temperature-gradient scale length), the chromospheric terms are dropped, and the integral becomes
where
 \begin{gather} I_1 = \left(\frac{\alpha c_\textrm{R} m_\textrm{p}}{4 k_\textrm{B}^3}\right)^{1/2} = 0.1581, \end{gather}
\begin{gather} I_1 = \left(\frac{\alpha c_\textrm{R} m_\textrm{p}}{4 k_\textrm{B}^3}\right)^{1/2} = 0.1581, \end{gather}
and the numerical value on the right-hand side of (3.81) is calculated using (3.70). Equation (3.79) can be solved in terms of the lower branch of the Lambert ![]() $W$ function,
$W$ function, ![]() $W_{-1}$. This solution, in conjunction with (3.77), yields
$W_{-1}$. This solution, in conjunction with (3.77), yields
which is positive since ![]() $\displaystyle W_{-1}(- e^{-(1+a_3)})<-1$.
$\displaystyle W_{-1}(- e^{-(1+a_3)})<-1$.
If ![]() $U_\textrm {b}/ \overline { c_\textrm {s}}$ is sufficiently small, then
$U_\textrm {b}/ \overline { c_\textrm {s}}$ is sufficiently small, then ![]() $a_3 \ll 1$. In this low-Mach-number limit, (3.82) becomes, to leading order in
$a_3 \ll 1$. In this low-Mach-number limit, (3.82) becomes, to leading order in ![]() $a_3$,
$a_3$,
Equation (3.83) is equivalent to equation (3.15) of Rosner et al. (Reference Rosner, Tucker and Vaiana1978) when thermal conduction is the only source of heating in the transition region, i.e. when ![]() $f_\textrm {H}$ is set equal to zero in their equation (3.15). Equation (3.82) follows Schwadron & McComas (Reference Schwadron and McComas2003) in generalising the work of Rosner et al. (Reference Rosner, Tucker and Vaiana1978) to include internal-energy losses from
$f_\textrm {H}$ is set equal to zero in their equation (3.15). Equation (3.82) follows Schwadron & McComas (Reference Schwadron and McComas2003) in generalising the work of Rosner et al. (Reference Rosner, Tucker and Vaiana1978) to include internal-energy losses from ![]() $p\,\textrm {d} V$ work and advection. However, the analysis leading to (3.82) differs from that of Schwadron & McComas (Reference Schwadron and McComas2003) in that (3.82) completely neglects turbulent heating at
$p\,\textrm {d} V$ work and advection. However, the analysis leading to (3.82) differs from that of Schwadron & McComas (Reference Schwadron and McComas2003) in that (3.82) completely neglects turbulent heating at ![]() $r<r_\textrm {b}$ and does not assume that
$r<r_\textrm {b}$ and does not assume that ![]() $\int q(T) \,\textrm {d} T \propto T$.Footnote 8
$\int q(T) \,\textrm {d} T \propto T$.Footnote 8
3.7. Constraints associated with the wave-modified sonic critical point
In the presence of mostly outward-propagating AWs, a radial background magnetic field, and a radial outflow, the momentum equation in the approximately isothermal sub-Alfvénic region takes the form
where ![]() $\rho z_+^2 / 8$ is the AW pressure, which is one-half the AW energy density (Dewar Reference Dewar1970). Equation (3.7) implies that
$\rho z_+^2 / 8$ is the AW pressure, which is one-half the AW energy density (Dewar Reference Dewar1970). Equation (3.7) implies that
Equations (3.41) and (3.85) can be used to rewrite (3.84) in the form
where
and ![]() $\eta$ is defined in (3.2). In order for (3.86) to possess a transonic-wind solution for
$\eta$ is defined in (3.2). In order for (3.86) to possess a transonic-wind solution for ![]() $U$, the quantity in braces on the left-hand side must be positive near the Sun and negative far from the Sun; i.e. it must pass through zero at some radius
$U$, the quantity in braces on the left-hand side must be positive near the Sun and negative far from the Sun; i.e. it must pass through zero at some radius ![]() $r_\textrm {c}$ (the wave-modified sonic critical point). In order for
$r_\textrm {c}$ (the wave-modified sonic critical point). In order for ![]() $\textrm {d} \rho / \textrm {d} r$ to remain finite at
$\textrm {d} \rho / \textrm {d} r$ to remain finite at ![]() $r=r_\textrm {c}$, the right-hand side of (3.86) must also vanish at
$r=r_\textrm {c}$, the right-hand side of (3.86) must also vanish at ![]() $r_\textrm {c}$. Together, these conditions yield the constraints
$r_\textrm {c}$. Together, these conditions yield the constraints
and
where, here and in the following, a ‘c’ subscript indicates that the subscripted quantity is evaluated at ![]() $r=r_\textrm {c}$. An implicit assumption underlying (3.88) and (3.89) is that
$r=r_\textrm {c}$. An implicit assumption underlying (3.88) and (3.89) is that
so that the quasi-isothermal approximation applies at ![]() $r_\textrm {c}$.
$r_\textrm {c}$.
Mass and flux conservation (i.e. (3.7)) imply that
where the second equality in (3.91) follows from (3.11). Equation (3.2) implies that
where the second equality in (3.92) follows from (3.88). Upon substituting (3.92) into (3.91) and evaluating ![]() $v_\textrm {Ab}$ using (3.63), one obtains
$v_\textrm {Ab}$ using (3.63), one obtains
 \begin{equation} U_\textrm{c}^2 = v_\textrm{esc}^2 \left[\frac{y_\textrm{c}^2 \psi^{1/4} \xi (x \tilde{\rho}_{{\odot}})^{1/8}}{16 \gamma_{B{\rm c}}^2 \eta_\textrm{c} y_\textrm{b}}\right]^{2/3}. \end{equation}
\begin{equation} U_\textrm{c}^2 = v_\textrm{esc}^2 \left[\frac{y_\textrm{c}^2 \psi^{1/4} \xi (x \tilde{\rho}_{{\odot}})^{1/8}}{16 \gamma_{B{\rm c}}^2 \eta_\textrm{c} y_\textrm{b}}\right]^{2/3}. \end{equation}Substituting (3.93) into (3.89) yields
 \begin{equation} \left[\frac{y_\textrm{c}^2 \psi^{1/4} \xi (x \tilde{\rho}_{{\odot}})^{1/8}}{16 \gamma_{B{\rm c}}^2 \eta_\textrm{c} y_\textrm{b}}\right]^{2/3} - x - \frac{\epsilon (1+y_\textrm{b})^{2-\sigma}[y_\textrm{c}^2(1+\sigma) + 3 y_\textrm{c}]}{4 y_\textrm{b}(1+y_\textrm{c})^{3-\sigma}} = 0. \end{equation}
\begin{equation} \left[\frac{y_\textrm{c}^2 \psi^{1/4} \xi (x \tilde{\rho}_{{\odot}})^{1/8}}{16 \gamma_{B{\rm c}}^2 \eta_\textrm{c} y_\textrm{b}}\right]^{2/3} - x - \frac{\epsilon (1+y_\textrm{b})^{2-\sigma}[y_\textrm{c}^2(1+\sigma) + 3 y_\textrm{c}]}{4 y_\textrm{b}(1+y_\textrm{c})^{3-\sigma}} = 0. \end{equation} The integral over ![]() $r$ of
$r$ of ![]() $\rho ^{-1}$ times the momentum equation (3.84) yields the Bernoulli integral,
$\rho ^{-1}$ times the momentum equation (3.84) yields the Bernoulli integral,
where ![]() $\varGamma$ is independent of
$\varGamma$ is independent of ![]() $r$. Evaluating (3.95) at
$r$. Evaluating (3.95) at ![]() $r=r_\textrm {b}$ leads to the equality
$r=r_\textrm {b}$ leads to the equality
Evaluating (3.95) at ![]() $r=r_\textrm {c}$, rewriting
$r=r_\textrm {c}$, rewriting ![]() $r_\textrm {c}$ and
$r_\textrm {c}$ and ![]() $U_\textrm {c}$ using (3.88) and (3.89), rewriting
$U_\textrm {c}$ using (3.88) and (3.89), rewriting ![]() $\varGamma$ using (3.96), and multiplying the resulting equation by
$\varGamma$ using (3.96), and multiplying the resulting equation by ![]() $2/v_\textrm {esc}^2$ yields
$2/v_\textrm {esc}^2$ yields
 \begin{align} &\psi^{1/2} + x\left[4 \ln\left( \frac{y_\textrm{c}}{y_\textrm{b}}\right) + 1 - 4 \gamma_{B{\rm c}}\right] + \frac{\epsilon (1 + y_\textrm{b})^{2-\sigma} \varPhi}{4 (1-\sigma)y_\textrm{b} (1+y_\textrm{c})^{3-\sigma}}\nonumber\\ &\quad - \frac{\eta_\textrm{b}^2 \psi^{3/2}}{y_\textrm{b}^2 \xi^2 (x \tilde{\rho}_{{\odot}})^{1/4}} + \epsilon \left[\frac{1+\sigma}{1-\sigma} + \frac{2}{y_\textrm{b}(1-\sigma)}\right] = 0 , \end{align}
\begin{align} &\psi^{1/2} + x\left[4 \ln\left( \frac{y_\textrm{c}}{y_\textrm{b}}\right) + 1 - 4 \gamma_{B{\rm c}}\right] + \frac{\epsilon (1 + y_\textrm{b})^{2-\sigma} \varPhi}{4 (1-\sigma)y_\textrm{b} (1+y_\textrm{c})^{3-\sigma}}\nonumber\\ &\quad - \frac{\eta_\textrm{b}^2 \psi^{3/2}}{y_\textrm{b}^2 \xi^2 (x \tilde{\rho}_{{\odot}})^{1/4}} + \epsilon \left[\frac{1+\sigma}{1-\sigma} + \frac{2}{y_\textrm{b}(1-\sigma)}\right] = 0 , \end{align}where
3.8. Mathematical structure of the model and approximate analytic solutions
The various quantities appearing in the model equations can be divided into five groups: (1) quantities that are determined observationally (![]() $R_{\odot }$,
$R_{\odot }$, ![]() $M_{\odot }$,
$M_{\odot }$, ![]() $v_\textrm {esc}$,
$v_\textrm {esc}$, ![]() $\rho _{\odot }$,
$\rho _{\odot }$, ![]() $\tilde {\rho }_{\odot }$,
$\tilde {\rho }_{\odot }$, ![]() $\psi$,
$\psi$, ![]() $\delta v_{\odot \textrm {eff}}$,
$\delta v_{\odot \textrm {eff}}$, ![]() $\bar {B}$); (2) free parameters (
$\bar {B}$); (2) free parameters (![]() $\sigma$,
$\sigma$, ![]() $l_\textrm {b}$); (3) the super-radial expansion factor
$l_\textrm {b}$); (3) the super-radial expansion factor ![]() $\eta (r)$, which takes on different values in different magnetic flux tubes and in different models for the solar magnetic field; (4) the three principal unknowns,
$\eta (r)$, which takes on different values in different magnetic flux tubes and in different models for the solar magnetic field; (4) the three principal unknowns, ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$; and (5) additional unknowns that can be determined once
$x$; and (5) additional unknowns that can be determined once ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$ are found (
$x$ are found (![]() $\dot {M}$,
$\dot {M}$, ![]() $\chi _\textrm {H}$,
$\chi _\textrm {H}$, ![]() $U(r)$,
$U(r)$, ![]() $\rho _\textrm {b}$,
$\rho _\textrm {b}$, ![]() $q_\textrm {b}$,
$q_\textrm {b}$, ![]() $v_\textrm {Ab}$,
$v_\textrm {Ab}$, ![]() $r_\textrm {c}$,
$r_\textrm {c}$, ![]() $r_\textrm {A}$). The three principal unknowns
$r_\textrm {A}$). The three principal unknowns ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$ are determined by solving the three simultaneous equations (3.67), (3.94), and (3.97), where it must be remembered that
$x$ are determined by solving the three simultaneous equations (3.67), (3.94), and (3.97), where it must be remembered that ![]() $\epsilon$ is itself a function of
$\epsilon$ is itself a function of ![]() $x$ via (3.64). The additional unknowns
$x$ via (3.64). The additional unknowns ![]() $\dot {M}$,
$\dot {M}$, ![]() $\chi _\textrm {H}$,
$\chi _\textrm {H}$, ![]() $\rho _\textrm {b}$,
$\rho _\textrm {b}$, ![]() $v_\textrm {Ab}$,
$v_\textrm {Ab}$, ![]() $q_\textrm {b}$, and
$q_\textrm {b}$, and ![]() $r_\textrm {c}$ then follow immediately from (3.13), (3.45), (3.57), (3.63), (3.82), and (3.88), respectively. For example,
$r_\textrm {c}$ then follow immediately from (3.13), (3.45), (3.57), (3.63), (3.82), and (3.88), respectively. For example,
The procedures for determining ![]() $r_\textrm {A}$ and
$r_\textrm {A}$ and ![]() $U(r)$ involve a few more steps, which are described in Appendix A.
$U(r)$ involve a few more steps, which are described in Appendix A.
Two approximate analytic solutions to (3.67), (3.94) and (3.97), valid in two different parameter regimes, are derived in Appendix B. Both solutions rely on the approximations
The last equality in (3.100) amounts to taking the magnetic-field lines to be purely radial at ![]() $r\geqslant r_\textrm {c}$. The first of the two approximate analytic solutions is valid in the conduction-dominated regime, in which the dominant sink of internal energy in the sub-Alfvénic region is the flux of heat from the corona into the transition region, rather than
$r\geqslant r_\textrm {c}$. The first of the two approximate analytic solutions is valid in the conduction-dominated regime, in which the dominant sink of internal energy in the sub-Alfvénic region is the flux of heat from the corona into the transition region, rather than ![]() $p\,\textrm {d} V$ work. As discussed further in the following, this regime arises only for values of
$p\,\textrm {d} V$ work. As discussed further in the following, this regime arises only for values of ![]() $\delta v_{\odot \textrm {eff}}$ much smaller than the solar value. This limit is thus not directly relevant to solar-wind observations. To leading order in
$\delta v_{\odot \textrm {eff}}$ much smaller than the solar value. This limit is thus not directly relevant to solar-wind observations. To leading order in ![]() $\epsilon _\odot$, the mass outflow rate
$\epsilon _\odot$, the mass outflow rate ![]() $\dot {M}^\textrm {(cond)}$ and asymptotic flow velocity
$\dot {M}^\textrm {(cond)}$ and asymptotic flow velocity ![]() $U_{\infty }^\textrm {(cond)}$ in this parameter regime are given by
$U_{\infty }^\textrm {(cond)}$ in this parameter regime are given by
 \begin{equation} \dot{M}^\textrm{(cond)}=\frac{R_{{\odot}}^2 B_\textrm{ref}^2}{v_\textrm{esc}} \frac{1}{I_1^{1/14} I_2} [ \epsilon_\odot^{14-4\sigma} (\eta_\textrm{b} B_\ast)^{{-}4\sigma} \tilde{l}_\textrm{b}^{3\sigma}\tilde{\rho}_\odot^{7-2\sigma}]^{1/(7-7\sigma)}, \end{equation}
\begin{equation} \dot{M}^\textrm{(cond)}=\frac{R_{{\odot}}^2 B_\textrm{ref}^2}{v_\textrm{esc}} \frac{1}{I_1^{1/14} I_2} [ \epsilon_\odot^{14-4\sigma} (\eta_\textrm{b} B_\ast)^{{-}4\sigma} \tilde{l}_\textrm{b}^{3\sigma}\tilde{\rho}_\odot^{7-2\sigma}]^{1/(7-7\sigma)}, \end{equation}
where ![]() $I_2$ is a numerical constant given in (B 12), and
$I_2$ is a numerical constant given in (B 12), and
 \begin{align} U_\infty^\textrm{(cond)} &= v_\textrm{esc}\Bigg[ \frac{2^{9-4\sigma} \zeta} {(1+\sigma)^2 I_1^{\sigma/14}} \left( \frac{1-\sigma}{7-3\sigma}\right)^{(7-3\sigma)/2}\nonumber\\ &\quad\vphantom{ \frac{2^{9-4\sigma} \zeta} {(1+\sigma)^2 I_1^{\sigma/14}}}\epsilon_\odot^{-(7-2\sigma)/7} B_\ast^{(7-5\sigma)/7} \eta_\textrm{b}^{2\sigma/7} \tilde{\rho}_\odot^{({-}7 + 2 \sigma)/14} \tilde{l}_\textrm{b}^{{-}3\sigma/14}\Bigg]^{1/2}. \end{align}
\begin{align} U_\infty^\textrm{(cond)} &= v_\textrm{esc}\Bigg[ \frac{2^{9-4\sigma} \zeta} {(1+\sigma)^2 I_1^{\sigma/14}} \left( \frac{1-\sigma}{7-3\sigma}\right)^{(7-3\sigma)/2}\nonumber\\ &\quad\vphantom{ \frac{2^{9-4\sigma} \zeta} {(1+\sigma)^2 I_1^{\sigma/14}}}\epsilon_\odot^{-(7-2\sigma)/7} B_\ast^{(7-5\sigma)/7} \eta_\textrm{b}^{2\sigma/7} \tilde{\rho}_\odot^{({-}7 + 2 \sigma)/14} \tilde{l}_\textrm{b}^{{-}3\sigma/14}\Bigg]^{1/2}. \end{align}The coronal temperature in the conduction-dominated limit follows directly from (2.6) and (B 8).
The second approximate analytic solution is valid in the expansion-dominated regime, in which the ![]() $p\,\textrm {d} V$ work resulting from expansion is the dominant sink of internal energy in the sub-Alfvénic region. To leading order, the mass outflow rate in this parameter regime is given by
$p\,\textrm {d} V$ work resulting from expansion is the dominant sink of internal energy in the sub-Alfvénic region. To leading order, the mass outflow rate in this parameter regime is given by
where ![]() $P_\textrm {AW}(r_\textrm {b})$ is the AW power (3.44) evaluated at the coronal base. The asymptotic wind speed in the expansion-dominated regime is to leading order given by
$P_\textrm {AW}(r_\textrm {b})$ is the AW power (3.44) evaluated at the coronal base. The asymptotic wind speed in the expansion-dominated regime is to leading order given by
and the coronal temperature in the expansion-dominated regime is to leading order
 \begin{equation} T = \frac{m_\textrm{p} v_\textrm{esc}^2}{k_\textrm{B} \ln(\epsilon_\odot^{{-}3} \tilde{\rho}_{{\odot}}^{{-}3/2} \tilde{l}_\textrm{b}^{{-}1} \eta_\textrm{b} B_\ast)}. \end{equation}
\begin{equation} T = \frac{m_\textrm{p} v_\textrm{esc}^2}{k_\textrm{B} \ln(\epsilon_\odot^{{-}3} \tilde{\rho}_{{\odot}}^{{-}3/2} \tilde{l}_\textrm{b}^{{-}1} \eta_\textrm{b} B_\ast)}. \end{equation}
Equations (3.103) and (3.104) reproduce the approximate scalings of the simplified calculation presented in § 2. Equation (3.105) matches the right-hand side of (2.19) to within five percent for Sun-like parameters, the difference arising because in the model developed in this section, ![]() $\delta v_\textrm {b}$ has a weak dependence on the coronal temperature via (3.48) and (3.57) that is not accounted for in § 2. Appendix B presents higher-order corrections to (3.103), (3.104), and (3.105) that account for conductive losses, wave momentum deposition inside the wave-modified sonic critical point, and the fact that only part of
$\delta v_\textrm {b}$ has a weak dependence on the coronal temperature via (3.48) and (3.57) that is not accounted for in § 2. Appendix B presents higher-order corrections to (3.103), (3.104), and (3.105) that account for conductive losses, wave momentum deposition inside the wave-modified sonic critical point, and the fact that only part of ![]() $P_\textrm {AW}(r_\textrm {b})$ is dissipated within the sub-Alfvénic region. Second- and fourth-order approximations to
$P_\textrm {AW}(r_\textrm {b})$ is dissipated within the sub-Alfvénic region. Second- and fourth-order approximations to ![]() $\dot {M}$ and
$\dot {M}$ and ![]() $U_\infty$ are shown in figure 5 below.
$U_\infty$ are shown in figure 5 below.
Analytic estimates for the ranges of ![]() $\epsilon _{\odot }$ values corresponding to the conduction-dominated and expansion-dominated limits are given in Appendix B. There are three constraints on
$\epsilon _{\odot }$ values corresponding to the conduction-dominated and expansion-dominated limits are given in Appendix B. There are three constraints on ![]() $\epsilon _\odot$ in the conduction-dominated limit, the most stringent of which is that the wave-energy term dominates over the internal-energy term in the Bernoulli integral at the wave-modified sonic critical point. The resulting range of
$\epsilon _\odot$ in the conduction-dominated limit, the most stringent of which is that the wave-energy term dominates over the internal-energy term in the Bernoulli integral at the wave-modified sonic critical point. The resulting range of ![]() $\epsilon _\odot$ values is much smaller than the solar value, as illustrated in figure 4. The expansion-dominated limit corresponds to a finite range of
$\epsilon _\odot$ values is much smaller than the solar value, as illustrated in figure 4. The expansion-dominated limit corresponds to a finite range of ![]() $\epsilon _\odot$ values that is sufficiently large that
$\epsilon _\odot$ values that is sufficiently large that ![]() $p\,\textrm {d} V$ work dominates over conduction as the primary internal-energy sink within the sub-Alfvénic region, and sufficiently small that the sound speed makes the dominant contribution to the outflow velocity at the wave-modified sonic point in (3.89). This range of
$p\,\textrm {d} V$ work dominates over conduction as the primary internal-energy sink within the sub-Alfvénic region, and sufficiently small that the sound speed makes the dominant contribution to the outflow velocity at the wave-modified sonic point in (3.89). This range of ![]() $\epsilon _\odot$ values is relevant to the solar case, as shown in the next section.
$\epsilon _\odot$ values is relevant to the solar case, as shown in the next section.
4. Numerical examples
This section presents several numerical solutions and approximate analytic solutions to the equations of the model developed in § 3. The numerical solutions are obtained by solving (3.67), (3.94), and (3.97) for ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$ using Newton's method.Footnote 9 Once
$x$ using Newton's method.Footnote 9 Once ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$ are determined,
$x$ are determined, ![]() $\dot {M}$,
$\dot {M}$, ![]() $\chi _\textrm {H}$,
$\chi _\textrm {H}$, ![]() $\rho _\textrm {b}$,
$\rho _\textrm {b}$, ![]() $v_\textrm {Ab}$,
$v_\textrm {Ab}$, ![]() $q_\textrm {b}$,
$q_\textrm {b}$, ![]() $r_\textrm {c}$,
$r_\textrm {c}$, ![]() $r_\textrm {A}$, and
$r_\textrm {A}$, and ![]() $U_{\infty }$ are computed from (3.13), (3.45), (3.57), (3.63), (3.82), (3.88), (A 3), and (A 13), respectively. The approximate analytic solutions are derived in Appendix B.
$U_{\infty }$ are computed from (3.13), (3.45), (3.57), (3.63), (3.82), (3.88), (A 3), and (A 13), respectively. The approximate analytic solutions are derived in Appendix B.
4.1. Magnetic-field model
The equations in § 3 are compatible with any model for the radial profile of the magnetic-field strength, or, equivalently, any choice of ![]() $\eta (r)$. On the other hand, the approximate analytic solutions derived in Appendix B assume that
$\eta (r)$. On the other hand, the approximate analytic solutions derived in Appendix B assume that
To maintain consistency between the numerical and analytic solutions, and to avoid introducing additional complexity and free parameters, I take (4.1) to hold when computing the numerical solutions presented in this section. In essence, (4.1) amounts to assuming that all of the super-radial expansion of the magnetic field occurs inside the wave-modified sonic critical point. In measurements from the FIELDS experiment on the Parker Solar Probe (PSP) (Bale et al. Reference Bale, Goetz, Harvey, Turin, Bonnell, Dudok de Wit, Ergun, MacDowall, Pulupa and Andre2016) during PSP's first few orbits, ![]() $|B_r| \simeq 2.2 \mbox { nT} (1 \mbox { a.u.}/r)^2$ (Sam Badman, private communication), where a.u. is the abbreviation for astronomical unit. In order to match this
$|B_r| \simeq 2.2 \mbox { nT} (1 \mbox { a.u.}/r)^2$ (Sam Badman, private communication), where a.u. is the abbreviation for astronomical unit. In order to match this ![]() $B_r$ profile, I set
$B_r$ profile, I set
when computing the results shown in figures 3 through 6.

Figure 3. The outflow velocity ![]() $U$, density
$U$, density ![]() $\rho$, r.m.s. amplitude of the velocity fluctuation
$\rho$, r.m.s. amplitude of the velocity fluctuation ![]() $\delta v$, and temperature
$\delta v$, and temperature ![]() $T$ as functions of heliocentric distance
$T$ as functions of heliocentric distance ![]() $r$ in a numerical solution to the model equations with
$r$ in a numerical solution to the model equations with ![]() $\eta _\textrm {b} = 100$,
$\eta _\textrm {b} = 100$, ![]() $\sigma = 0.5$, and the parameter values in (4.1), (4.2), (4.6), and (4.7). The dotted lines in the top-left panel are described in the text. In the top panels and the lower-right panel, the circles are measurements from a 1 h interval containing PSP's first perihelion on 6 November 2018, from figure 1 of Kasper et al. (Reference Kasper, Bale, Belcher, Berthomier, Case, Chandran, Curtis, Gallagher, Gary and Golub2019). The error bars around the PSP data points in these three panels indicate the approximate range of values with a relative occurrence rate of at least 50 % of the peak occurrence rate within that 1 h interval. In the top-right panel, the error bars lie within the data point. In the lower-left panel, the PSP data point is from Chen et al. (Reference Chen, Bale, Bonnell, Borovikov, Bowen, Burgess, Case, Chandran, de Wit and Goetz2020), and the error bars around that data point show the approximate range of measured values near
$\sigma = 0.5$, and the parameter values in (4.1), (4.2), (4.6), and (4.7). The dotted lines in the top-left panel are described in the text. In the top panels and the lower-right panel, the circles are measurements from a 1 h interval containing PSP's first perihelion on 6 November 2018, from figure 1 of Kasper et al. (Reference Kasper, Bale, Belcher, Berthomier, Case, Chandran, Curtis, Gallagher, Gary and Golub2019). The error bars around the PSP data points in these three panels indicate the approximate range of values with a relative occurrence rate of at least 50 % of the peak occurrence rate within that 1 h interval. In the top-right panel, the error bars lie within the data point. In the lower-left panel, the PSP data point is from Chen et al. (Reference Chen, Bale, Bonnell, Borovikov, Bowen, Burgess, Case, Chandran, de Wit and Goetz2020), and the error bars around that data point show the approximate range of measured values near ![]() $r=35.7 R_{\odot }$ in figure 7 of Chen et al. (Reference Chen, Bale, Bonnell, Borovikov, Bowen, Burgess, Case, Chandran, de Wit and Goetz2020). The triangle in the lower-left panel is the value obtained by De Pontieu et al. (Reference De Pontieu, McIntosh, Carlsson, Hansteen, Tarbell, Schrijver, Title, Shine, Tsuneta and Katsukawa2007) from an analysis of the motion of filamentary structures in the low solar atmosphere based on observations from the Solar Optical Telescope on the Hinode satellite.
$r=35.7 R_{\odot }$ in figure 7 of Chen et al. (Reference Chen, Bale, Bonnell, Borovikov, Bowen, Burgess, Case, Chandran, de Wit and Goetz2020). The triangle in the lower-left panel is the value obtained by De Pontieu et al. (Reference De Pontieu, McIntosh, Carlsson, Hansteen, Tarbell, Schrijver, Title, Shine, Tsuneta and Katsukawa2007) from an analysis of the motion of filamentary structures in the low solar atmosphere based on observations from the Solar Optical Telescope on the Hinode satellite.

Figure 4. Mass outflow rate as a function of the effective fluctuating velocity at the photosphere ![]() $\delta v_{\odot \textrm {eff}} = f_\textrm {chr}^{1/2} \delta v_\odot$ (see (3.49)) for the parameter values in (4.1), (4.2), (4.7),
$\delta v_{\odot \textrm {eff}} = f_\textrm {chr}^{1/2} \delta v_\odot$ (see (3.49)) for the parameter values in (4.1), (4.2), (4.7), ![]() $\eta _\textrm {b} = 30$, and
$\eta _\textrm {b} = 30$, and ![]() $\sigma =0.18$, where
$\sigma =0.18$, where ![]() $f_\textrm {chr}$ is the chromospheric/transition-region AW transmission coefficient in (3.46). The corresponding r.m.s. photospheric velocity
$f_\textrm {chr}$ is the chromospheric/transition-region AW transmission coefficient in (3.46). The corresponding r.m.s. photospheric velocity ![]() $\delta v_\odot$ is shown at the top of the plot for the case in which
$\delta v_\odot$ is shown at the top of the plot for the case in which ![]() $f_\textrm {chr} = 0.05.$ The solid line plots (3.99) using the numerical solution to (3.67), (3.94), and (3.97). The dotted and short-dashed lines plot the approximate analytic results from (3.101) and (3.103), respectively. The vertical dash-dot line corresponds to
$f_\textrm {chr} = 0.05.$ The solid line plots (3.99) using the numerical solution to (3.67), (3.94), and (3.97). The dotted and short-dashed lines plot the approximate analytic results from (3.101) and (3.103), respectively. The vertical dash-dot line corresponds to ![]() $\epsilon _{\odot \textrm {cond}}$ in (B 14). The left and right edges of the shaded region correspond to
$\epsilon _{\odot \textrm {cond}}$ in (B 14). The left and right edges of the shaded region correspond to ![]() $\epsilon _{\odot \textrm {exp}, \textrm {min}}$ and
$\epsilon _{\odot \textrm {exp}, \textrm {min}}$ and ![]() $\epsilon _{\odot \textrm {exp}, \textrm {max}}$ in (B 35) and (B 36), respectively. To the right of the vertical long-dashed line,
$\epsilon _{\odot \textrm {exp}, \textrm {max}}$ in (B 35) and (B 36), respectively. To the right of the vertical long-dashed line, ![]() $r_\textrm {c} > r_\textrm {A}$, which violates (3.90) and the assumptions of the model.
$r_\textrm {c} > r_\textrm {A}$, which violates (3.90) and the assumptions of the model.

Figure 5. The dependence of various flow properties on the Wang-Sheeley super-radial expansion factor ![]() $f_{\textrm {max}, \textrm {WS}}$ (4.8) for the parameter values in (4.1), (4.2), and (4.6)–(4.9). All quantities are evaluated using numerical solutions to the model equations, with the exception of
$f_{\textrm {max}, \textrm {WS}}$ (4.8) for the parameter values in (4.1), (4.2), and (4.6)–(4.9). All quantities are evaluated using numerical solutions to the model equations, with the exception of ![]() $\dot {M}_2^\textrm {(exp)}$,
$\dot {M}_2^\textrm {(exp)}$, ![]() $\dot {M}_4^\textrm {(exp)}$,
$\dot {M}_4^\textrm {(exp)}$, ![]() $U_{\infty , 2}^\textrm {(exp)}$, and
$U_{\infty , 2}^\textrm {(exp)}$, and ![]() $U_{\infty , 4}^\textrm {(exp)}$, which are defined in (B 32) and (B 33), and the data points labeled ‘WS empirical’, which are taken from table 2 of Wang & Sheeley (Reference Wang and Sheeley1990). The horizontal error bars on these data points convey the half widths of the
$U_{\infty , 4}^\textrm {(exp)}$, which are defined in (B 32) and (B 33), and the data points labeled ‘WS empirical’, which are taken from table 2 of Wang & Sheeley (Reference Wang and Sheeley1990). The horizontal error bars on these data points convey the half widths of the ![]() $f_{\textrm {max}, \textrm {WS}}$ data bins in that table. The vertical error bars correspond to one-half of the
$f_{\textrm {max}, \textrm {WS}}$ data bins in that table. The vertical error bars correspond to one-half of the ![]() $100 \mbox { km} \mbox { s}^{-1}$ increment between the discretised
$100 \mbox { km} \mbox { s}^{-1}$ increment between the discretised ![]() $U_{\infty }$ values that define four of the five data bins. The quantity
$U_{\infty }$ values that define four of the five data bins. The quantity ![]() $I_1 \rho _\textrm {b} \overline {c_\textrm {s}}^3$ in the left panel of the second row is the low-Mach-number approximation to
$I_1 \rho _\textrm {b} \overline {c_\textrm {s}}^3$ in the left panel of the second row is the low-Mach-number approximation to ![]() $q_\textrm {b}$ given in (3.83).
$q_\textrm {b}$ given in (3.83).
4.2. Values of the AW power at the coronal base and  $\delta v_{\odot {\rm eff}}$
$\delta v_{\odot {\rm eff}}$
Equations (3.46) and (3.49) and the flux-conservation relation ![]() $A_\textrm {b} B_\textrm {b} = A_{\odot } B_{\odot }$ imply that
$A_\textrm {b} B_\textrm {b} = A_{\odot } B_{\odot }$ imply that
 \begin{equation} \delta v_{{\odot} \textrm{eff}} = \left(\frac{4{\rm \pi}}{\rho_{{\odot}}}\right)^{1/4} \left( \frac{P_\textrm{AWb}}{B_\textrm{b} A_\textrm{b}} \right)^{1/2}. \end{equation}
\begin{equation} \delta v_{{\odot} \textrm{eff}} = \left(\frac{4{\rm \pi}}{\rho_{{\odot}}}\right)^{1/4} \left( \frac{P_\textrm{AWb}}{B_\textrm{b} A_\textrm{b}} \right)^{1/2}. \end{equation}
When the solar wind is powered primarily by AWs, ![]() $P_\textrm {AWb}$ is approximately equal to the value of
$P_\textrm {AWb}$ is approximately equal to the value of ![]() $\dot {E}_\textrm {m0}$ in (1.3), i.e.,
$\dot {E}_\textrm {m0}$ in (1.3), i.e.,
Upon evaluating the right-hand side of (4.4) using the data in table 1 of Schwadron & McComas (Reference Schwadron and McComas2008) for Ulysses’ third northern polar pass (3NPP), one obtains
which corresponds to ![]() $P_\textrm {AWb} / (4 {\rm \pi}R_{\odot }^2) = 0.59 \times 10^5 \mbox { erg} \mbox { cm}^{-2} \mbox { s}^{-1}$. I use the 3NPP data because this is the part of Ulysses's first three orbits during which the average scaled radial magnetic field
$P_\textrm {AWb} / (4 {\rm \pi}R_{\odot }^2) = 0.59 \times 10^5 \mbox { erg} \mbox { cm}^{-2} \mbox { s}^{-1}$. I use the 3NPP data because this is the part of Ulysses's first three orbits during which the average scaled radial magnetic field ![]() $|\langle B_r \rangle | \cdot (r/ 1 \mbox { a.u.})^2$ was most consistent with (4.2) (in the 3NPP data,
$|\langle B_r \rangle | \cdot (r/ 1 \mbox { a.u.})^2$ was most consistent with (4.2) (in the 3NPP data, ![]() $|\langle B_r \rangle | \cdot (r/ 1 \mbox { a.u.})^2 = 2.1 \pm 0.08 \mbox { nT}$), and because
$|\langle B_r \rangle | \cdot (r/ 1 \mbox { a.u.})^2 = 2.1 \pm 0.08 \mbox { nT}$), and because ![]() $\dot {M}$ is strongly correlated with the average scaled radial magnetic field (Schwadron & McComas Reference Schwadron and McComas2008). Equations (3.47), (4.2), (4.3), and (4.5) and the relation
$\dot {M}$ is strongly correlated with the average scaled radial magnetic field (Schwadron & McComas Reference Schwadron and McComas2008). Equations (3.47), (4.2), (4.3), and (4.5) and the relation ![]() $B_\textrm {b} A_\textrm {b} = |B_r(1 \mbox { a.u.})| 4 {\rm \pi}(1 \mbox { a.u.})^2$ imply that
$B_\textrm {b} A_\textrm {b} = |B_r(1 \mbox { a.u.})| 4 {\rm \pi}(1 \mbox { a.u.})^2$ imply that
This value of ![]() $\delta v_{\odot \textrm {eff}}$ is used in figures 3, 5, and 7.
$\delta v_{\odot \textrm {eff}}$ is used in figures 3, 5, and 7.

Figure 7. The dependence of various flow properties on the Wang-Sheeley super-radial expansion factor ![]() $f_{\textrm {max},\textrm {WS}}$ (4.8) and the strength of the radial magnetic field at
$f_{\textrm {max},\textrm {WS}}$ (4.8) and the strength of the radial magnetic field at ![]() $r= 1 \mbox { a.u.}$
$r= 1 \mbox { a.u.}$
4.3. Free parameters
As discussed in § 3.8, there are two free parameters in the model: ![]() $l_\textrm {b}$ (the AW dissipation length scale at
$l_\textrm {b}$ (the AW dissipation length scale at ![]() $r_\textrm {b}$) and
$r_\textrm {b}$) and ![]() $\sigma$ (the dimensionless coefficient in the turbulent heating rate). The solutions to (3.67), (3.94), and (3.97) are not very sensitive to the value of
$\sigma$ (the dimensionless coefficient in the turbulent heating rate). The solutions to (3.67), (3.94), and (3.97) are not very sensitive to the value of ![]() $l_\textrm {b}$. Throughout the rest of this section,
$l_\textrm {b}$. Throughout the rest of this section, ![]() $l_\textrm {b}$ is thus simply fixed at a value that seems physically reasonable:
$l_\textrm {b}$ is thus simply fixed at a value that seems physically reasonable:
On the other hand, the solutions depend sensitively on the value of ![]() $\sigma$. Larger values of
$\sigma$. Larger values of ![]() $\sigma$ cause a larger fraction of the AW power at the coronal base
$\sigma$ cause a larger fraction of the AW power at the coronal base ![]() $P_\textrm {AWb}$ to be dissipated in the quasi-isothermal sub-Alfvénic region, which increases
$P_\textrm {AWb}$ to be dissipated in the quasi-isothermal sub-Alfvénic region, which increases ![]() $\dot {M}$ (see, e.g. (2.15) and (2.16)). For fixed
$\dot {M}$ (see, e.g. (2.15) and (2.16)). For fixed ![]() $P_\textrm {AWb}$, increasing
$P_\textrm {AWb}$, increasing ![]() $\dot {M}$ decreases
$\dot {M}$ decreases ![]() $U_{\infty }$. In some of the examples to follow,
$U_{\infty }$. In some of the examples to follow, ![]() $\sigma$ is varied to optimise agreement between the model and observations, as described further in §§ 4.4 and 4.6. The super-radial expansion factor at the coronal base,
$\sigma$ is varied to optimise agreement between the model and observations, as described further in §§ 4.4 and 4.6. The super-radial expansion factor at the coronal base, ![]() $\eta _\textrm {b}$, also varies in the model, but this quantity is in principle observable for individual flux tubes. The value of
$\eta _\textrm {b}$, also varies in the model, but this quantity is in principle observable for individual flux tubes. The value of ![]() $\eta _\textrm {b}$ is thus treated as an input into the model rather than an adjustable parameter.
$\eta _\textrm {b}$ is thus treated as an input into the model rather than an adjustable parameter.
4.4. Fiducial solution matching measurements from Parker Solar Probe's first perihelion
Figure 3 illustrates the ![]() $r$ dependence of the outflow velocity, density, fluctuating velocity, and temperature in a numerical solution to the model equations that is designed to agree with measurements from PSP's first perihelion encounter (E1) on 6 November 2018. The procedure for computing
$r$ dependence of the outflow velocity, density, fluctuating velocity, and temperature in a numerical solution to the model equations that is designed to agree with measurements from PSP's first perihelion encounter (E1) on 6 November 2018. The procedure for computing ![]() $U(r)$ and
$U(r)$ and ![]() $T(r)$ is described in Appendix A. In order to solve for
$T(r)$ is described in Appendix A. In order to solve for ![]() $U$ at some radius
$U$ at some radius ![]() $r$, the value of
$r$, the value of ![]() $\eta$ must be specified at that
$\eta$ must be specified at that ![]() $r$. For figure 3, I set
$r$. For figure 3, I set ![]() $\eta (r) = 1 + (\eta _\textrm {b} - 1) \exp (-(r-r_\textrm {b})^2/(0.02 R_{\odot } )^2)$, which is effectively unity at
$\eta (r) = 1 + (\eta _\textrm {b} - 1) \exp (-(r-r_\textrm {b})^2/(0.02 R_{\odot } )^2)$, which is effectively unity at ![]() $r= r_\textrm {c}$, consistent with (4.1). This choice of
$r= r_\textrm {c}$, consistent with (4.1). This choice of ![]() $\eta (r)$ is not realistic for the low corona (see, e.g. Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007), but the flow profile in the low corona is not a focus of this work. It should be noted that while the value of
$\eta (r)$ is not realistic for the low corona (see, e.g. Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007), but the flow profile in the low corona is not a focus of this work. It should be noted that while the value of ![]() $\delta v$ at
$\delta v$ at ![]() $r=r_\textrm {b}$ (i.e.
$r=r_\textrm {b}$ (i.e. ![]() $\delta v_\textrm {b}$) shown in the lower-left panel of figure 3 depends on
$\delta v_\textrm {b}$) shown in the lower-left panel of figure 3 depends on ![]() $\eta _\textrm {b}$ through (3.48), (3.57), and (3.62),
$\eta _\textrm {b}$ through (3.48), (3.57), and (3.62), ![]() $\delta v_\textrm {b}$ does not on the way in which
$\delta v_\textrm {b}$ does not on the way in which ![]() $\eta (r)$ decreases from
$\eta (r)$ decreases from ![]() $\eta _\textrm {b }$ to 1.
$\eta _\textrm {b }$ to 1.
The solution in figure 3 is based upon the somewhat arbitrary assumption that ![]() $\eta _\textrm {b} = 100$ in the magnetic flux tube encountered by PSP at the time of its first perihelion. The value of
$\eta _\textrm {b} = 100$ in the magnetic flux tube encountered by PSP at the time of its first perihelion. The value of ![]() $\sigma$ is set equal to 0.5 to optimise the agreement between the model and the data. Fits of comparable (in some cases superior) quality can be obtained for different values of
$\sigma$ is set equal to 0.5 to optimise the agreement between the model and the data. Fits of comparable (in some cases superior) quality can be obtained for different values of ![]() $\eta _\textrm {b}$. For example, the parameter combinations
$\eta _\textrm {b}$. For example, the parameter combinations ![]() $(\eta _\textrm {b}, \sigma ) = (300, 0.47)$ and
$(\eta _\textrm {b}, \sigma ) = (300, 0.47)$ and ![]() $(\eta _\textrm {b}, \sigma ) = (30,0.55)$ lead to similar agreement with the data. Modelling of the solar magnetic field during PSP E1 suggests that the solar-wind stream encountered by PSP at the time of PSP's first perihelion originated in a small equatorial coronal hole (Bale et al. Reference Bale, Badman, Bonnell, Bowen, Burgess, Case, Cattell, Chandran, Chaston and Chen2019). The fact that all four quantities plotted in figure 3 can be matched by varying the single parameter
$(\eta _\textrm {b}, \sigma ) = (30,0.55)$ lead to similar agreement with the data. Modelling of the solar magnetic field during PSP E1 suggests that the solar-wind stream encountered by PSP at the time of PSP's first perihelion originated in a small equatorial coronal hole (Bale et al. Reference Bale, Badman, Bonnell, Bowen, Burgess, Case, Cattell, Chandran, Chaston and Chen2019). The fact that all four quantities plotted in figure 3 can be matched by varying the single parameter ![]() $\sigma$ suggests that the model is reasonably successful at capturing the physical processes that control the heating and acceleration of coronal-hole outflows.
$\sigma$ suggests that the model is reasonably successful at capturing the physical processes that control the heating and acceleration of coronal-hole outflows.
The dotted lines in the top-left panel of figure 3 are solutions of the Bernoulli equation (3.95) for different values of the Bernoulli constant ![]() $\varGamma$. One of the dotted lines intersects the solid line, and that intersection occurs at the wave-modified sonic critical point,
$\varGamma$. One of the dotted lines intersects the solid line, and that intersection occurs at the wave-modified sonic critical point, ![]() $r=r_\textrm {c}$. That dotted line is an accretion-like solution of (3.95) with the same value of
$r=r_\textrm {c}$. That dotted line is an accretion-like solution of (3.95) with the same value of ![]() $\varGamma$ as in the model solution but with
$\varGamma$ as in the model solution but with ![]() $\textrm {d} U / \textrm {d} r < 0$ at
$\textrm {d} U / \textrm {d} r < 0$ at ![]() $r=r_\textrm {c}$.
$r=r_\textrm {c}$.
4.5. Illustration of the conduction-dominated and expansion-dominated regimes
Figure 4 plots ![]() $\dot {M}$ as a function of
$\dot {M}$ as a function of ![]() $\delta v_{\odot \textrm {eff}}$ when
$\delta v_{\odot \textrm {eff}}$ when ![]() $\eta _\textrm {b} = 30$ and
$\eta _\textrm {b} = 30$ and ![]() $\sigma = 0.18$. This figure includes the numerical solution to (3.67), (3.94), and (3.97) as well as the approximate analytic results
$\sigma = 0.18$. This figure includes the numerical solution to (3.67), (3.94), and (3.97) as well as the approximate analytic results ![]() $\dot {M}^\textrm {(cond)}$ and
$\dot {M}^\textrm {(cond)}$ and ![]() $\dot {M}^\textrm {(exp)}_0$ from (3.101) and (3.103). The vertical dash-dot line in this figure corresponds to
$\dot {M}^\textrm {(exp)}_0$ from (3.101) and (3.103). The vertical dash-dot line in this figure corresponds to ![]() $\epsilon _{\odot \textrm {cond}}$ in (B 14). The conduction-dominated approximation that gives rise to
$\epsilon _{\odot \textrm {cond}}$ in (B 14). The conduction-dominated approximation that gives rise to ![]() $\dot {M}^\textrm {(cond)}$ in (3.101) assumes that
$\dot {M}^\textrm {(cond)}$ in (3.101) assumes that ![]() $\epsilon _\odot \ll \epsilon _{\odot \textrm {cond}}$.Footnote 10 The shaded region corresponds to
$\epsilon _\odot \ll \epsilon _{\odot \textrm {cond}}$.Footnote 10 The shaded region corresponds to ![]() $\epsilon _{\odot \textrm {exp}, \textrm {min}}< \epsilon _\odot < \epsilon _{\odot \textrm {exp}, \textrm {max}}$, where
$\epsilon _{\odot \textrm {exp}, \textrm {min}}< \epsilon _\odot < \epsilon _{\odot \textrm {exp}, \textrm {max}}$, where ![]() $\epsilon _{\odot \textrm {exp}, \textrm {min}}$ and
$\epsilon _{\odot \textrm {exp}, \textrm {min}}$ and ![]() $\epsilon _{\odot \textrm {exp}, \textrm {max}}$ are defined in (B 35) and (B 36). The expansion-dominated approximation in § B.2 assumes that
$\epsilon _{\odot \textrm {exp}, \textrm {max}}$ are defined in (B 35) and (B 36). The expansion-dominated approximation in § B.2 assumes that ![]() $\epsilon _{\odot \textrm {exp}, \textrm {min}}\ll \epsilon _\odot \ll \epsilon _{\odot \textrm {exp}, \textrm {max}}$. The vertical long-dashed line corresponds to the condition
$\epsilon _{\odot \textrm {exp}, \textrm {min}}\ll \epsilon _\odot \ll \epsilon _{\odot \textrm {exp}, \textrm {max}}$. The vertical long-dashed line corresponds to the condition ![]() $r_\textrm {c} = r_\textrm {A}$. To the right of this line,
$r_\textrm {c} = r_\textrm {A}$. To the right of this line, ![]() $\dot {M}$ and the solar-wind density become so large that
$\dot {M}$ and the solar-wind density become so large that ![]() $r_\textrm {A} < r_\textrm {c}$, violating (3.90) and the assumptions underlying the model. In conjunction with (4.6), figure 4 illustrates that the expansion-dominated regime is relevant to the solar wind and that the conduction-dominated regime corresponds to values of
$r_\textrm {A} < r_\textrm {c}$, violating (3.90) and the assumptions underlying the model. In conjunction with (4.6), figure 4 illustrates that the expansion-dominated regime is relevant to the solar wind and that the conduction-dominated regime corresponds to values of ![]() $\delta v_{\odot \textrm {eff}}$ much smaller than the solar value.
$\delta v_{\odot \textrm {eff}}$ much smaller than the solar value.
4.6. Anti-correlation between the coronal super-radial expansion factor and  $U_{\infty }$
$U_{\infty }$
Wang & Sheeley (Reference Wang and Sheeley1990) showed that the outflow velocity in a solar-wind stream at ![]() $r=1 {\rm a.u.}$ is anti-correlated with the super-radial expansion factor in the coronal magnetic flux tube from which the solar-wind stream originated. To compare their results with the model developed in § 3, I follow Cranmer et al. (Reference Cranmer, van Ballegooijen and Edgar2007) by defining the Wang & Sheeley (Reference Wang and Sheeley1990) coronal super-radial expansion factor
$r=1 {\rm a.u.}$ is anti-correlated with the super-radial expansion factor in the coronal magnetic flux tube from which the solar-wind stream originated. To compare their results with the model developed in § 3, I follow Cranmer et al. (Reference Cranmer, van Ballegooijen and Edgar2007) by defining the Wang & Sheeley (Reference Wang and Sheeley1990) coronal super-radial expansion factor ![]() $f_{\textrm {max}, \textrm {WS}}$ to be
$f_{\textrm {max}, \textrm {WS}}$ to be ![]() $\eta (1.04 R_{\odot })/ \eta (2.5 R_{\odot })$. I then compute
$\eta (1.04 R_{\odot })/ \eta (2.5 R_{\odot })$. I then compute ![]() $\eta (1.04 R_{\odot })$ and
$\eta (1.04 R_{\odot })$ and ![]() $\eta (2.5 R_{\odot })$ using a magnetic-field model similar to that used by Cranmer et al. (Reference Cranmer, van Ballegooijen and Edgar2007). In particular, I employ the global solar-magnetic-field model of Banaszkiewicz, Axford & McKenzie (Reference Banaszkiewicz, Axford and McKenzie1998) with the parameter values listed below their equation (2) (
$\eta (2.5 R_{\odot })$ using a magnetic-field model similar to that used by Cranmer et al. (Reference Cranmer, van Ballegooijen and Edgar2007). In particular, I employ the global solar-magnetic-field model of Banaszkiewicz, Axford & McKenzie (Reference Banaszkiewicz, Axford and McKenzie1998) with the parameter values listed below their equation (2) (![]() $K=1$,
$K=1$, ![]() $M=1.789$,
$M=1.789$, ![]() $a_1^\textrm {(B98)} = 1.538$, and
$a_1^\textrm {(B98)} = 1.538$, and ![]() $Q=1.5$). I supplement this global magnetic field with the low-solar-atmosphere magnetic-field model of Hackenberg et al. (Reference Hackenberg, Marsch and Mann2000) using the same parameter values listed in their figure 1 (
$Q=1.5$). I supplement this global magnetic field with the low-solar-atmosphere magnetic-field model of Hackenberg et al. (Reference Hackenberg, Marsch and Mann2000) using the same parameter values listed in their figure 1 (![]() $L = 30 \mbox { Mm}$,
$L = 30 \mbox { Mm}$, ![]() $d = 0.34 \mbox { Mm}$,
$d = 0.34 \mbox { Mm}$, ![]() $B_0 = 11.8 \mbox { G}$, and
$B_0 = 11.8 \mbox { G}$, and ![]() $B_\textrm {max} = 1.5 \mbox { kG}$). I then integrate out along a magnetic-field line at the edge of the polar corona hole in the Banaszkiewicz et al. (Reference Banaszkiewicz, Axford and McKenzie1998) model, compute
$B_\textrm {max} = 1.5 \mbox { kG}$). I then integrate out along a magnetic-field line at the edge of the polar corona hole in the Banaszkiewicz et al. (Reference Banaszkiewicz, Axford and McKenzie1998) model, compute ![]() $\eta (r)$, and obtain
$\eta (r)$, and obtain
I take (4.8) to hold even as ![]() $\eta _\textrm {b}$ is varied in figures 5, 6, and 7. This is equivalent to assuming that if local magnetic structures on the Sun cause
$\eta _\textrm {b}$ is varied in figures 5, 6, and 7. This is equivalent to assuming that if local magnetic structures on the Sun cause ![]() $\eta _\textrm {b}$ to increase or decrease by some factor relative to the Hackenberg/Banaszkiewicz model just described, then
$\eta _\textrm {b}$ to increase or decrease by some factor relative to the Hackenberg/Banaszkiewicz model just described, then ![]() $\eta (1.04 R_{\odot })$ increases or decreases by the same factor, but
$\eta (1.04 R_{\odot })$ increases or decreases by the same factor, but ![]() $\eta (2.5 R_{\odot })$ does not change.
$\eta (2.5 R_{\odot })$ does not change.
If ![]() $\sigma$ is fixed while
$\sigma$ is fixed while ![]() $\eta _\textrm {b}$ is varied, the model of § 3 does not agree with results of Wang & Sheeley (Reference Wang and Sheeley1990) shown in the top-right panel of figure 5. On the other hand, the model becomes consistent with those results if
$\eta _\textrm {b}$ is varied, the model of § 3 does not agree with results of Wang & Sheeley (Reference Wang and Sheeley1990) shown in the top-right panel of figure 5. On the other hand, the model becomes consistent with those results if ![]() $\sigma$ is taken to have a power-law dependence on
$\sigma$ is taken to have a power-law dependence on ![]() $\eta _\textrm {b}$ of the form
$\eta _\textrm {b}$ of the form
Equation (4.9) is used to determine ![]() $\sigma$ in figures 5 through 7. The implication of (4.9) that
$\sigma$ in figures 5 through 7. The implication of (4.9) that ![]() $\sigma$ is an increasing function of
$\sigma$ is an increasing function of ![]() $\eta _\textrm {b}$ is plausible because increasing
$\eta _\textrm {b}$ is plausible because increasing ![]() $\eta _\textrm {b}$ increases
$\eta _\textrm {b}$ increases ![]() $v_\textrm {Ab}$, as can be seen from (3.63). This, in turn, increases the number of Alfvén-speed scale heights between the coronal base and the Alfvén critical point (
$v_\textrm {Ab}$, as can be seen from (3.63). This, in turn, increases the number of Alfvén-speed scale heights between the coronal base and the Alfvén critical point (![]() $\int _{r_\textrm {b}}^{r_\textrm {A}} (1/v_\textrm {A}) | \,\textrm {d} v_\textrm {A}/ \textrm {d} r|\, \textrm {d} r$), which increases the fraction of
$\int _{r_\textrm {b}}^{r_\textrm {A}} (1/v_\textrm {A}) | \,\textrm {d} v_\textrm {A}/ \textrm {d} r|\, \textrm {d} r$), which increases the fraction of ![]() $P_\textrm {AWb}$ that is dissipated at
$P_\textrm {AWb}$ that is dissipated at ![]() $r<r_\textrm {A}$ (Chandran & Hollweg Reference Chandran and Hollweg2009). Further work, however, is needed to clarify how the structure of the coronal magnetic field influences the rate of turbulent dissipation along different magnetic flux tubes with different values of
$r<r_\textrm {A}$ (Chandran & Hollweg Reference Chandran and Hollweg2009). Further work, however, is needed to clarify how the structure of the coronal magnetic field influences the rate of turbulent dissipation along different magnetic flux tubes with different values of ![]() $\eta _\textrm {b}$ and to test the extent to which (3.41) and (4.9) are consistent with more rigorous treatments of AW turbulence in the sub-Alfvénic region of the solar wind.
$\eta _\textrm {b}$ and to test the extent to which (3.41) and (4.9) are consistent with more rigorous treatments of AW turbulence in the sub-Alfvénic region of the solar wind.
The top-left panel of figure 5 shows that as ![]() $f_{\textrm {max}, \textrm {WS}}$ ranges from
$f_{\textrm {max}, \textrm {WS}}$ ranges from ![]() $\simeq 3$ to
$\simeq 3$ to ![]() $\simeq 30$,
$\simeq 30$, ![]() $\dot {M}$ varies from
$\dot {M}$ varies from ![]() $10^{-14} M_{\odot } \mbox { yr}^{-1}$ to
$10^{-14} M_{\odot } \mbox { yr}^{-1}$ to ![]() $2\times 10^{-14} M_{\odot } \mbox { yr}^{-1}$, values that are similar to the solar-mass-loss rates inferred from Ulysses and PSP measurements (McComas et al. Reference McComas, Barraclough, Funsten, Gosling, Santiago-Muñoz, Skoug, Goldstein, Neugebauer, Riley and Balogh2000; Schwadron & McComas Reference Schwadron and McComas2008; Kasper et al. Reference Kasper, Bale, Belcher, Berthomier, Case, Chandran, Curtis, Gallagher, Gary and Golub2019). The fourth-order analytic approximation
$2\times 10^{-14} M_{\odot } \mbox { yr}^{-1}$, values that are similar to the solar-mass-loss rates inferred from Ulysses and PSP measurements (McComas et al. Reference McComas, Barraclough, Funsten, Gosling, Santiago-Muñoz, Skoug, Goldstein, Neugebauer, Riley and Balogh2000; Schwadron & McComas Reference Schwadron and McComas2008; Kasper et al. Reference Kasper, Bale, Belcher, Berthomier, Case, Chandran, Curtis, Gallagher, Gary and Golub2019). The fourth-order analytic approximation ![]() $\dot {M}_4^\textrm {(exp)}$ from (B 32) reproduces the numerical solution to the model equations reasonably well. The second-order analytic approximation
$\dot {M}_4^\textrm {(exp)}$ from (B 32) reproduces the numerical solution to the model equations reasonably well. The second-order analytic approximation ![]() $\dot {M}_2^\textrm {(exp)}$ is also reasonably accurate at
$\dot {M}_2^\textrm {(exp)}$ is also reasonably accurate at ![]() $f_{\textrm {max}, \textrm {WS}} >rsim 3$, but deviates markedly from the numerical solution at
$f_{\textrm {max}, \textrm {WS}} >rsim 3$, but deviates markedly from the numerical solution at ![]() $f_{\textrm {max}, \textrm {WS}} \lesssim 2$. A similar comment applies to the top-right panel of figure 5, which also shows that the model agrees fairly well with observational constraints on
$f_{\textrm {max}, \textrm {WS}} \lesssim 2$. A similar comment applies to the top-right panel of figure 5, which also shows that the model agrees fairly well with observational constraints on ![]() $U_{\infty }(f_{\textrm {max}, \textrm {WS}})$ when (4.9) holds. The left panel of the second row of figure 5 shows that the low-Mach-number approximation to
$U_{\infty }(f_{\textrm {max}, \textrm {WS}})$ when (4.9) holds. The left panel of the second row of figure 5 shows that the low-Mach-number approximation to ![]() $q_\textrm {b}$ given in (3.83) is quite accurate at small
$q_\textrm {b}$ given in (3.83) is quite accurate at small ![]() $f_{\textrm {max}, \textrm {WS}}$, where
$f_{\textrm {max}, \textrm {WS}}$, where ![]() $U_\textrm {b}/ \overline {c_\textrm {s}} \ll 1$ (see the right panel in the second row of this figure). However, as
$U_\textrm {b}/ \overline {c_\textrm {s}} \ll 1$ (see the right panel in the second row of this figure). However, as ![]() $f_{\textrm {max}, \textrm {WS}}$ increases,
$f_{\textrm {max}, \textrm {WS}}$ increases, ![]() $U_\textrm {b}$ increases, because the outflow is concentrated into a smaller cross-sectional area at the coronal base. This increase in
$U_\textrm {b}$ increases, because the outflow is concentrated into a smaller cross-sectional area at the coronal base. This increase in ![]() $U_\textrm {b}$ leads to larger losses of internal energy within the transition region from
$U_\textrm {b}$ leads to larger losses of internal energy within the transition region from ![]() $p\,\textrm {d} V$ work and advection, which, in turn, causes
$p\,\textrm {d} V$ work and advection, which, in turn, causes ![]() $q_\textrm {b}$ to increase above the low-Mach-number scaling so that conductive heating within the transition region can balance the additional non-radiative cooling. This same panel also shows that
$q_\textrm {b}$ to increase above the low-Mach-number scaling so that conductive heating within the transition region can balance the additional non-radiative cooling. This same panel also shows that ![]() $q_\textrm {b}$ is significantly smaller than the AW energy flux at the coronal base (
$q_\textrm {b}$ is significantly smaller than the AW energy flux at the coronal base (![]() $\simeq \rho _\textrm {b} (\delta v_\textrm {b})^2 v_\textrm {Ab} = \rho _{\odot }^{1/2} (\delta v_{\odot \textrm {eff}})^2 B_\textrm {b} /\sqrt {4{\rm \pi} }$), which increases with
$\simeq \rho _\textrm {b} (\delta v_\textrm {b})^2 v_\textrm {Ab} = \rho _{\odot }^{1/2} (\delta v_{\odot \textrm {eff}})^2 B_\textrm {b} /\sqrt {4{\rm \pi} }$), which increases with ![]() $f_{\textrm {max}, \textrm {WS}}$ because increasing
$f_{\textrm {max}, \textrm {WS}}$ because increasing ![]() $f_{\textrm {max}, \textrm {WS}}$ increases
$f_{\textrm {max}, \textrm {WS}}$ increases ![]() $\eta _\textrm {b}$ and hence
$\eta _\textrm {b}$ and hence ![]() $B_\textrm {b}$. The lower-left panel of figure 5 shows that
$B_\textrm {b}$. The lower-left panel of figure 5 shows that ![]() $\rho _\textrm {b}$ increases by a factor of
$\rho _\textrm {b}$ increases by a factor of ![]() $\simeq 10$ as
$\simeq 10$ as ![]() $f_{\textrm {max}, \textrm {WS}}$ increases from 1 to 100, consistent with the
$f_{\textrm {max}, \textrm {WS}}$ increases from 1 to 100, consistent with the ![]() $\rho _\textrm {b} \propto \eta _\textrm {b}^{1/2} x^{1/4}$ scaling in (3.57) and (3.62), given that
$\rho _\textrm {b} \propto \eta _\textrm {b}^{1/2} x^{1/4}$ scaling in (3.57) and (3.62), given that ![]() $x = \overline {c_\textrm {s}}^2/v_\textrm {esc}^2$ is approximately constant over this range of
$x = \overline {c_\textrm {s}}^2/v_\textrm {esc}^2$ is approximately constant over this range of ![]() $f_\textrm {max}$. The lower-right panel shows that
$f_\textrm {max}$. The lower-right panel shows that ![]() $r_\textrm {c}$ is typically several solar radii, whereas
$r_\textrm {c}$ is typically several solar radii, whereas ![]() $r_\textrm {A}$ ranges from
$r_\textrm {A}$ ranges from ![]() $12 R_{\odot }$ to
$12 R_{\odot }$ to ![]() $15 R_{\odot }$ for this set of parameters.
$15 R_{\odot }$ for this set of parameters.
4.7. Dependence of the flow properties on the AW power, super-radial expansion factor, and strength of the interplanetary magnetic field
The contour plots in figure 6 show how several quantities vary as functions of ![]() $f_{\textrm {max}, \textrm {WS}}$ and
$f_{\textrm {max}, \textrm {WS}}$ and ![]() $\delta v_{\odot \textrm {eff}}$ in numerical solutions to the model equations based on the parameter values in (4.1), (4.2), (4.7), and (4.9). The top panels of figure 6 show that
$\delta v_{\odot \textrm {eff}}$ in numerical solutions to the model equations based on the parameter values in (4.1), (4.2), (4.7), and (4.9). The top panels of figure 6 show that ![]() $\dot {M}$ is an increasing function of both
$\dot {M}$ is an increasing function of both ![]() $f_{\textrm {max}, \textrm {WS}}$ and
$f_{\textrm {max}, \textrm {WS}}$ and ![]() $\delta v_{\odot \textrm {eff}}$, whereas
$\delta v_{\odot \textrm {eff}}$, whereas ![]() $U_\infty$ is a decreasing function of both
$U_\infty$ is a decreasing function of both ![]() $f_{\textrm {max}, \textrm {WS}}$ and
$f_{\textrm {max}, \textrm {WS}}$ and ![]() $\delta v_{\odot \textrm {eff}}$. The second row shows that
$\delta v_{\odot \textrm {eff}}$. The second row shows that ![]() $r_\textrm {A}$ is a strongly decreasing function of
$r_\textrm {A}$ is a strongly decreasing function of ![]() $\delta v_{\odot \textrm {eff}}$ and only weakly dependent on
$\delta v_{\odot \textrm {eff}}$ and only weakly dependent on ![]() $f_{\textrm {max}, \textrm {WS}}$ for values of
$f_{\textrm {max}, \textrm {WS}}$ for values of ![]() $\delta v_{\odot \textrm {eff}}$ comparable to the Sun-like value in (4.6). The right panel of this row shows that
$\delta v_{\odot \textrm {eff}}$ comparable to the Sun-like value in (4.6). The right panel of this row shows that ![]() $r_\textrm {c}$ is an increasing function of
$r_\textrm {c}$ is an increasing function of ![]() $f_{\textrm {max}, \textrm {WS}}$ and, for the most part, a decreasing function of
$f_{\textrm {max}, \textrm {WS}}$ and, for the most part, a decreasing function of ![]() $\delta v_{\odot \textrm {eff}}$. The lower-left panel of figure 6 shows that
$\delta v_{\odot \textrm {eff}}$. The lower-left panel of figure 6 shows that ![]() $\overline {c_\textrm {s}}$ varies only weakly with
$\overline {c_\textrm {s}}$ varies only weakly with ![]() $f_{\textrm {max}, \textrm {WS}}$ and
$f_{\textrm {max}, \textrm {WS}}$ and ![]() $\delta v_{\odot \textrm {eff}}$. As shown in the lower-right panel,
$\delta v_{\odot \textrm {eff}}$. As shown in the lower-right panel, ![]() $\chi _\textrm {H}$ varies by a factor of
$\chi _\textrm {H}$ varies by a factor of ![]() $\simeq 2$ over the parameter range shown. If
$\simeq 2$ over the parameter range shown. If ![]() $\delta v_{\odot \textrm {eff}}$ is set equal to the value in (4.6) and
$\delta v_{\odot \textrm {eff}}$ is set equal to the value in (4.6) and ![]() $f_\textrm {max}$ is restricted to the interval
$f_\textrm {max}$ is restricted to the interval ![]() $(2, 8)$ so that
$(2, 8)$ so that ![]() $U_{\infty }$ in the upper-right panel takes on fast-wind-like values of 600–800
$U_{\infty }$ in the upper-right panel takes on fast-wind-like values of 600–800 ![]() $\mbox { km} \mbox { s}^{-1}$, then
$\mbox { km} \mbox { s}^{-1}$, then ![]() $\chi _\textrm {H} \simeq 0.5 \text {--}0.7$, consistent with direct numerical simulations of reflection-driven AW turbulence (Perez et al. Reference Perez, Chandran, Klein and Martinovic2021).
$\chi _\textrm {H} \simeq 0.5 \text {--}0.7$, consistent with direct numerical simulations of reflection-driven AW turbulence (Perez et al. Reference Perez, Chandran, Klein and Martinovic2021).
Figure 7 displays contour plots of the same quantities as in figure 6, but this time as functions of ![]() $f_{\textrm {max}, \textrm {WS}}$ and
$f_{\textrm {max}, \textrm {WS}}$ and ![]() $B_\ast$, or, equivalently,
$B_\ast$, or, equivalently, ![]() $B_r(\mbox {1 a.u.})$, using the parameters in (4.1), (4.6), (4.7), and (4.9). The top panels show that
$B_r(\mbox {1 a.u.})$, using the parameters in (4.1), (4.6), (4.7), and (4.9). The top panels show that ![]() $\dot {M}$ increases approximately linearly with
$\dot {M}$ increases approximately linearly with ![]() $B_r(\mbox {1 a.u.})$ at fixed
$B_r(\mbox {1 a.u.})$ at fixed ![]() $f_{\textrm {max}, \textrm {WS}}$, and that
$f_{\textrm {max}, \textrm {WS}}$, and that ![]() $U_\infty$ varies only weakly with
$U_\infty$ varies only weakly with ![]() $B_r(\mbox {1 a.u.})$, consistent with measurements from the Ulysses spacecraft (Schwadron & McComas Reference Schwadron and McComas2008; Riley et al. Reference Riley, Mikic, Lionello, Linker, Schwadron and McComas2010). The left panel of the middle row shows that
$B_r(\mbox {1 a.u.})$, consistent with measurements from the Ulysses spacecraft (Schwadron & McComas Reference Schwadron and McComas2008; Riley et al. Reference Riley, Mikic, Lionello, Linker, Schwadron and McComas2010). The left panel of the middle row shows that ![]() $r_\textrm {A}$ depends more strongly on
$r_\textrm {A}$ depends more strongly on ![]() $B_r(\mbox {1 a.u.})$ than on
$B_r(\mbox {1 a.u.})$ than on ![]() $f_{\textrm {max}, \textrm {WS}}$, whereas the reverse is true for
$f_{\textrm {max}, \textrm {WS}}$, whereas the reverse is true for ![]() $r_\textrm {c}$. As in figure 6,
$r_\textrm {c}$. As in figure 6, ![]() $\overline {c_\textrm {s}}$ varies very weakly across the entire parameter range observed. The lower-right panel shows that, when (4.9) holds,
$\overline {c_\textrm {s}}$ varies very weakly across the entire parameter range observed. The lower-right panel shows that, when (4.9) holds, ![]() $\chi _\textrm {H}$ depends more strongly on
$\chi _\textrm {H}$ depends more strongly on ![]() $f_{\textrm {max}, \textrm {WS}}$ than on
$f_{\textrm {max}, \textrm {WS}}$ than on ![]() $B_r(\mbox {1 a.u.})$.
$B_r(\mbox {1 a.u.})$.
5. Discussion and conclusion
The main goal of this paper is to obtain an approximate analytic solution to the coupled problems of coronal heating and solar-wind acceleration under the assumption that the solar wind is powered primarily by an AW energy flux. Section 2 presents a first step toward this goal, namely, a simplified calculation of ![]() $\dot {M}$,
$\dot {M}$, ![]() $U_{\infty }$, and the coronal temperature in a spherically symmetric, steady-state solar wind in the absence of solar rotation. This calculation is based upon: (1) the assumption that
$U_{\infty }$, and the coronal temperature in a spherically symmetric, steady-state solar wind in the absence of solar rotation. This calculation is based upon: (1) the assumption that ![]() $p\,\textrm {d} V$ work rather than thermal conduction is the primary sink of internal energy in the sub-Alfvénic region as a whole; (2) the result of § 3.2.2 that a solar or stellar wind heated primarily by AW turbulence becomes approximately isothermal between the coronal base
$p\,\textrm {d} V$ work rather than thermal conduction is the primary sink of internal energy in the sub-Alfvénic region as a whole; (2) the result of § 3.2.2 that a solar or stellar wind heated primarily by AW turbulence becomes approximately isothermal between the coronal base ![]() $r_\textrm {b}$ and Alfvén critical point
$r_\textrm {b}$ and Alfvén critical point ![]() $r_\textrm {A}$; and (3) the finding in recent direct numerical simulations that most of the AW power at the coronal base
$r_\textrm {A}$; and (3) the finding in recent direct numerical simulations that most of the AW power at the coronal base ![]() $P_\textrm {AW}(r_\textrm {b})$ is dissipated between
$P_\textrm {AW}(r_\textrm {b})$ is dissipated between ![]() $r=r_\textrm {b}$ and
$r=r_\textrm {b}$ and ![]() $r=r_\textrm {A}$ (Perez et al. Reference Perez, Chandran, Klein and Martinovic2021). The calculation of § 2 shows that
$r=r_\textrm {A}$ (Perez et al. Reference Perez, Chandran, Klein and Martinovic2021). The calculation of § 2 shows that
Deviations from (5.1) can be caused by a number of factors, including conductive losses into the transition region, wave momentum deposition inside the wave-modified sonic-critical point, and the fact that part of the AW power reaches the super-Alfvénic region, where it enhances ![]() $U_{\infty }$ without contributing to the heating that helps drive the outflow of mass past the wave-modified sonic critical point. These factors are accounted for in the more detailed solar-wind model developed in § 3. It is worth noting that in this model:
$U_{\infty }$ without contributing to the heating that helps drive the outflow of mass past the wave-modified sonic critical point. These factors are accounted for in the more detailed solar-wind model developed in § 3. It is worth noting that in this model:
(i) the plasma density at the coronal base
 $\rho (r_\textrm {b}) = \rho _\textrm {b}$ is determined by equating the turbulent heating rate
$\rho (r_\textrm {b}) = \rho _\textrm {b}$ is determined by equating the turbulent heating rate  $Q(r_\textrm {b})$ and radiative cooling rate
$Q(r_\textrm {b})$ and radiative cooling rate  $R(r_\textrm {b})$; and
$R(r_\textrm {b})$; and(ii) an analytic solution for the heat flux from the corona into the transition region
 $q_\textrm {b}$ is obtained by balancing, within the transition region, conductive heating against internal-energy losses from
$q_\textrm {b}$ is obtained by balancing, within the transition region, conductive heating against internal-energy losses from  $p\,\textrm {d} V$ work, advection, and radiative cooling.
$p\,\textrm {d} V$ work, advection, and radiative cooling.
The expression (3.57) for ![]() $\rho _\textrm {b}$ that results from setting
$\rho _\textrm {b}$ that results from setting ![]() $Q(r_\textrm {b}) = R(r_\textrm {b})$ contains a factor of
$Q(r_\textrm {b}) = R(r_\textrm {b})$ contains a factor of ![]() $x^{1/4}$, where
$x^{1/4}$, where ![]() $x = \overline { c_\textrm {s}}^2/v_\textrm {esc}^2$ is the dimensionless temperature. Thus,
$x = \overline { c_\textrm {s}}^2/v_\textrm {esc}^2$ is the dimensionless temperature. Thus, ![]() $x$ must be found before the exact value of
$x$ must be found before the exact value of ![]() $\rho _\textrm {b}$ can be determined. However, because
$\rho _\textrm {b}$ can be determined. However, because ![]() $\dot {M}$ is so sensitive to the coronal temperature,
$\dot {M}$ is so sensitive to the coronal temperature, ![]() $x^{1/4}$ can to a good approximation be treated as a constant (see, e.g. figures 6 and 7), and (3.57) with
$x^{1/4}$ can to a good approximation be treated as a constant (see, e.g. figures 6 and 7), and (3.57) with ![]() $x^{1/4} = 0.44$ can be used to obtain the approximate value of
$x^{1/4} = 0.44$ can be used to obtain the approximate value of ![]() $\rho _\textrm {b}$ without solving the full model equations.
$\rho _\textrm {b}$ without solving the full model equations.
The equations of the solar-wind model developed in § 3 are solved analytically in two different parameter regimes. One of these is the conduction-dominated limit, in which heat conduction into the transition region is the dominant mechanism for draining internal energy from the sub-Alfvénic region, wave pressure makes the dominant contribution to the critical-point velocity ![]() $U_\textrm {c}$ in (3.89), and the wave-energy term dominates over the plasma-internal-energy term in the Bernoulli equation (3.95). This limit corresponds to photospheric velocities much smaller than those of the Sun. The second parameter regime is the expansion-dominated limit, in which
$U_\textrm {c}$ in (3.89), and the wave-energy term dominates over the plasma-internal-energy term in the Bernoulli equation (3.95). This limit corresponds to photospheric velocities much smaller than those of the Sun. The second parameter regime is the expansion-dominated limit, in which ![]() $p\,\textrm {d} V$ work is the dominant sink of internal energy in the sub-Alfvénic region, the sound speed makes the dominant contribution to the critical-point velocity
$p\,\textrm {d} V$ work is the dominant sink of internal energy in the sub-Alfvénic region, the sound speed makes the dominant contribution to the critical-point velocity ![]() $U_\textrm {c}$ in (3.89), and the plasma-internal-energy term in the Bernoulli integral (3.95) dominates over the wave-energy term. As illustrated in figure 4, the expansion-dominated regime is relevant to the solar wind. The leading-order solution in the expansion-dominated regime reproduces (5.1), with a small difference in the coronal temperature arising from the fact that
$U_\textrm {c}$ in (3.89), and the plasma-internal-energy term in the Bernoulli integral (3.95) dominates over the wave-energy term. As illustrated in figure 4, the expansion-dominated regime is relevant to the solar wind. The leading-order solution in the expansion-dominated regime reproduces (5.1), with a small difference in the coronal temperature arising from the fact that ![]() $\delta v_\textrm {b}$ has a weak dependence on the coronal temperature in the model of § 3. Numerical solutions to the model equations approach the approximate analytic solutions in the appropriate parameter regimes, match a range of solar-wind observations, and illustrate how the properties of the solar wind depend upon the r.m.s. photospheric velocity, super-radial expansion factor, and interplanetary magnetic-field strength.
$\delta v_\textrm {b}$ has a weak dependence on the coronal temperature in the model of § 3. Numerical solutions to the model equations approach the approximate analytic solutions in the appropriate parameter regimes, match a range of solar-wind observations, and illustrate how the properties of the solar wind depend upon the r.m.s. photospheric velocity, super-radial expansion factor, and interplanetary magnetic-field strength.
5.1. Top-down causality for determining  $\dot {M}$,
$\dot {M}$,  $q_{\rm b}$, and the pressure, temperature range, and altitude of the transition region within the solar atmosphere
$q_{\rm b}$, and the pressure, temperature range, and altitude of the transition region within the solar atmosphere
In this paper, as in Parker's original model (Parker Reference Parker1958, Reference Parker1965), the average rate at which mass flows out through the lower solar atmosphere is determined in large part by the outflow condition at the wave-modified sonic critical point ![]() $r_\textrm {c}$, several
$r_\textrm {c}$, several ![]() $R_\odot$ out from the Sun, at which the plasma transitions from being gravitationally bound to gravitationally unbound. Since the gravitational force weakens with increasing
$R_\odot$ out from the Sun, at which the plasma transitions from being gravitationally bound to gravitationally unbound. Since the gravitational force weakens with increasing ![]() $r$, there is no physical mechanism that can prevent plasma at
$r$, there is no physical mechanism that can prevent plasma at ![]() $r_\textrm {c}$ from flowing outward at approximately the wave-enhanced effective sound speed,
$r_\textrm {c}$ from flowing outward at approximately the wave-enhanced effective sound speed, ![]() $c_\textrm {s, eff} \equiv \displaystyle [(p + p_\textrm {wave})/\rho ]^{1/2} = [ c_\textrm {s}^2 + 0.5 (\delta v)^2]^{1/2}$, evaluated at
$c_\textrm {s, eff} \equiv \displaystyle [(p + p_\textrm {wave})/\rho ]^{1/2} = [ c_\textrm {s}^2 + 0.5 (\delta v)^2]^{1/2}$, evaluated at ![]() $r=r_\textrm {c}$, which is comparable to the square root of the right-hand side of (3.89). This is why
$r=r_\textrm {c}$, which is comparable to the square root of the right-hand side of (3.89). This is why ![]() $\dot {M} \sim A(r_\textrm {c}) \rho _\textrm {c} c_{\textrm {s}, \textrm {eff}}(r_\textrm {c})$.
$\dot {M} \sim A(r_\textrm {c}) \rho _\textrm {c} c_{\textrm {s}, \textrm {eff}}(r_\textrm {c})$.
On the other hand, localised motions near the transition region at speeds ![]() $\ll v_\textrm {esc}$ are gravitationally bound, and the mass flux that they carry is not determinative of
$\ll v_\textrm {esc}$ are gravitationally bound, and the mass flux that they carry is not determinative of ![]() $\dot {M}$. For example, if at some time, such motions led to an overall mass outflow rate at
$\dot {M}$. For example, if at some time, such motions led to an overall mass outflow rate at ![]() $r_\textrm {b}$ exceeding the rate
$r_\textrm {b}$ exceeding the rate ![]() $\sim A(r_\textrm {c}) \rho _\textrm {c} c_{\textrm {s}, \textrm {eff}}(r_\textrm {c})$ at which mass flows past the critical point
$\sim A(r_\textrm {c}) \rho _\textrm {c} c_{\textrm {s}, \textrm {eff}}(r_\textrm {c})$ at which mass flows past the critical point ![]() $r_\textrm {c}$, then plasma would build up in the corona. This would, in turn, weaken the pressure gradient relative to the gravitational force per unit volume in the vicinity of the transition region, thereby reducing the amount of plasma flowing up from the chromosphere.
$r_\textrm {c}$, then plasma would build up in the corona. This would, in turn, weaken the pressure gradient relative to the gravitational force per unit volume in the vicinity of the transition region, thereby reducing the amount of plasma flowing up from the chromosphere.
Nevertheless, the transition region and chromosphere do affect ![]() $\dot {M}$ in two ways. First,
$\dot {M}$ in two ways. First, ![]() $q_\textrm {b}$ reduces the net heating power within the quasi-isothermal sub-Alfvénic region,
$q_\textrm {b}$ reduces the net heating power within the quasi-isothermal sub-Alfvénic region, ![]() $P_\textrm {net}$. As discussed following (2.16), the heating cost per unit mass for plasma to transit the quasi-isothermal sub-Alfvénic region is
$P_\textrm {net}$. As discussed following (2.16), the heating cost per unit mass for plasma to transit the quasi-isothermal sub-Alfvénic region is ![]() $\overline { c_\textrm {s}}^2 \ln (\rho _\textrm {b}/\rho (r_\textrm {A})) \simeq v_\textrm {esc}^2$, and
$\overline { c_\textrm {s}}^2 \ln (\rho _\textrm {b}/\rho (r_\textrm {A})) \simeq v_\textrm {esc}^2$, and ![]() $\dot {M} \simeq P_\textrm {net}/v_\textrm {esc}^2$. By reducing
$\dot {M} \simeq P_\textrm {net}/v_\textrm {esc}^2$. By reducing ![]() $P_\textrm {net}$, the conduction of heat from the corona into the transition region reduces
$P_\textrm {net}$, the conduction of heat from the corona into the transition region reduces ![]() $\dot {M}$. The second way that the lower solar atmosphere affects
$\dot {M}$. The second way that the lower solar atmosphere affects ![]() $\dot {M}$ is via the chromospheric/transition-region transmission coefficient,
$\dot {M}$ is via the chromospheric/transition-region transmission coefficient, ![]() $f_\textrm {chr} = P_\textrm {AW}(r_\textrm {b})/P_\textrm {AW}(R_{\odot })$, whose value again influences the value of
$f_\textrm {chr} = P_\textrm {AW}(r_\textrm {b})/P_\textrm {AW}(R_{\odot })$, whose value again influences the value of ![]() $P_\textrm {net}$. To summarise this paragraph and the preceding paragraph, the chromosphere and transition region influence
$P_\textrm {net}$. To summarise this paragraph and the preceding paragraph, the chromosphere and transition region influence ![]() $\dot {M}$ thermodynamically, but not dynamically.
$\dot {M}$ thermodynamically, but not dynamically.
The regulation of the mass flux at ![]() $r_\textrm {b}$ by the critical-point condition at
$r_\textrm {b}$ by the critical-point condition at ![]() $r_\textrm {c}$ is an example of ‘top-down’ causality, in which physical processes at larger
$r_\textrm {c}$ is an example of ‘top-down’ causality, in which physical processes at larger ![]() $r$ control the plasma properties at smaller
$r$ control the plasma properties at smaller ![]() $r$. In the model of this paper, top-down causality also characterises the determination of
$r$. In the model of this paper, top-down causality also characterises the determination of ![]() $q_\textrm {b}$, the pressure within the transition region, the altitude of the transition region in the solar atmosphere, and the temperature jump across the transition region. As mentioned previously,
$q_\textrm {b}$, the pressure within the transition region, the altitude of the transition region in the solar atmosphere, and the temperature jump across the transition region. As mentioned previously, ![]() $\rho _\textrm {b}$ is determined by the condition that
$\rho _\textrm {b}$ is determined by the condition that ![]() $Q(r_\textrm {b}) = R(r_\textrm {b})$, without reference to conditions in the chromosphere or the value of
$Q(r_\textrm {b}) = R(r_\textrm {b})$, without reference to conditions in the chromosphere or the value of ![]() $q_\textrm {b}$. The sound speed at
$q_\textrm {b}$. The sound speed at ![]() $r=r_\textrm {b}$, which is
$r=r_\textrm {b}$, which is ![]() $\simeq \overline {c_\textrm {s}}$, is approximately determined by balancing turbulent heating against internal-energy losses from
$\simeq \overline {c_\textrm {s}}$, is approximately determined by balancing turbulent heating against internal-energy losses from ![]() $p\,\textrm {d} V$ work within the corona and sub-Alfvénic solar wind. The outflow velocity at
$p\,\textrm {d} V$ work within the corona and sub-Alfvénic solar wind. The outflow velocity at ![]() $r=r_\textrm {b}$,
$r=r_\textrm {b}$, ![]() $U_\textrm {b}$, follows from the value of
$U_\textrm {b}$, follows from the value of ![]() $\dot {M}$, which is controlled by the critical-point condition, as described above. The values of
$\dot {M}$, which is controlled by the critical-point condition, as described above. The values of ![]() $\rho _\textrm {b}$,
$\rho _\textrm {b}$, ![]() $\overline { c_\textrm {s}}$, and
$\overline { c_\textrm {s}}$, and ![]() $U_\textrm {b}$ jointly determine
$U_\textrm {b}$ jointly determine ![]() $q_\textrm {b}$ via (3.82), which embodies the requirement that conductive heating offset internal-energy losses (from radiation,
$q_\textrm {b}$ via (3.82), which embodies the requirement that conductive heating offset internal-energy losses (from radiation, ![]() $p\,\textrm {d} V$ work, and advection) within the transition region. The values of
$p\,\textrm {d} V$ work, and advection) within the transition region. The values of ![]() $\rho _\textrm {b}$ and
$\rho _\textrm {b}$ and ![]() $\overline { c_\textrm {s}}$ are sufficient to determine the approximate transition-region pressure,
$\overline { c_\textrm {s}}$ are sufficient to determine the approximate transition-region pressure, ![]() $p_\textrm {tr} \simeq \rho _\textrm {b} \overline { c_\textrm {s}}^2$. The pressure within the upper chromosphere,
$p_\textrm {tr} \simeq \rho _\textrm {b} \overline { c_\textrm {s}}^2$. The pressure within the upper chromosphere, ![]() $p_\textrm {chr}(r)$, is an approximately exponentially decreasing function of altitude. The altitude of the transition region is determined by setting
$p_\textrm {chr}(r)$, is an approximately exponentially decreasing function of altitude. The altitude of the transition region is determined by setting ![]() $p_\textrm {chr}(r)= p_\textrm {tr}$. The shape of the radiative loss function plotted in figure 2 constrains the temperature at the bottom of the transition region to be approximately
$p_\textrm {chr}(r)= p_\textrm {tr}$. The shape of the radiative loss function plotted in figure 2 constrains the temperature at the bottom of the transition region to be approximately ![]() $10^4$ K, so that radiative cooling within the comparatively dense upper chromosphere can be balanced by local heating mechanisms in the absence of strong conductive heating. Given this constraint, the factor by which the temperature changes across the transition region is determined by the value of
$10^4$ K, so that radiative cooling within the comparatively dense upper chromosphere can be balanced by local heating mechanisms in the absence of strong conductive heating. Given this constraint, the factor by which the temperature changes across the transition region is determined by the value of ![]() $T(r_\textrm {b})$, which is controlled by the balance between heating and
$T(r_\textrm {b})$, which is controlled by the balance between heating and ![]() $p\,\textrm {d} V$ work in the corona, as discussed previously.
$p\,\textrm {d} V$ work in the corona, as discussed previously.
Although the condition ![]() $R(r_\textrm {b}) = Q(r_\textrm {b})$ determines the density
$R(r_\textrm {b}) = Q(r_\textrm {b})$ determines the density ![]() $\rho _\textrm {b}$ at the upper boundary of the transition region within the corona (subject to the caveats at the end of the paragraph following (5.1)), setting
$\rho _\textrm {b}$ at the upper boundary of the transition region within the corona (subject to the caveats at the end of the paragraph following (5.1)), setting ![]() $R(r)=Q(r)$ within the chromosphere does not determine the density at the lower edge of the transition region, because small changes in
$R(r)=Q(r)$ within the chromosphere does not determine the density at the lower edge of the transition region, because small changes in ![]() $T$ within the upper chromosphere lead to dramatic changes in the radiative loss function
$T$ within the upper chromosphere lead to dramatic changes in the radiative loss function ![]() $\varLambda (T)$, as shown in figure 2. The density at the bottom of the transition region is instead largely determined by the values of
$\varLambda (T)$, as shown in figure 2. The density at the bottom of the transition region is instead largely determined by the values of ![]() $\rho _\textrm {b}$ and
$\rho _\textrm {b}$ and ![]() $\overline {c_\textrm {s}}$, the near constancy of the pressure across the transition region, and the above-mentioned constraint (arising from the shape of the radiative loss function) that
$\overline {c_\textrm {s}}$, the near constancy of the pressure across the transition region, and the above-mentioned constraint (arising from the shape of the radiative loss function) that ![]() $T\sim 10^4$ K in the upper chromosphere.
$T\sim 10^4$ K in the upper chromosphere.
5.2. Limitations and future work
The model of § 3 has a number of shortcomings. First, the sub-Alfvénic region is not truly isothermal, and, hence, the quasi-isothermal approximation in (2.5) leads to some error. Second, for the solutions shown in figure 5, the temperature ![]() $m_\textrm {p} \overline {c_\textrm {s}}^2/(2k_\textrm {B})$ of the sub-Alfvénic region increases from
$m_\textrm {p} \overline {c_\textrm {s}}^2/(2k_\textrm {B})$ of the sub-Alfvénic region increases from ![]() $\simeq 7\times 10^5 \mbox { K}$ when
$\simeq 7\times 10^5 \mbox { K}$ when ![]() $U_\infty \simeq 800 \mbox { km} \mbox { s}^{-1}$ to
$U_\infty \simeq 800 \mbox { km} \mbox { s}^{-1}$ to ![]() $\simeq 8.4 \times 10^5 \mbox { K}$ when
$\simeq 8.4 \times 10^5 \mbox { K}$ when ![]() $U_\infty \simeq 400 \mbox { km} \mbox { s}^{-1}$. In contrast, in measurements from the Ulysses spacecraft, the coronal freeze-in temperature increases from
$U_\infty \simeq 400 \mbox { km} \mbox { s}^{-1}$. In contrast, in measurements from the Ulysses spacecraft, the coronal freeze-in temperature increases from ![]() $\simeq 9 \times 10^5 \mbox { K}$ when
$\simeq 9 \times 10^5 \mbox { K}$ when ![]() $U_{\infty } \simeq 800 \mbox { km} \mbox { s}^{-1}$ to
$U_{\infty } \simeq 800 \mbox { km} \mbox { s}^{-1}$ to ![]() $\simeq 1.35 \times 10^6 \mbox { K}$ when
$\simeq 1.35 \times 10^6 \mbox { K}$ when ![]() $U_\infty \simeq 400 \mbox { km} \mbox { s}^{-1}$ (McComas et al. Reference McComas, Elliott, Gosling, Reisenfeld, Skoug, Goldstein, Neugebauer and Balogh2002; Schwadron & McComas Reference Schwadron and McComas2003). Although the numerical solutions in figure 5 reproduce the observed anti-correlation between coronal temperature and asymptotic wind speed, the isothermal-sub-Alfvénic-region approximation of the present paper is too crude to be able match the measured freeze-in temperatures in detail. Another shortcoming is that the dimensionless coefficient
$U_\infty \simeq 400 \mbox { km} \mbox { s}^{-1}$ (McComas et al. Reference McComas, Elliott, Gosling, Reisenfeld, Skoug, Goldstein, Neugebauer and Balogh2002; Schwadron & McComas Reference Schwadron and McComas2003). Although the numerical solutions in figure 5 reproduce the observed anti-correlation between coronal temperature and asymptotic wind speed, the isothermal-sub-Alfvénic-region approximation of the present paper is too crude to be able match the measured freeze-in temperatures in detail. Another shortcoming is that the dimensionless coefficient ![]() $\sigma$ that appears in the turbulent heating rate has a large impact on the solution to the model equations, but is an adjustable free parameter. Further work is needed to provide a physical basis for determining
$\sigma$ that appears in the turbulent heating rate has a large impact on the solution to the model equations, but is an adjustable free parameter. Further work is needed to provide a physical basis for determining ![]() $\sigma$ and how it varies from one flux tube to another.
$\sigma$ and how it varies from one flux tube to another.
In a future study, the model developed in § 3 could be used in conjunction with studies that map the magnetic-field line traversed by PSP back to a source region on the Sun to rapidly predict flow properties at PSP's location based on the observed super-radial expansion factor within the source region (see, e.g. Bale et al. Reference Bale, Badman, Bonnell, Bowen, Burgess, Case, Cattell, Chandran, Chaston and Chen2019; Kasper et al. Reference Kasper, Bale, Belcher, Berthomier, Case, Chandran, Curtis, Gallagher, Gary and Golub2019). In addition, the modelling results and approaches developed in this paper could be applied to outflows from other astrophysical objects, such as stars with differing masses and winds from accretion disks around compact astrophysical objects.
Acknowledgements
I thank Sam Badman, Stuart Bale, Chris Chen, Eugene Churazov, Joe Hollweg, Justin Kasper, Brian Metzger, Jean Perez, Eliot Quataert, Alex Schekochihin, and Marco Velli for valuable discussions, and the two anonymous referees for comments that led to improvements in the manuscript. This work was supported in part by NASA grant NNN06AA01C to the Parker Solar Probe FIELDS Experiment and by NASA grants NNX17AI18G and 80NSSC19K0829.
Editor William Dorland thanks the referees for their advice in evaluating this article.
Declaration of interests
The author reports no conflict of interest.
Appendix A. Solving for  $U(r)$ and
$U(r)$ and  $r_\textrm {A}$
$r_\textrm {A}$
Once ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$ are determined by solving (3.67), (3.94), and (3.97), the value of
$x$ are determined by solving (3.67), (3.94), and (3.97), the value of ![]() $U(r)$ between
$U(r)$ between ![]() $r=r_\textrm {b}$ and
$r=r_\textrm {b}$ and ![]() $r=r_\textrm {A}$ (which is as yet unknown) can be found by solving the Bernoulli integral (3.95) with
$r=r_\textrm {A}$ (which is as yet unknown) can be found by solving the Bernoulli integral (3.95) with ![]() $\varGamma$ given by (3.96). An equation for
$\varGamma$ given by (3.96). An equation for ![]() $r_\textrm {A}$ can be obtained by evaluating the Bernoulli integral (3.95) at
$r_\textrm {A}$ can be obtained by evaluating the Bernoulli integral (3.95) at ![]() $r=r_\textrm {A}$, setting
$r=r_\textrm {A}$, setting ![]() $U(r_\textrm {A}) = v_\textrm {A}(r_\textrm {A})$ and
$U(r_\textrm {A}) = v_\textrm {A}(r_\textrm {A})$ and ![]() $y=1$, and rewriting
$y=1$, and rewriting ![]() $\varGamma$ using (3.96), which leads to
$\varGamma$ using (3.96), which leads to
 \begin{align} 0 &= \frac{v_\textrm{A}(r_\textrm{A})^2}{2} - 2 \overline{ c_\textrm{s}}^2 \ln y_\textrm{b} + \frac{v_\textrm{esc}^2}{2} \left(\psi^{1/2} - \frac{R_{{\odot}}}{r_\textrm{A}}\right)\nonumber\\ &\quad - \frac{(\delta v_\textrm{b})^2}{2(1-\sigma)} \left[ \frac{2^{\sigma -2}(3+\sigma)(1+y_\textrm{b})^{2-\sigma} -2}{y_\textrm{b}} - 1 - \sigma\right] - \frac{v_\textrm{Ab}^2}{2 y_\textrm{b}^2}. \end{align}
\begin{align} 0 &= \frac{v_\textrm{A}(r_\textrm{A})^2}{2} - 2 \overline{ c_\textrm{s}}^2 \ln y_\textrm{b} + \frac{v_\textrm{esc}^2}{2} \left(\psi^{1/2} - \frac{R_{{\odot}}}{r_\textrm{A}}\right)\nonumber\\ &\quad - \frac{(\delta v_\textrm{b})^2}{2(1-\sigma)} \left[ \frac{2^{\sigma -2}(3+\sigma)(1+y_\textrm{b})^{2-\sigma} -2}{y_\textrm{b}} - 1 - \sigma\right] - \frac{v_\textrm{Ab}^2}{2 y_\textrm{b}^2}. \end{align}Upon setting
in (A 1) and rewriting ![]() $v_\textrm {Ab}$ in (A 1) using (3.63), one obtains the following equation for
$v_\textrm {Ab}$ in (A 1) using (3.63), one obtains the following equation for ![]() $r_\textrm {A}$:
$r_\textrm {A}$:
 \begin{align} 0 &= \left[\frac{y_\textrm{b}^2 \eta(r_\textrm{A})^2}{(x \tilde{\rho}_\odot)^{1/4} \xi^2 \psi^{1/2}}\right] \left(\frac{R_{{\odot}}}{r_\textrm{A}}\right)^{4} - \frac{R_{{\odot}}}{r_\textrm{A}} - 4 x \ln y_\textrm{b} + \psi^{1/2} - \frac{\psi^{3/2} \eta_\textrm{b}^2}{(x \tilde{\rho}_\odot)^{1/4} \xi^2 y_\textrm{b}^2}\nonumber\\ &\quad + \frac{\epsilon}{1-\sigma} \left[\frac{2 - 2^{\sigma - 2}(3+\sigma)(1+y_\textrm{b})^{2-\sigma}}{y_\textrm{b}} + 1+\sigma \right]. \end{align}
\begin{align} 0 &= \left[\frac{y_\textrm{b}^2 \eta(r_\textrm{A})^2}{(x \tilde{\rho}_\odot)^{1/4} \xi^2 \psi^{1/2}}\right] \left(\frac{R_{{\odot}}}{r_\textrm{A}}\right)^{4} - \frac{R_{{\odot}}}{r_\textrm{A}} - 4 x \ln y_\textrm{b} + \psi^{1/2} - \frac{\psi^{3/2} \eta_\textrm{b}^2}{(x \tilde{\rho}_\odot)^{1/4} \xi^2 y_\textrm{b}^2}\nonumber\\ &\quad + \frac{\epsilon}{1-\sigma} \left[\frac{2 - 2^{\sigma - 2}(3+\sigma)(1+y_\textrm{b})^{2-\sigma}}{y_\textrm{b}} + 1+\sigma \right]. \end{align} At ![]() $r> r_\textrm {A}$, the outflow velocity
$r> r_\textrm {A}$, the outflow velocity ![]() $U(r)$ cannot be determined from the Bernoulli integral, because the quasi-isothermal approximation does not apply. In addition, (3.40) yields a poor approximation for
$U(r)$ cannot be determined from the Bernoulli integral, because the quasi-isothermal approximation does not apply. In addition, (3.40) yields a poor approximation for ![]() $z_-$ at
$z_-$ at ![]() $r>r_\textrm {A}$, because
$r>r_\textrm {A}$, because ![]() $1+y$ approaches a constant when
$1+y$ approaches a constant when ![]() $r \gg r_\textrm {A}$. A better approximation for
$r \gg r_\textrm {A}$. A better approximation for ![]() $z_-$ in the super-Alfvénic region can be obtained from (3.25) and the simplifying approximation that
$z_-$ in the super-Alfvénic region can be obtained from (3.25) and the simplifying approximation that ![]() $|(\textrm {d} / \textrm {d} r) \ln (v_\textrm {A})| = -(\textrm {d} /\textrm {d} r) \ln y$, which holds when
$|(\textrm {d} / \textrm {d} r) \ln (v_\textrm {A})| = -(\textrm {d} /\textrm {d} r) \ln y$, which holds when ![]() $B\propto r^{-2}$ and
$B\propto r^{-2}$ and ![]() $\rho \propto r^{-2}$ (the latter scalings being fairly accurate for
$\rho \propto r^{-2}$ (the latter scalings being fairly accurate for ![]() $10 R_{\odot } \lesssim r \lesssim 60 R_{\odot }$, a region in which the field lines are approximately radial and the flow speed is approximately constant). In this case, (3.25) becomes
$10 R_{\odot } \lesssim r \lesssim 60 R_{\odot }$, a region in which the field lines are approximately radial and the flow speed is approximately constant). In this case, (3.25) becomes
Integrating (3.21) from ![]() $r=r_\textrm {A}$ out to larger
$r=r_\textrm {A}$ out to larger ![]() $r$ then gives
$r$ then gives ![]() $z_+^2 = [z_+(r_\textrm {A})]^2 4y^2 / (1+y)^2$, where the value of
$z_+^2 = [z_+(r_\textrm {A})]^2 4y^2 / (1+y)^2$, where the value of ![]() $z_+(r_\textrm {A})$ is obtained by setting
$z_+(r_\textrm {A})$ is obtained by setting ![]() $y=1$ in (3.41). The approximate value of
$y=1$ in (3.41). The approximate value of ![]() $c_\textrm {s}^2(r)$ can then be found in terms of
$c_\textrm {s}^2(r)$ can then be found in terms of ![]() $\rho$ by solving the internal-energy equation (3.32) with
$\rho$ by solving the internal-energy equation (3.32) with ![]() $Q$ given by (3.22) and neglecting radiative cooling and thermal conduction. This leads to
$Q$ given by (3.22) and neglecting radiative cooling and thermal conduction. This leads to
 \begin{equation} c_\textrm{s}^2(r) = \left[\frac{\rho(r)}{\rho_\textrm{A}}\right]^{\gamma-1} \left(\overline{ c_\textrm{s}}^2 + K \int_y^1 \frac{y_1^{3-2\gamma}\, \textrm{d} y_1}{1+y_1} \right) \end{equation}
\begin{equation} c_\textrm{s}^2(r) = \left[\frac{\rho(r)}{\rho_\textrm{A}}\right]^{\gamma-1} \left(\overline{ c_\textrm{s}}^2 + K \int_y^1 \frac{y_1^{3-2\gamma}\, \textrm{d} y_1}{1+y_1} \right) \end{equation}
at ![]() $r>r_\textrm {A}$, where
$r>r_\textrm {A}$, where
Total-energy conservation implies that the mechanical luminosity
is independent of ![]() $r$, where the ratio of specific heats
$r$, where the ratio of specific heats ![]() $\gamma$ has been set equal to
$\gamma$ has been set equal to ![]() $5/3$. The value of
$5/3$. The value of ![]() $U(r)$ at
$U(r)$ at ![]() $r>r_\textrm {A}$ can be obtained by setting
$r>r_\textrm {A}$ can be obtained by setting
and rewriting ![]() $\rho (r)$ in terms of
$\rho (r)$ in terms of ![]() $U(r)$ using (3.7); i.e.
$U(r)$ using (3.7); i.e. ![]() $\rho (r) U(r)/B(r) = \rho _\textrm {b} U_\textrm {b}/ B_\textrm {b}$. As
$\rho (r) U(r)/B(r) = \rho _\textrm {b} U_\textrm {b}/ B_\textrm {b}$. As ![]() $U(r_\textrm {A}) = v_\textrm {A}(r_\textrm {A})$ and
$U(r_\textrm {A}) = v_\textrm {A}(r_\textrm {A})$ and ![]() $y(r_\textrm {A}) = 1$, (A 7) implies that
$y(r_\textrm {A}) = 1$, (A 7) implies that
Determining ![]() $U(r)$ at
$U(r)$ at ![]() $r>r_\textrm {A}$ via (A 7) through (A 9) requires evaluating
$r>r_\textrm {A}$ via (A 7) through (A 9) requires evaluating ![]() $r_\textrm {A}$ and
$r_\textrm {A}$ and ![]() $v_\textrm {A}(r_\textrm {A})$. An alternative method that avoids this requirement results from noting that
$v_\textrm {A}(r_\textrm {A})$. An alternative method that avoids this requirement results from noting that
 \begin{align} L_\textrm{mech}(r_\textrm{b})= \dot{M}\left\{ \frac{v_\textrm{Ab}^2}{2y_\textrm{b}^2} + \frac{5 \overline{c_\textrm{s}^2}}{2} - \frac{v_\textrm{esc}^2 \psi^{1/2}}{2} + (\delta v_\textrm{b})^2 \left[ \frac{1}{2} + (1+y_\textrm{b})(1 - \chi_\textrm{H})\right] + 2 \overline{c_\textrm{s}}^2 \ln y_\textrm{b}\right\}, \end{align}
\begin{align} L_\textrm{mech}(r_\textrm{b})= \dot{M}\left\{ \frac{v_\textrm{Ab}^2}{2y_\textrm{b}^2} + \frac{5 \overline{c_\textrm{s}^2}}{2} - \frac{v_\textrm{esc}^2 \psi^{1/2}}{2} + (\delta v_\textrm{b})^2 \left[ \frac{1}{2} + (1+y_\textrm{b})(1 - \chi_\textrm{H})\right] + 2 \overline{c_\textrm{s}}^2 \ln y_\textrm{b}\right\}, \end{align}
where (3.66) has been used to eliminate ![]() $q_\textrm {b}$. Replacing
$q_\textrm {b}$. Replacing ![]() $\chi _\textrm {H}$ in (A 10) with the expression on the right-hand side of (3.45) leads to the consistency check that
$\chi _\textrm {H}$ in (A 10) with the expression on the right-hand side of (3.45) leads to the consistency check that
Combining (A 8) and (A 11), one can find ![]() $U(r)$ at
$U(r)$ at ![]() $r>r_\textrm {A}$ by setting
$r>r_\textrm {A}$ by setting
Equation (A 12) leads to a simple expression for the asymptotic wind velocity ![]() $U_{\infty }$, i.e.
$U_{\infty }$, i.e. ![]() $U(r)$ as
$U(r)$ as ![]() $r\rightarrow \infty$. As
$r\rightarrow \infty$. As ![]() $r\rightarrow \infty$, the kinetic-energy flux dominates the total energy flux, and
$r\rightarrow \infty$, the kinetic-energy flux dominates the total energy flux, and ![]() $L_\textrm {mech}(r) \rightarrow \dot {M} U_{\infty }^2 / 2$. Setting
$L_\textrm {mech}(r) \rightarrow \dot {M} U_{\infty }^2 / 2$. Setting ![]() $\dot {M} U_{\infty }^2/2 = L_\textrm {mech}(r_\textrm {b})$ yields
$\dot {M} U_{\infty }^2/2 = L_\textrm {mech}(r_\textrm {b})$ yields
 \begin{equation} U_{\infty} = \left[\frac{v_\textrm{Ab}^2}{y_\textrm{b}^2} + 5 \overline{ c_\textrm{s}}^2 - v_\textrm{esc}^2 \psi^{1/2} + 2 (\delta v_\textrm{b})^2 \left( \frac{3}{2} + y_\textrm{b}\right) - \frac{2 q_\textrm{b} y_\textrm{b}}{\rho_\textrm{b} v_\textrm{Ab}}\right]^{1/2}. \end{equation}
\begin{equation} U_{\infty} = \left[\frac{v_\textrm{Ab}^2}{y_\textrm{b}^2} + 5 \overline{ c_\textrm{s}}^2 - v_\textrm{esc}^2 \psi^{1/2} + 2 (\delta v_\textrm{b})^2 \left( \frac{3}{2} + y_\textrm{b}\right) - \frac{2 q_\textrm{b} y_\textrm{b}}{\rho_\textrm{b} v_\textrm{Ab}}\right]^{1/2}. \end{equation}Appendix B. Approximate analytic solutions
As discussed in § 3.8, the core of the solar-wind model developed in § 3 is a set of three simultaneous equations, (3.67), (3.94), and (3.97), for the three unknowns ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$. In this section, two different approximate analytic solutions to these equations are obtained in two different parameter regimes. Both solutions rely on the simplifying approximations in (3.100), which are repeated here:
$x$. In this section, two different approximate analytic solutions to these equations are obtained in two different parameter regimes. Both solutions rely on the simplifying approximations in (3.100), which are repeated here:
In particular, ![]() $y_\textrm {b}$ is taken to be sufficiently large that: (1) the
$y_\textrm {b}$ is taken to be sufficiently large that: (1) the ![]() $U_\textrm {b}^2 = v_\textrm {Ab}^2/y_\textrm {b}^2$ term in (3.96) can be dropped, which amounts to dropping the second-to-last term on the left-hand side of (3.97); and (2)
$U_\textrm {b}^2 = v_\textrm {Ab}^2/y_\textrm {b}^2$ term in (3.96) can be dropped, which amounts to dropping the second-to-last term on the left-hand side of (3.97); and (2) ![]() $O(y_\textrm {b}^{-1})$ terms can be dropped in (3.45), so that
$O(y_\textrm {b}^{-1})$ terms can be dropped in (3.45), so that
where
The ![]() $y_\textrm {b}^{-\sigma }$ term in (B 2) is retained, even though terms of order
$y_\textrm {b}^{-\sigma }$ term in (B 2) is retained, even though terms of order ![]() $y_\textrm {b}^{-1}$ are discarded, on the working assumption that
$y_\textrm {b}^{-1}$ are discarded, on the working assumption that ![]() $\sigma \sim 0.1\text {--}0.5$, as is the case in the numerical examples in § 4. As mentioned in § 3.8, the last equality in (B 1) amounts to taking all of the super-radial expansion of the field lines to occur inside the wave-modified sonic critical point and the field lines to be completely radial at
$\sigma \sim 0.1\text {--}0.5$, as is the case in the numerical examples in § 4. As mentioned in § 3.8, the last equality in (B 1) amounts to taking all of the super-radial expansion of the field lines to occur inside the wave-modified sonic critical point and the field lines to be completely radial at ![]() $r\geqslant r_\textrm {c}$. With these approximations, (3.67), (3.94), and (3.97) become, respectively,
$r\geqslant r_\textrm {c}$. With these approximations, (3.67), (3.94), and (3.97) become, respectively,
 \begin{gather} \frac{\epsilon_\odot \tilde{\rho}_{{\odot}}^{3/8} \chi_\textrm{H}}{B_\ast \xi x^{1/8}} - \frac{2 x \ln y_\textrm{b}}{y_\textrm{b}} - \frac{q_\textrm{b}}{\rho_\textrm{b} v_\textrm{Ab} v_\textrm{esc}^2} = 0, \end{gather}
\begin{gather} \frac{\epsilon_\odot \tilde{\rho}_{{\odot}}^{3/8} \chi_\textrm{H}}{B_\ast \xi x^{1/8}} - \frac{2 x \ln y_\textrm{b}}{y_\textrm{b}} - \frac{q_\textrm{b}}{\rho_\textrm{b} v_\textrm{Ab} v_\textrm{esc}^2} = 0, \end{gather} \begin{gather} \left(\frac{y_\textrm{c}^2 x^{1/8} \xi \tilde{\rho}_{{\odot}}^{1/8}}{16 y_\textrm{b}}\right)^{2/3} - x - \frac{\epsilon_\odot \tilde{\rho}_\odot^{3/8} y_\textrm{b}^{1-\sigma}[y_\textrm{c}^2(1+\sigma) + 3y_\textrm{c}]}{4 B_\ast \xi x^{1/8}(1+y_\textrm{c})^{3-\sigma}}= 0, \end{gather}
\begin{gather} \left(\frac{y_\textrm{c}^2 x^{1/8} \xi \tilde{\rho}_{{\odot}}^{1/8}}{16 y_\textrm{b}}\right)^{2/3} - x - \frac{\epsilon_\odot \tilde{\rho}_\odot^{3/8} y_\textrm{b}^{1-\sigma}[y_\textrm{c}^2(1+\sigma) + 3y_\textrm{c}]}{4 B_\ast \xi x^{1/8}(1+y_\textrm{c})^{3-\sigma}}= 0, \end{gather}and
 \begin{equation} 1 - x\left[4 \ln \left(\frac{y_\textrm{b}}{y_\textrm{c}}\right) + 3\right] - \frac{\epsilon_\odot \tilde{\rho}_\odot^{3/8} y_\textrm{b}^{1-\sigma}[y_\textrm{c}^2(1+\sigma)(7-3\sigma) + y_\textrm{c}(21 - 5\sigma) + 8]}{4(1-\sigma)B_\ast \xi x^{1/8} (1+y_\textrm{c})^{3-\sigma}} = 0. \end{equation}
\begin{equation} 1 - x\left[4 \ln \left(\frac{y_\textrm{b}}{y_\textrm{c}}\right) + 3\right] - \frac{\epsilon_\odot \tilde{\rho}_\odot^{3/8} y_\textrm{b}^{1-\sigma}[y_\textrm{c}^2(1+\sigma)(7-3\sigma) + y_\textrm{c}(21 - 5\sigma) + 8]}{4(1-\sigma)B_\ast \xi x^{1/8} (1+y_\textrm{c})^{3-\sigma}} = 0. \end{equation}B.1. Conduction-dominated limit
When ![]() $\epsilon _\odot$ is sufficiently small, an approximate solution to (B 4), (B 5), and (B 6) can be obtained through the method of dominant balance (Bender & Orszag Reference Bender and Orszag1978), in which two of the three terms in each equation are taken to be dominant, and the third term is taken to be much smaller in magnitude. Neglecting the smaller term in each equation yields the leading-order solution, with the smaller term producing higher-order corrections. In the present case, it is the second term on the left-hand side of each equation that can be neglected to leading order. In (B 4), this corresponds to balancing turbulent heating of the sub-Alfvénic region against the heat that is conducted from the corona into the transition region. In other words, conduction into the transition region rather than
$\epsilon _\odot$ is sufficiently small, an approximate solution to (B 4), (B 5), and (B 6) can be obtained through the method of dominant balance (Bender & Orszag Reference Bender and Orszag1978), in which two of the three terms in each equation are taken to be dominant, and the third term is taken to be much smaller in magnitude. Neglecting the smaller term in each equation yields the leading-order solution, with the smaller term producing higher-order corrections. In the present case, it is the second term on the left-hand side of each equation that can be neglected to leading order. In (B 4), this corresponds to balancing turbulent heating of the sub-Alfvénic region against the heat that is conducted from the corona into the transition region. In other words, conduction into the transition region rather than ![]() $p\,\textrm {d} V$ work is the dominant sink of internal energy in the sub-Alfvénic region as a whole. Neglecting the second term in (B 5) amounts to assuming that the fluctuating velocity makes the dominant contribution to
$p\,\textrm {d} V$ work is the dominant sink of internal energy in the sub-Alfvénic region as a whole. Neglecting the second term in (B 5) amounts to assuming that the fluctuating velocity makes the dominant contribution to ![]() $U_\textrm {c}$ in (3.89), which is equivalent to taking
$U_\textrm {c}$ in (3.89), which is equivalent to taking ![]() $\delta v(r_\textrm {c}) \gg \overline {c_\textrm {s}}$. The latter equality appears paradoxical, because the small-
$\delta v(r_\textrm {c}) \gg \overline {c_\textrm {s}}$. The latter equality appears paradoxical, because the small-![]() $\epsilon _\odot$ limit corresponds to small values of the fluctuating velocity at the coronal base. However, as
$\epsilon _\odot$ limit corresponds to small values of the fluctuating velocity at the coronal base. However, as ![]() $\epsilon _\odot \rightarrow 0$, the coronal temperature drops, the density scale height in the corona decreases, and the wave amplitude at the critical point grows as the AWs attempt to conserve wave action, which would lead to
$\epsilon _\odot \rightarrow 0$, the coronal temperature drops, the density scale height in the corona decreases, and the wave amplitude at the critical point grows as the AWs attempt to conserve wave action, which would lead to ![]() $\delta v \propto \rho ^{-1/4}$ when
$\delta v \propto \rho ^{-1/4}$ when ![]() $U\ll v_\textrm {A}$ in the absence of reflection and dissipation (see (3.19) and (3.20)). Neglecting the second term in (B 6) amounts to taking the wave pressure force to have a larger cumulative effect than the thermal pressure force on the acceleration of the outflowing plasma between
$U\ll v_\textrm {A}$ in the absence of reflection and dissipation (see (3.19) and (3.20)). Neglecting the second term in (B 6) amounts to taking the wave pressure force to have a larger cumulative effect than the thermal pressure force on the acceleration of the outflowing plasma between ![]() $r_\textrm {b}$ and
$r_\textrm {b}$ and ![]() $r_\textrm {c}$, which can again be understood as a consequence of the wave amplitudes growing rapidly with increasing
$r_\textrm {c}$, which can again be understood as a consequence of the wave amplitudes growing rapidly with increasing ![]() $r$ when the density scale height in the corona is small.
$r$ when the density scale height in the corona is small.
As already noted in (3.101) and illustrated in figure 4, ![]() $\dot {M}$ is exceedingly small in the conduction-dominated limit, and as a consequence
$\dot {M}$ is exceedingly small in the conduction-dominated limit, and as a consequence ![]() $U_\textrm {b} \ll \overline { c_\textrm {s}}$. The heat flux at the coronal base is thus approximately given by (3.83), and (B 4) can be rewritten as
$U_\textrm {b} \ll \overline { c_\textrm {s}}$. The heat flux at the coronal base is thus approximately given by (3.83), and (B 4) can be rewritten as
 \begin{equation} \frac{\epsilon_\odot \tilde{\rho}_{{\odot}}^{3/8} \chi_\textrm{H}}{B_\ast \xi x^{1/8}} - \frac{2 x \ln y_\textrm{b}}{y_\textrm{b}} - \frac{I_1 x^{13/8} \xi \tilde{\rho}_\odot^{1/8}}{\eta_\textrm{b}} = 0. \end{equation}
\begin{equation} \frac{\epsilon_\odot \tilde{\rho}_{{\odot}}^{3/8} \chi_\textrm{H}}{B_\ast \xi x^{1/8}} - \frac{2 x \ln y_\textrm{b}}{y_\textrm{b}} - \frac{I_1 x^{13/8} \xi \tilde{\rho}_\odot^{1/8}}{\eta_\textrm{b}} = 0. \end{equation}
Balancing the first and third terms in (B 7) and dropping the ![]() $y_\textrm {b}^{-\sigma }$ term in (B 2) yields the leading-order solution for the dimensionless temperature in the sub-Alfvénic region:
$y_\textrm {b}^{-\sigma }$ term in (B 2) yields the leading-order solution for the dimensionless temperature in the sub-Alfvénic region:
Anticipating the solution for y c, it is useful to predict at the outset (as will shortly be confirmed by (B 10) and (B 11)) that
Balancing the first and third terms in (B 6) then gives
 \begin{equation} \frac{y_\textrm{b}}{y_\textrm{c}} = \left[ \frac{4(1-\sigma) B_\ast^{2/7} \eta_\textrm{b}^{2/7}} {I_1^{1/14}(1+\sigma)(7-3\sigma)\epsilon_\odot^{5/7}\tilde{l}_\textrm{b}^{3/14}\tilde{\rho}_\odot^{5/14}} \right]^{1/(1-\sigma)}. \end{equation}
\begin{equation} \frac{y_\textrm{b}}{y_\textrm{c}} = \left[ \frac{4(1-\sigma) B_\ast^{2/7} \eta_\textrm{b}^{2/7}} {I_1^{1/14}(1+\sigma)(7-3\sigma)\epsilon_\odot^{5/7}\tilde{l}_\textrm{b}^{3/14}\tilde{\rho}_\odot^{5/14}} \right]^{1/(1-\sigma)}. \end{equation}
Balancing the first and third terms in (B 5) and making use of (B 9) and (B 10), one arrives at the leading-order solution for ![]() $y_\textrm {b}$:
$y_\textrm {b}$:
where
 \begin{equation} I_2 = 16 I_1^{-(1+\sigma)/(14-14\sigma)} \left(\frac{4}{1+\sigma}\right)^{2/(1-\sigma)} \left(\frac{1-\sigma}{7-3\sigma}\right)^{(7-3\sigma)/(2-2\sigma)} . \end{equation}
\begin{equation} I_2 = 16 I_1^{-(1+\sigma)/(14-14\sigma)} \left(\frac{4}{1+\sigma}\right)^{2/(1-\sigma)} \left(\frac{1-\sigma}{7-3\sigma}\right)^{(7-3\sigma)/(2-2\sigma)} . \end{equation}
Equations (3.13), (3.57), (B 8), and (B 11) then yield the leading-order mass outflow rate in the conduction-dominated regime, ![]() $\dot {M}^\textrm {(cond)}$, given in (3.101).
$\dot {M}^\textrm {(cond)}$, given in (3.101).
The asymptotic wind velocity ![]() $U_\infty$ is obtained by setting
$U_\infty$ is obtained by setting ![]() $\dot {M} U_\infty ^2 /2$ equal to the mechanical luminosity at the coronal base
$\dot {M} U_\infty ^2 /2$ equal to the mechanical luminosity at the coronal base ![]() $L_\textrm {mech}(r_\textrm {b})$ as described in Appendix A, where
$L_\textrm {mech}(r_\textrm {b})$ as described in Appendix A, where ![]() $L_\textrm {mech}$ is defined in (A 7). When this procedure is carried out using (B 8) and (B 11), the two leading-order terms in
$L_\textrm {mech}$ is defined in (A 7). When this procedure is carried out using (B 8) and (B 11), the two leading-order terms in ![]() $L_\textrm {mech}(r_\textrm {b})$ cancel. To obtain the leading-order non-vanishing term in
$L_\textrm {mech}(r_\textrm {b})$ cancel. To obtain the leading-order non-vanishing term in ![]() $U_{\infty }^2$, one must account for the next largest term in (B 7), which results from the
$U_{\infty }^2$, one must account for the next largest term in (B 7), which results from the ![]() $\chi _\textrm {H}$ correction; i.e. the second term on the right-hand side of (B 2). When this term is retained, one obtains the leading-order asymptotic wind speed in the conduction-dominated regime,
$\chi _\textrm {H}$ correction; i.e. the second term on the right-hand side of (B 2). When this term is retained, one obtains the leading-order asymptotic wind speed in the conduction-dominated regime, ![]() $U_{\infty }^\textrm {(cond)}$, given in (3.102).
$U_{\infty }^\textrm {(cond)}$, given in (3.102).
The range of ![]() $\epsilon _\odot$ values for which (3.101), (3.102), (B 8), (B 10), and (B 11) are approximately valid can be determined by requiring that the neglected terms in (B 5), (B 6), and (B 7) be small compared to the other terms when
$\epsilon _\odot$ values for which (3.101), (3.102), (B 8), (B 10), and (B 11) are approximately valid can be determined by requiring that the neglected terms in (B 5), (B 6), and (B 7) be small compared to the other terms when ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$ are given by (B 8), (B 10), and (B 11). The most stringent condition on
$x$ are given by (B 8), (B 10), and (B 11). The most stringent condition on ![]() $\epsilon _{\odot }$ arises from carrying out this procedure for (B 6), which results in the requirement that
$\epsilon _{\odot }$ arises from carrying out this procedure for (B 6), which results in the requirement that
where ![]() $I_3 = I_1^{-4/7} \tilde {\rho }_{\odot }^{1/7} (\eta _\textrm {b} B_\ast \tilde {l}_\textrm {b})^{2/7}$, and
$I_3 = I_1^{-4/7} \tilde {\rho }_{\odot }^{1/7} (\eta _\textrm {b} B_\ast \tilde {l}_\textrm {b})^{2/7}$, and ![]() $I_4$ equals the right-hand side of (B 10) without the
$I_4$ equals the right-hand side of (B 10) without the ![]() $\epsilon _{\odot }$ term; i.e.
$\epsilon _{\odot }$ term; i.e. ![]() $I_4 = \epsilon _\odot ^{5/(7-7\sigma )} y_\textrm {b}/y_\textrm {c}$, with
$I_4 = \epsilon _\odot ^{5/(7-7\sigma )} y_\textrm {b}/y_\textrm {c}$, with ![]() $y_\textrm {b}/y_\textrm {c}$ given by the right-hand side of (B 10). Upon neglecting the quantity
$y_\textrm {b}/y_\textrm {c}$ given by the right-hand side of (B 10). Upon neglecting the quantity ![]() $4\ln I_4 + 3$ on the left-hand side of (B 13), which is smaller in magnitude than the remaining term when
$4\ln I_4 + 3$ on the left-hand side of (B 13), which is smaller in magnitude than the remaining term when ![]() $\epsilon _\odot$ is in the conduction-dominated regime but other parameters take on Sun-like values, one finds that the conduction-dominated regime corresponds to
$\epsilon _\odot$ is in the conduction-dominated regime but other parameters take on Sun-like values, one finds that the conduction-dominated regime corresponds to
where ![]() $W_{-1}$ is the lower branch of the Lambert
$W_{-1}$ is the lower branch of the Lambert ![]() $W$ function.
$W$ function.
B.2. Expansion-dominated limit
In the expansion-dominated limit, the first two terms on the left-hand sides of (B 4), (B 5), and (B 6) are treated as dominant. For this case, it is useful to define the variables
where
 \begin{equation} A_1 = \frac{\epsilon_{{\odot}}^{3/4} \tilde{\rho}_\odot^{3/8} \tilde{l}_\textrm{b}^{1/4}}{(\eta_\textrm{b} B_\ast)^{1/4}}. \end{equation}
\begin{equation} A_1 = \frac{\epsilon_{{\odot}}^{3/4} \tilde{\rho}_\odot^{3/8} \tilde{l}_\textrm{b}^{1/4}}{(\eta_\textrm{b} B_\ast)^{1/4}}. \end{equation}
Rewriting (B 4), (B 5), and (B 6) in terms of ![]() $u$,
$u$, ![]() $p$, and
$p$, and ![]() $x$ rather than
$x$ rather than ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$, one obtains
$x$, one obtains
 \begin{gather} \left(\frac{u x^{1/4} \xi \tilde{\rho}_\odot^{1/8}}{16 A_1 p^2}\right)^{2/3} - x = b, \end{gather}
\begin{gather} \left(\frac{u x^{1/4} \xi \tilde{\rho}_\odot^{1/8}}{16 A_1 p^2}\right)^{2/3} - x = b, \end{gather}and
The quantities ![]() $a$,
$a$, ![]() $b$, and
$b$, and ![]() $c$, which are treated as small, are functions of
$c$, which are treated as small, are functions of ![]() $u$,
$u$, ![]() $p$, and
$p$, and ![]() $x$. In order to see how (B 17), (B 18), and (B 19) follow from (B 4), (B 5), and (B 6), it is helpful to leave terms containing
$x$. In order to see how (B 17), (B 18), and (B 19) follow from (B 4), (B 5), and (B 6), it is helpful to leave terms containing ![]() $y_\textrm {b}$ and
$y_\textrm {b}$ and ![]() $y_\textrm {c}$ in the expressions for
$y_\textrm {c}$ in the expressions for ![]() $a$,
$a$, ![]() $b$, and
$b$, and ![]() $c$, with the understanding that
$c$, with the understanding that ![]() $y_\textrm {b} = x^{1/8} u / A_1$ and
$y_\textrm {b} = x^{1/8} u / A_1$ and ![]() $y_\textrm {c} = x^{1/8} u / (A_1 p)$:
$y_\textrm {c} = x^{1/8} u / (A_1 p)$:
 \begin{gather} b \equiv \frac{\epsilon_\odot \tilde{\rho}_\odot^{3/8} y_\textrm{b}^{1-\sigma}[y_\textrm{c}^2(1+\sigma) + 3 y_\textrm{c}]}{4 B_\ast \xi x^{1/8} (1+y_\textrm{c})^{3-\sigma}} , \end{gather}
\begin{gather} b \equiv \frac{\epsilon_\odot \tilde{\rho}_\odot^{3/8} y_\textrm{b}^{1-\sigma}[y_\textrm{c}^2(1+\sigma) + 3 y_\textrm{c}]}{4 B_\ast \xi x^{1/8} (1+y_\textrm{c})^{3-\sigma}} , \end{gather}and
 \begin{equation} c \equiv \frac{\epsilon_\odot \tilde{\rho}_\odot^{3/8} y_\textrm{b}^{1-\sigma}[y_\textrm{c}^2(1+\sigma)(7-3\sigma) + y_\textrm{c}(21-5\sigma) + 8]}{4 (1-\sigma) B_\ast \xi x^{1/8} (1+y_\textrm{c})^{3-\sigma}}. \end{equation}
\begin{equation} c \equiv \frac{\epsilon_\odot \tilde{\rho}_\odot^{3/8} y_\textrm{b}^{1-\sigma}[y_\textrm{c}^2(1+\sigma)(7-3\sigma) + y_\textrm{c}(21-5\sigma) + 8]}{4 (1-\sigma) B_\ast \xi x^{1/8} (1+y_\textrm{c})^{3-\sigma}}. \end{equation}From (B 17), it follows that
Equation (B 19) implies that
After substituting (B 23) and (B 24) into (B 18), one finds that
where
 \begin{align} S(u, a, b, c) &= \frac{c}{u} - a - \frac{(1-a)}{\ln A_1}\left[ \frac{5}{4} \ln u\right.\nonumber\\ &\quad \left. + \frac{\ln (1-a)}{4} - \frac{\ln({-}2\ln A_1)}{4} - \ln A_2 + \frac{3}{2} - \frac{3}{2} \ln \left(b - \frac{(1-a)u}{2\ln A_1}\right)\right], \end{align}
\begin{align} S(u, a, b, c) &= \frac{c}{u} - a - \frac{(1-a)}{\ln A_1}\left[ \frac{5}{4} \ln u\right.\nonumber\\ &\quad \left. + \frac{\ln (1-a)}{4} - \frac{\ln({-}2\ln A_1)}{4} - \ln A_2 + \frac{3}{2} - \frac{3}{2} \ln \left(b - \frac{(1-a)u}{2\ln A_1}\right)\right], \end{align}and
which is ![]() $\simeq 1$ for typical solar parameters. The quantities
$\simeq 1$ for typical solar parameters. The quantities ![]() $a$,
$a$, ![]() $b$, and
$b$, and ![]() $c$ are themselves functions of
$c$ are themselves functions of ![]() $u$ by virtue of (B 15) and (B 20) through (B 24).
$u$ by virtue of (B 15) and (B 20) through (B 24).
In the expansion-dominated regime
The latter inequality is achieved when ![]() $-1 / \ln A_1$,
$-1 / \ln A_1$, ![]() $|a|$,
$|a|$, ![]() $b$, and
$b$, and ![]() $c$ are much smaller than
$c$ are much smaller than ![]() $1$. When (B 28) is satisfied, (B 23), (B 24), and (B 25) can be solved perturbatively through the recursion relations
$1$. When (B 28) is satisfied, (B 23), (B 24), and (B 25) can be solved perturbatively through the recursion relations
 \begin{align} \frac{1}{u_n} - 1 & = \left\{\begin{array}{@{}cc} 0 & \mbox{ if } n=0 \\ S(u_{n-1}, a_{n-1}, b_{n-1}, c_{n-1}) & \mbox{ if } n\geqslant 1 \end{array} \right. \end{align}
\begin{align} \frac{1}{u_n} - 1 & = \left\{\begin{array}{@{}cc} 0 & \mbox{ if } n=0 \\ S(u_{n-1}, a_{n-1}, b_{n-1}, c_{n-1}) & \mbox{ if } n\geqslant 1 \end{array} \right. \end{align}
where ![]() $n= 0, 1, 2, \dots$, and
$n= 0, 1, 2, \dots$, and ![]() $a_{-1} = c_{-1} = 0$. The values of
$a_{-1} = c_{-1} = 0$. The values of ![]() $a_n$,
$a_n$, ![]() $b_n$, and
$b_n$, and ![]() $c_n$ are obtained by replacing
$c_n$ are obtained by replacing ![]() $(a,b,c,u,y_\textrm {b}, y_\textrm {c}, x)$ with
$(a,b,c,u,y_\textrm {b}, y_\textrm {c}, x)$ with ![]() $(a_n, b_n, c_n, u_n,y_{\textrm {b},n}, y_{\textrm {c}, n}, x_n)$ in (B 20), (B 21), and (B 22). For reference below, the values of
$(a_n, b_n, c_n, u_n,y_{\textrm {b},n}, y_{\textrm {c}, n}, x_n)$ in (B 20), (B 21), and (B 22). For reference below, the values of ![]() $\rho _\textrm {b}$,
$\rho _\textrm {b}$, ![]() $v_\textrm {Ab}$, and
$v_\textrm {Ab}$, and ![]() $q_\textrm {b}$ that result from this substitution (via (3.57), (3.63), and (3.82)) are denoted
$q_\textrm {b}$ that result from this substitution (via (3.57), (3.63), and (3.82)) are denoted ![]() $\rho _{\textrm {b}, n}$,
$\rho _{\textrm {b}, n}$, ![]() $v_{\textrm {Ab}, n}$, and
$v_{\textrm {Ab}, n}$, and ![]() $q_{\textrm {b},n}$. The values of
$q_{\textrm {b},n}$. The values of ![]() $y_{\textrm {b},n}$ and
$y_{\textrm {b},n}$ and ![]() $y_{\textrm {c},n}$ are obtained by replacing
$y_{\textrm {c},n}$ are obtained by replacing ![]() $(y_\textrm {b}, y_\textrm {c}, x, u, p)$ with
$(y_\textrm {b}, y_\textrm {c}, x, u, p)$ with ![]() $(y_{\textrm {b},n}, y_{\textrm {c},n}, x_n, u_n, p_n)$ in (B 15).
$(y_{\textrm {b},n}, y_{\textrm {c},n}, x_n, u_n, p_n)$ in (B 15).
The ![]() $n^\textrm {th}$-order approximation for
$n^\textrm {th}$-order approximation for ![]() $\dot {M}$ in the expansion-dominated regime, denoted
$\dot {M}$ in the expansion-dominated regime, denoted ![]() $\dot {M}^\textrm {(exp)}_n$, can be found by setting
$\dot {M}^\textrm {(exp)}_n$, can be found by setting ![]() $\dot {M} = \dot {M}^\textrm {(exp)}_n$,
$\dot {M} = \dot {M}^\textrm {(exp)}_n$, ![]() $x=x_\textrm {n}$,
$x=x_\textrm {n}$, ![]() $y_\textrm {b} = y_{\textrm {b},n}$ and
$y_\textrm {b} = y_{\textrm {b},n}$ and ![]() $\psi = 1$ in (3.99):
$\psi = 1$ in (3.99):
For ![]() $n\geqslant 1$, I define the
$n\geqslant 1$, I define the ![]() $n^\textrm {th}$-order approximation for
$n^\textrm {th}$-order approximation for ![]() $U_\infty$, denoted
$U_\infty$, denoted ![]() $U_{\infty , n}^\textrm {(exp)}$, to be the value of
$U_{\infty , n}^\textrm {(exp)}$, to be the value of ![]() $U_{\infty }$ in (A 13) when
$U_{\infty }$ in (A 13) when ![]() $(x, y_\textrm {b}, \psi , q_\textrm {b}, \rho _\textrm {b}, v_\textrm {Ab}) = (x_n, y_{\textrm {b},n}, 1, q_{\textrm {b},n}, \rho _{\textrm {b},n}, v_{\textrm {Ab},n})$:
$(x, y_\textrm {b}, \psi , q_\textrm {b}, \rho _\textrm {b}, v_\textrm {Ab}) = (x_n, y_{\textrm {b},n}, 1, q_{\textrm {b},n}, \rho _{\textrm {b},n}, v_{\textrm {Ab},n})$:
 \begin{equation} U_{\infty, n}^\textrm{(exp)} = v_\textrm{esc} \left[ \frac{v_{\textrm{Ab}, n}^2}{y_{\textrm{b}, n}^2 v_\textrm{esc}^2} + 5 x_n - 1 + \frac{2y_{\textrm{b},n} \epsilon_\odot \tilde{\rho}_\odot^{3/8} }{B_\ast \xi x_n^{1/8}} - \frac{2 q_{\textrm{b},n} y_{\textrm{b},n}}{\rho_{\textrm{b},n} v_{\textrm{Ab},n} v_\textrm{esc}^2} \right]^{1/2}, \end{equation}
\begin{equation} U_{\infty, n}^\textrm{(exp)} = v_\textrm{esc} \left[ \frac{v_{\textrm{Ab}, n}^2}{y_{\textrm{b}, n}^2 v_\textrm{esc}^2} + 5 x_n - 1 + \frac{2y_{\textrm{b},n} \epsilon_\odot \tilde{\rho}_\odot^{3/8} }{B_\ast \xi x_n^{1/8}} - \frac{2 q_{\textrm{b},n} y_{\textrm{b},n}}{\rho_{\textrm{b},n} v_{\textrm{Ab},n} v_\textrm{esc}^2} \right]^{1/2}, \end{equation}
where I have invoked (B 1) to approximate ![]() $3/2 + y_{\textrm {b}, n}$ as
$3/2 + y_{\textrm {b}, n}$ as ![]() $y_{\textrm {b},n}$. The leading-order approximation for
$y_{\textrm {b},n}$. The leading-order approximation for ![]() $U_\infty$ in the expansion-dominated regime, denoted
$U_\infty$ in the expansion-dominated regime, denoted ![]() $U_{\infty , 0}^\textrm {(exp)}$, is obtained from (B 33) with
$U_{\infty , 0}^\textrm {(exp)}$, is obtained from (B 33) with ![]() $n=0$ after dropping terms that were neglected in the calculation of
$n=0$ after dropping terms that were neglected in the calculation of ![]() $u_0$ – in particular, the first, second, and last terms inside the brackets on the right-hand side of (B 33). This yields
$u_0$ – in particular, the first, second, and last terms inside the brackets on the right-hand side of (B 33). This yields
As in the conduction-dominated limit, the range of ![]() $\epsilon _\odot$ values for which (B 29), (B 32), and (B 34) are approximately valid can be determined by imposing the constraint that the neglected terms in (B 4), (B 5), and (B 6) be small compared to the terms that are kept when
$\epsilon _\odot$ values for which (B 29), (B 32), and (B 34) are approximately valid can be determined by imposing the constraint that the neglected terms in (B 4), (B 5), and (B 6) be small compared to the terms that are kept when ![]() $y_\textrm {b}$,
$y_\textrm {b}$, ![]() $y_\textrm {c}$, and
$y_\textrm {c}$, and ![]() $x$ are given by (B 15), (B 16), (B 23), (B 24), and
$x$ are given by (B 15), (B 16), (B 23), (B 24), and ![]() $u=1$. Carrying out this procedure for (B 4) and making the simplifying approximations that
$u=1$. Carrying out this procedure for (B 4) and making the simplifying approximations that ![]() $a$ is dominated by the last term on the right-hand side of (B 20), that
$a$ is dominated by the last term on the right-hand side of (B 20), that ![]() $q_\textrm {b}$ is given by (3.83), and that
$q_\textrm {b}$ is given by (3.83), and that ![]() $\ln A_1 \simeq \ln (\epsilon _\odot ^{3/4})$, one obtains the requirement that
$\ln A_1 \simeq \ln (\epsilon _\odot ^{3/4})$, one obtains the requirement that
 \begin{equation} \epsilon_\odot\ {\gg}\ \epsilon_{{\odot} \textrm{exp},\textrm{min}} \equiv \exp\left( \frac{7}{2} W_{{-}1}\left( - \frac{4 I_1^{1/14}}{21 \tilde{\rho}_{{\odot}}^{1/7} (\tilde{l}_\textrm{b} \eta_\textrm{b} B_\ast)^{2/7}}\right)\right), \end{equation}
\begin{equation} \epsilon_\odot\ {\gg}\ \epsilon_{{\odot} \textrm{exp},\textrm{min}} \equiv \exp\left( \frac{7}{2} W_{{-}1}\left( - \frac{4 I_1^{1/14}}{21 \tilde{\rho}_{{\odot}}^{1/7} (\tilde{l}_\textrm{b} \eta_\textrm{b} B_\ast)^{2/7}}\right)\right), \end{equation}
where ![]() $W_{-1}$ is, as above, the lower branch of the Lambert
$W_{-1}$ is, as above, the lower branch of the Lambert ![]() $W$ function. Equation (B 35) corresponds to the requirement that the conductive losses from the sub-Alfvénic region into the transition region be negligible compared to
$W$ function. Equation (B 35) corresponds to the requirement that the conductive losses from the sub-Alfvénic region into the transition region be negligible compared to ![]() $p\,\textrm {d} V$ work in this region. Carrying out the above procedure for (B 5) and again making the simplifying approximation that
$p\,\textrm {d} V$ work in this region. Carrying out the above procedure for (B 5) and again making the simplifying approximation that ![]() $\ln A_1 \simeq \ln ( \epsilon _\odot ^{3/4})$, one obtains
$\ln A_1 \simeq \ln ( \epsilon _\odot ^{3/4})$, one obtains
 \begin{align} \epsilon_\odot\ {\ll}\ \epsilon_{{\odot} \textrm{exp},\textrm{max}} \equiv \exp\left( \frac{3}{(1+\sigma)} W_{{-}1}\left( - \frac{2^{25/9} (1+\sigma)^{1/9} e^{2(1-\sigma)/3} }{9}\left[\frac{\eta_\textrm{b}B_\ast}{\tilde{l}_\textrm{b} \tilde{\rho}_{{\odot}}^{3/2}}\right]^{(1+\sigma)/9} \right) \right). \end{align}
\begin{align} \epsilon_\odot\ {\ll}\ \epsilon_{{\odot} \textrm{exp},\textrm{max}} \equiv \exp\left( \frac{3}{(1+\sigma)} W_{{-}1}\left( - \frac{2^{25/9} (1+\sigma)^{1/9} e^{2(1-\sigma)/3} }{9}\left[\frac{\eta_\textrm{b}B_\ast}{\tilde{l}_\textrm{b} \tilde{\rho}_{{\odot}}^{3/2}}\right]^{(1+\sigma)/9} \right) \right). \end{align}
Equation (B 36) corresponds to the requirement that the sound speed make the dominant contribution to the outflow velocity ![]() $U_\textrm {c}$ at the critical point in (3.89). As illustrated by the shaded gray rectangle in figure 4, for Sun-like parameters (and in particular, for
$U_\textrm {c}$ at the critical point in (3.89). As illustrated by the shaded gray rectangle in figure 4, for Sun-like parameters (and in particular, for ![]() $\eta _\textrm {b} = 30$),
$\eta _\textrm {b} = 30$), ![]() $\epsilon _{\odot \textrm {exp},\textrm {max}}$ is approximately four orders of magnitude larger than
$\epsilon _{\odot \textrm {exp},\textrm {max}}$ is approximately four orders of magnitude larger than ![]() $\epsilon _{\odot \textrm {exp}, \textrm {min}}$. There is thus a finite range of
$\epsilon _{\odot \textrm {exp}, \textrm {min}}$. There is thus a finite range of ![]() $\epsilon _\odot$ values that satisfy both (B 35) and (B 36). However, it should be noted that the approximations
$\epsilon _\odot$ values that satisfy both (B 35) and (B 36). However, it should be noted that the approximations ![]() $\ln A_1 \simeq \ln (\epsilon _\odot ^{3/4})$ and
$\ln A_1 \simeq \ln (\epsilon _\odot ^{3/4})$ and ![]() $q_\textrm {b} = I_1 \rho _\textrm {b} \overline {c_\textrm {s}}^3$ cause (B 35) to underestimate the lower bound on
$q_\textrm {b} = I_1 \rho _\textrm {b} \overline {c_\textrm {s}}^3$ cause (B 35) to underestimate the lower bound on ![]() $\epsilon _\odot$ in the expansion-dominated regime. Also, for Sun-like parameters, the assumption
$\epsilon _\odot$ in the expansion-dominated regime. Also, for Sun-like parameters, the assumption ![]() $r_\textrm {c} < r_\textrm {A}$ that underlies the model of § 3 breaks down at values of
$r_\textrm {c} < r_\textrm {A}$ that underlies the model of § 3 breaks down at values of ![]() $\epsilon _{\odot }$ smaller than
$\epsilon _{\odot }$ smaller than ![]() $\epsilon _{\odot \textrm {exp}, \textrm {max}}$, as illustrated in figure 4.
$\epsilon _{\odot \textrm {exp}, \textrm {max}}$, as illustrated in figure 4.