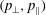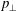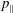1 Introduction
The vast majority of the visible matter in the universe is in the plasma state. The solar wind is an example of such an astrophysical plasma. Due to its accessibility to spacecraft, it is the perfect environment for making comparisons between theoretical plasma-physics predictions and in situ observations in the astrophysical context with access to wide scale separations (see, for example, Marsch Reference Marsch2006). Plasmas can deviate from thermodynamic equilibrium if the relaxation due to particle collisions occurs on time scales that are larger than the characteristic time scales of the collective plasma behaviour. Such a collisionless plasma is characterised by non-Maxwellian features in its velocity distribution functions. In the fast solar wind, this condition is frequently fulfilled, and, consequently, the observed distribution functions often deviate from the entropically favoured Maxwellian shape (Vasyliunas Reference Vasyliunas1968; Gosling et al. Reference Gosling, Asbridge, Bame, Feldman, Zwickl, Paschmann, Sckopke and Hynds1981; Lui & Krimigis Reference Lui and Krimigis1981; Marsch et al. Reference Marsch, Rosenbauer, Schwenn, Muehlhaeuser and Neubauer1982a ,Reference Marsch, Schwenn, Rosenbauer, Muehlhaeuser, Pilipp and Neubauer b ; Armstrong et al. Reference Armstrong, Paonessa, Bell and Krimigis1983; Lui & Krimigis Reference Lui and Krimigis1983; Christon et al. Reference Christon, Mitchell, Williams, Frank, Huang and Eastman1988; Williams, Mitchell & Christon Reference Williams, Mitchell and Christon1988). In particular, beams and temperature anisotropies are some of the observed features in the distributions of ions and electrons in the solar wind (Pilipp et al. Reference Pilipp, Muehlhaeuser, Miggenrieder, Montgomery and Rosenbauer1987a ,Reference Pilipp, Muehlhaeuser, Miggenrieder, Rosenbauer and Schwenn b ; Hellinger et al. Reference Hellinger, Trávníček, Kasper and Lazarus2006; Marsch Reference Marsch2006; Bale et al. Reference Bale, Kasper, Howes, Quataert, Salem and Sundkvist2009). If these deviations from equilibrium are suitably extreme, the plasma becomes unstable and generates waves or non-propagating structures that react back upon the plasma to reduce the deviations from equilibrium (Eviatar & Schulz Reference Eviatar and Schulz1970; Schwartz Reference Schwartz1980; Gary Reference Gary1993; Hellinger & Trávníček Reference Hellinger and Trávníček2011, Reference Hellinger and Trávníček2013). Also laboratory and fusion plasmas often show non-Maxwellian features in their velocity distribution functions. These include, for example, fast particles resulting from neutral-beam injections, alpha-particle beams from fusion reactions or non-Maxwellian distributions resulting from active ion/electron-cyclotron heating (Stix Reference Stix1975; Gaffey Reference Gaffey1976a ,Reference Gaffey b ; Tang Reference Tang1978; Seki et al. Reference Seki, Saigusa, Nemoto, Kusama, Tobita, Kuriyama and Uehara1989; Heidbrink & Sadler Reference Heidbrink and Sadler1994).
The behaviour of plasma waves and instabilities is typically studied with the help of numerical codes that solve the hot-plasma dispersion relation. Traditionally, these codes (like WHAMP, PLUME or NHDS) use a shifted bi-Maxwellian background distribution function as the zeroth-order description for the plasma state (Roennmark Reference Roennmark1982; Quataert Reference Quataert1998; Klein et al. Reference Klein, Howes, TenBarge, Bale, Chen and Salem2012; Verscharen & Chandran Reference Verscharen and Chandran2018). For nearly collisionless plasmas, however, the bi-Maxwellian distribution function is a mathematical convenience rather than a reliable representation of the true plasma distribution function, and many space-plasma observations show that the bi-Maxwellian representation is not accurate (Hundhausen Reference Hundhausen1970; Leubner Reference Leubner1978; Marsch et al. Reference Marsch, Schwenn, Rosenbauer, Muehlhaeuser, Pilipp and Neubauer1982b ; Pilipp et al. Reference Pilipp, Muehlhaeuser, Miggenrieder, Montgomery and Rosenbauer1987a ; Marsch & Tu Reference Marsch and Tu2001; Štverák et al. Reference Štverák, Maksimovic, Trávníček, Marsch, Fazakerley and Scime2009). Some previous approaches in non-Maxwellian solvers treated certain limits or geometries (Dum, Marsch & Pilipp Reference Dum, Marsch and Pilipp1980; Summers & Thorne Reference Summers and Thorne1991; Xue, Thorne & Summers Reference Xue, Thorne and Summers1993; Summers, Xue & Thorne Reference Summers, Xue and Thorne1994; Xue, Thorne & Summers Reference Xue, Thorne and Summers1996; Hellberg, Mace & Cattaert Reference Hellberg, Mace and Cattaert2005; Cattaert, Hellberg & Mace Reference Cattaert, Hellberg and Mace2007; Lazar & Poedts Reference Lazar and Poedts2009; Mace & Sydora Reference Mace and Sydora2010; Lazar, Poedts & Schlickeiser Reference Lazar, Poedts and Schlickeiser2011; Galvaõ et al. Reference Galvaõ, Ziebell, Gaelzer and de Juli2012; Xie Reference Xie2013; Lazar & Poedts Reference Lazar and Poedts2014; Gaelzer & Ziebell Reference Gaelzer and Ziebell2016; Gaelzer, Ziebell & Meneses Reference Gaelzer, Ziebell and Meneses2016) or faced challenges in the weakly damped limit (Hellinger & Trávníček Reference Hellinger and Trávníček2011).
We present our numerical code ALPS (Arbitrary Linear Plasma Solver), which solves the full hot-plasma dispersion relation in a plasma consisting of an arbitrary number of particle species with arbitrary background distribution functions
![]() $f_{0j}$
and with arbitrary directions of wave propagation with respect to the uniform background magnetic field. ALPS is also able to solve the dispersion relation for relativistic plasmas. Matsuda & Smith (Reference Matsuda and Smith1992) developed a code similar to ALPS that calculates the dispersion relation in an arbitrary plasma with relativistic effects. Their code uses a cubic-spline fit to both fill data gaps and approximate the analytic continuation, while ALPS uses a novel method called hybrid analytic continuation. The spline method forfeits its accuracy for strongly damped solutions since the calculation of the dispersion relation requires the evaluation of the spline at a complex value that is distant from the real grid points by which the spline is supported. Our method does not suffer from this problem. Astfalk & Jenko (Reference Astfalk and Jenko2017) also use a cubic-spline interpolation for the analytic continuation and as the basis for the integration in their code LEOPARD. This procedure allows for algebraic simplifications that enhance the speed of the integration significantly. LEOPARD, however, does not capture relativistic effects.
$f_{0j}$
and with arbitrary directions of wave propagation with respect to the uniform background magnetic field. ALPS is also able to solve the dispersion relation for relativistic plasmas. Matsuda & Smith (Reference Matsuda and Smith1992) developed a code similar to ALPS that calculates the dispersion relation in an arbitrary plasma with relativistic effects. Their code uses a cubic-spline fit to both fill data gaps and approximate the analytic continuation, while ALPS uses a novel method called hybrid analytic continuation. The spline method forfeits its accuracy for strongly damped solutions since the calculation of the dispersion relation requires the evaluation of the spline at a complex value that is distant from the real grid points by which the spline is supported. Our method does not suffer from this problem. Astfalk & Jenko (Reference Astfalk and Jenko2017) also use a cubic-spline interpolation for the analytic continuation and as the basis for the integration in their code LEOPARD. This procedure allows for algebraic simplifications that enhance the speed of the integration significantly. LEOPARD, however, does not capture relativistic effects.
In § 2, we review the underlying theory of the hot-plasma dispersion relation. § 3 presents ALPS’s numerical approach. In § 4, we compare ALPS results to known limits of the hot-plasma dispersion relation such as Maxwellian, bi-Maxwellian,
![]() $\unicode[STIX]{x1D705}$
-distributed, and relativistic pair plasmas. In § 5, we discuss our results and the applicability of ALPS to measured plasma distributions. The appendices describe how ALPS solutions depend on the resolution of the background distributions, discuss the Levenberg–Marquardt-fit routine used in our hybrid analytic continuation method and describe our strategy for numerically refining coarse-grained distribution functions obtained from spacecraft measurements.
$\unicode[STIX]{x1D705}$
-distributed, and relativistic pair plasmas. In § 5, we discuss our results and the applicability of ALPS to measured plasma distributions. The appendices describe how ALPS solutions depend on the resolution of the background distributions, discuss the Levenberg–Marquardt-fit routine used in our hybrid analytic continuation method and describe our strategy for numerically refining coarse-grained distribution functions obtained from spacecraft measurements.
2 The linear dispersion relation of a hot plasma
In this section, we discuss the mathematical basis for the calculation of the hot-plasma dispersion relation following the presentation and notation of Stix (Reference Stix1992). The determination of the kinetic wave dispersion relation in a hot plasma is based on the linearised set of Maxwell’s equations and the linearised Vlasov equation (Trubnikov Reference Trubnikov and Leontovich1959; Drummond & Rosenbluth Reference Drummond and Rosenbluth1963; Shkarofsky Reference Shkarofsky1966; Stix Reference Stix1992; Gary Reference Gary1993). A wave or instability is then associated with a first-order perturbation
![]() $\unicode[STIX]{x1D6FF}f_{j}$
in the distribution function of species
$\unicode[STIX]{x1D6FF}f_{j}$
in the distribution function of species
![]() $j$
about a prescribed time-averaged background distribution function
$j$
about a prescribed time-averaged background distribution function
![]() $f_{0j}$
,
$f_{0j}$
,
where
![]() $\boldsymbol{r}$
is the spatial coordinate and
$\boldsymbol{r}$
is the spatial coordinate and
![]() $\boldsymbol{p}$
is the momentum coordinate. As with the distribution function
$\boldsymbol{p}$
is the momentum coordinate. As with the distribution function
![]() $f_{j}$
in (2.1), we take the magnetic field
$f_{j}$
in (2.1), we take the magnetic field
![]() $\boldsymbol{B}$
to be the sum of a uniform background magnetic field
$\boldsymbol{B}$
to be the sum of a uniform background magnetic field
![]() $\boldsymbol{B}_{0}$
and a fluctuating magnetic field
$\boldsymbol{B}_{0}$
and a fluctuating magnetic field
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
. We assume that
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
. We assume that
![]() $\boldsymbol{E}=\unicode[STIX]{x1D6FF}\boldsymbol{E}$
; i.e. the average electric field is zero. Linear theory expresses
$\boldsymbol{E}=\unicode[STIX]{x1D6FF}\boldsymbol{E}$
; i.e. the average electric field is zero. Linear theory expresses
![]() $\unicode[STIX]{x1D6FF}f_{j}$
as a function of
$\unicode[STIX]{x1D6FF}f_{j}$
as a function of
![]() $f_{0j}$
and the electromagnetic field components.
$f_{0j}$
and the electromagnetic field components.
The distribution function
![]() $f_{j}$
in a collisionless plasma evolves according to the Vlasov equation,
$f_{j}$
in a collisionless plasma evolves according to the Vlasov equation,
where
![]() $q_{j}$
is the charge of a particle of species
$q_{j}$
is the charge of a particle of species
![]() $j$
,
$j$
,
![]() $c$
is the speed of light and
$c$
is the speed of light and
![]() $\boldsymbol{v}$
is the velocity coordinate. We assume that all fluctuating quantities behave like plane waves; i.e.
$\boldsymbol{v}$
is the velocity coordinate. We assume that all fluctuating quantities behave like plane waves; i.e.
![]() $\propto \exp (\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}-\text{i}\unicode[STIX]{x1D714}t)$
, where
$\propto \exp (\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}-\text{i}\unicode[STIX]{x1D714}t)$
, where
![]() $\boldsymbol{k}$
is the wave vector and
$\boldsymbol{k}$
is the wave vector and
![]() $\unicode[STIX]{x1D714}$
is the (complex) frequency. Linearising equation (2.2), using Faraday’s law and applying the method of characteristics, we obtain
$\unicode[STIX]{x1D714}$
is the (complex) frequency. Linearising equation (2.2), using Faraday’s law and applying the method of characteristics, we obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}f_{j} & = & \displaystyle -q_{j}\text{e}^{\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}-\text{i}\unicode[STIX]{x1D714}t}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D70F}\,\text{e}^{\text{i}\unicode[STIX]{x1D6FC}}\left\{E_{x}U\cos (\unicode[STIX]{x1D719}+\unicode[STIX]{x1D6FA}_{j}\unicode[STIX]{x1D70F})+E_{y}U\sin (\unicode[STIX]{x1D719}+\unicode[STIX]{x1D6FA}_{j}\unicode[STIX]{x1D70F})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,E_{z}\left[\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}p_{\Vert }}-V\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D717}+\unicode[STIX]{x1D6FA}_{j}\unicode[STIX]{x1D70F})\right]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF}f_{j} & = & \displaystyle -q_{j}\text{e}^{\text{i}\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}-\text{i}\unicode[STIX]{x1D714}t}\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D70F}\,\text{e}^{\text{i}\unicode[STIX]{x1D6FC}}\left\{E_{x}U\cos (\unicode[STIX]{x1D719}+\unicode[STIX]{x1D6FA}_{j}\unicode[STIX]{x1D70F})+E_{y}U\sin (\unicode[STIX]{x1D719}+\unicode[STIX]{x1D6FA}_{j}\unicode[STIX]{x1D70F})\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,E_{z}\left[\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}p_{\Vert }}-V\cos (\unicode[STIX]{x1D719}-\unicode[STIX]{x1D717}+\unicode[STIX]{x1D6FA}_{j}\unicode[STIX]{x1D70F})\right]\right\},\end{eqnarray}$$
where
![]() $\boldsymbol{E}=(E_{x},E_{y},E_{z})$
is the electric field,
$\boldsymbol{E}=(E_{x},E_{y},E_{z})$
is the electric field,
![]() $\unicode[STIX]{x1D719}$
is the azimuthal angle of the momentum vector
$\unicode[STIX]{x1D719}$
is the azimuthal angle of the momentum vector
![]() $\boldsymbol{p}$
,
$\boldsymbol{p}$
,
![]() $\unicode[STIX]{x1D717}$
is the azimuthal angle of the wave vector
$\unicode[STIX]{x1D717}$
is the azimuthal angle of the wave vector
![]() $\boldsymbol{k}$
, the index
$\boldsymbol{k}$
, the index
![]() $\bot$
(
$\bot$
(
![]() $\Vert$
) refers to the direction perpendicular (parallel) with respect to the background magnetic field
$\Vert$
) refers to the direction perpendicular (parallel) with respect to the background magnetic field
![]() $\boldsymbol{B}_{0}$
,
$\boldsymbol{B}_{0}$
,
is the relativistic gyrofrequency,
![]() $m_{j}$
is the rest mass of a particle of species
$m_{j}$
is the rest mass of a particle of species
![]() $j$
,
$j$
,
and
We normalise
![]() $f_{j}$
so that
$f_{j}$
so that
![]() $\int \text{d}^{3}\boldsymbol{p}\,f_{0j}=1$
. The first velocity moments of the distribution functions of all species define the current density
$\int \text{d}^{3}\boldsymbol{p}\,f_{0j}=1$
. The first velocity moments of the distribution functions of all species define the current density
![]() $\boldsymbol{j}$
through
$\boldsymbol{j}$
through
where
![]() $\unicode[STIX]{x1D74C}_{j}$
is the contribution of species
$\unicode[STIX]{x1D74C}_{j}$
is the contribution of species
![]() $j$
to the plasma susceptibility and
$j$
to the plasma susceptibility and
![]() $n_{0j}$
is the background density of species
$n_{0j}$
is the background density of species
![]() $j$
. Without loss of generality, we choose a cylindrical coordinate system in which
$j$
. Without loss of generality, we choose a cylindrical coordinate system in which
![]() $k_{y}=\unicode[STIX]{x1D717}=0$
and apply a set of Bessel-function identities in order to facilitate the integration over
$k_{y}=\unicode[STIX]{x1D717}=0$
and apply a set of Bessel-function identities in order to facilitate the integration over
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D70F}$
in (2.3). This allows us to rewrite the plasma susceptibilities as (provided that
$\unicode[STIX]{x1D70F}$
in (2.3). This allows us to rewrite the plasma susceptibilities as (provided that
![]() $\text{Im}(\unicode[STIX]{x1D714})>0$
)
$\text{Im}(\unicode[STIX]{x1D714})>0$
)
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D74C}_{j} & = & \displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}j}^{2}}{\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}_{0j}}\int _{0}^{\infty }2\unicode[STIX]{x03C0}p_{\bot }\,\text{d}p_{\bot }\int _{-\infty }^{+\infty }\text{d}p_{\Vert }\left[\hat{\boldsymbol{e}}_{\Vert }\hat{\boldsymbol{e}}_{\Vert }\frac{\unicode[STIX]{x1D6FA}_{j}}{\unicode[STIX]{x1D714}}\left(\frac{1}{p_{\Vert }}\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}p_{\Vert }}-\frac{1}{p_{\bot }}\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}p_{\bot }}\right)p_{\Vert }^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\mathop{\sum }_{n=-\infty }^{+\infty }\frac{\unicode[STIX]{x1D6FA}_{j}p_{\bot }U}{\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }-n\unicode[STIX]{x1D6FA}_{j}}\unicode[STIX]{x1D64F}_{n}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D74C}_{j} & = & \displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}j}^{2}}{\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}_{0j}}\int _{0}^{\infty }2\unicode[STIX]{x03C0}p_{\bot }\,\text{d}p_{\bot }\int _{-\infty }^{+\infty }\text{d}p_{\Vert }\left[\hat{\boldsymbol{e}}_{\Vert }\hat{\boldsymbol{e}}_{\Vert }\frac{\unicode[STIX]{x1D6FA}_{j}}{\unicode[STIX]{x1D714}}\left(\frac{1}{p_{\Vert }}\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}p_{\Vert }}-\frac{1}{p_{\bot }}\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}p_{\bot }}\right)p_{\Vert }^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\mathop{\sum }_{n=-\infty }^{+\infty }\frac{\unicode[STIX]{x1D6FA}_{j}p_{\bot }U}{\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }-n\unicode[STIX]{x1D6FA}_{j}}\unicode[STIX]{x1D64F}_{n}\right],\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D714}_{\text{p}j}\equiv \sqrt{4\unicode[STIX]{x03C0}n_{0j}q_{j}^{2}/m_{j}}$
is the plasma frequency of species
$\unicode[STIX]{x1D714}_{\text{p}j}\equiv \sqrt{4\unicode[STIX]{x03C0}n_{0j}q_{j}^{2}/m_{j}}$
is the plasma frequency of species
![]() $j$
,
$j$
,
![]() $\unicode[STIX]{x1D6FA}_{0j}\equiv q_{j}B_{0}/m_{j}c$
is the non-relativistic gyrofrequency and the tensor
$\unicode[STIX]{x1D6FA}_{0j}\equiv q_{j}B_{0}/m_{j}c$
is the non-relativistic gyrofrequency and the tensor
![]() $\unicode[STIX]{x1D64F}_{n}$
is defined as
$\unicode[STIX]{x1D64F}_{n}$
is defined as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64F}_{n}\equiv \left(\begin{array}{@{}ccc@{}}\displaystyle \frac{n^{2}\text{J}_{n}^{2}}{z^{2}} & \displaystyle \frac{\text{i}n\text{J}_{n}\text{J}_{n}^{\prime }}{z} & \displaystyle \frac{n\text{J}_{n}^{2}p_{\Vert }}{zp_{\bot }}\\ \displaystyle -\frac{\text{i}n\text{J}_{n}\text{J}_{n}^{\prime }}{z} & (\text{J}_{n}^{\prime })^{2} & \displaystyle -\frac{\text{i}\text{J}_{n}\text{J}_{n}^{\prime }p_{\Vert }}{p_{\bot }}\\ \displaystyle \frac{n\text{J}_{n}^{2}p_{\Vert }}{zp_{\bot }} & \displaystyle \frac{\text{i}\text{J}_{n}\text{J}_{n}^{\prime }p_{\Vert }}{p_{\bot }} & \displaystyle \frac{\text{J}_{n}^{2}p_{\Vert }^{2}}{p_{\bot }^{2}}\end{array}\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64F}_{n}\equiv \left(\begin{array}{@{}ccc@{}}\displaystyle \frac{n^{2}\text{J}_{n}^{2}}{z^{2}} & \displaystyle \frac{\text{i}n\text{J}_{n}\text{J}_{n}^{\prime }}{z} & \displaystyle \frac{n\text{J}_{n}^{2}p_{\Vert }}{zp_{\bot }}\\ \displaystyle -\frac{\text{i}n\text{J}_{n}\text{J}_{n}^{\prime }}{z} & (\text{J}_{n}^{\prime })^{2} & \displaystyle -\frac{\text{i}\text{J}_{n}\text{J}_{n}^{\prime }p_{\Vert }}{p_{\bot }}\\ \displaystyle \frac{n\text{J}_{n}^{2}p_{\Vert }}{zp_{\bot }} & \displaystyle \frac{\text{i}\text{J}_{n}\text{J}_{n}^{\prime }p_{\Vert }}{p_{\bot }} & \displaystyle \frac{\text{J}_{n}^{2}p_{\Vert }^{2}}{p_{\bot }^{2}}\end{array}\right), & & \displaystyle\end{eqnarray}$$
where
![]() $z\equiv k_{\bot }v_{\bot }/\unicode[STIX]{x1D6FA}_{j}$
and
$z\equiv k_{\bot }v_{\bot }/\unicode[STIX]{x1D6FA}_{j}$
and
![]() $\text{J}_{n}\equiv \text{J}_{n}(z)$
is the
$\text{J}_{n}\equiv \text{J}_{n}(z)$
is the
![]() $n$
th-order Bessel function. For
$n$
th-order Bessel function. For
![]() $\text{Im}(\unicode[STIX]{x1D714})\leqslant 0$
, the integral over
$\text{Im}(\unicode[STIX]{x1D714})\leqslant 0$
, the integral over
![]() $p_{\Vert }$
is executed as the Landau integral after analytic continuation (for details, see chapter 8 of Stix Reference Stix1992). Equation (2.9) describes the susceptibility for a general background distribution function
$p_{\Vert }$
is executed as the Landau integral after analytic continuation (for details, see chapter 8 of Stix Reference Stix1992). Equation (2.9) describes the susceptibility for a general background distribution function
![]() $f_{0j}$
in a relativistic plasma. The only assumptions are gyrotropy in
$f_{0j}$
in a relativistic plasma. The only assumptions are gyrotropy in
![]() $f_{0j}$
and small amplitudes in the fluctuations so that linearisation is applicable, and a uniform, stationary equilibrium. The numerical challenge in the solution of the plasma dispersion relation results from the integrals over
$f_{0j}$
and small amplitudes in the fluctuations so that linearisation is applicable, and a uniform, stationary equilibrium. The numerical challenge in the solution of the plasma dispersion relation results from the integrals over
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
in (2.9). We note that, in numerous classical codes for calculation of the linear hot-plasma dispersion relation (Roennmark Reference Roennmark1982; Gary Reference Gary1993; Klein & Howes Reference Klein and Howes2015; Verscharen & Chandran Reference Verscharen and Chandran2018), these integrals are greatly simplified by assuming that
$p_{\Vert }$
in (2.9). We note that, in numerous classical codes for calculation of the linear hot-plasma dispersion relation (Roennmark Reference Roennmark1982; Gary Reference Gary1993; Klein & Howes Reference Klein and Howes2015; Verscharen & Chandran Reference Verscharen and Chandran2018), these integrals are greatly simplified by assuming that
![]() $f_{0j}$
is a (bi)-Maxwellian.
$f_{0j}$
is a (bi)-Maxwellian.
The dielectric tensor
![]() $\unicode[STIX]{x1D73A}$
of the plasma is related to the plasma susceptibilities from (2.9) through
$\unicode[STIX]{x1D73A}$
of the plasma is related to the plasma susceptibilities from (2.9) through
Finally, combining Faraday’s law and Ampère’s law leads to the wave equation,
where
![]() $\boldsymbol{n}_{\text{r}}\equiv \boldsymbol{k}c/\unicode[STIX]{x1D714}$
is the refractive index. By setting
$\boldsymbol{n}_{\text{r}}\equiv \boldsymbol{k}c/\unicode[STIX]{x1D714}$
is the refractive index. By setting
![]() $\text{det}\,{\mathcal{D}}=0$
, we obtain the dispersion relations
$\text{det}\,{\mathcal{D}}=0$
, we obtain the dispersion relations
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}(\boldsymbol{k})$
for non-trivial solutions to (2.12). We write these solutions in the form
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}(\boldsymbol{k})$
for non-trivial solutions to (2.12). We write these solutions in the form
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{r}}+\text{i}\unicode[STIX]{x1D6FE}$
, where
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{r}}+\text{i}\unicode[STIX]{x1D6FE}$
, where
![]() $\unicode[STIX]{x1D714}_{\text{r}}=\text{Re}(\unicode[STIX]{x1D714})$
and
$\unicode[STIX]{x1D714}_{\text{r}}=\text{Re}(\unicode[STIX]{x1D714})$
and
![]() $\unicode[STIX]{x1D6FE}=\text{Im}(\unicode[STIX]{x1D714})$
.
$\unicode[STIX]{x1D6FE}=\text{Im}(\unicode[STIX]{x1D714})$
.
3 Numerical approach
In order to find the solutions to the hot-plasma dispersion relation, ALPS determines the values of
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}$
and
![]() $\unicode[STIX]{x1D6FE}$
that solve (2.12) for specified background distributions
$\unicode[STIX]{x1D6FE}$
that solve (2.12) for specified background distributions
![]() $f_{0j}$
at a given set of values for
$f_{0j}$
at a given set of values for
![]() $\boldsymbol{k}$
,
$\boldsymbol{k}$
,
![]() $m_{j}$
,
$m_{j}$
,
![]() $q_{j}$
,
$q_{j}$
,
![]() $n_{0j}$
and
$n_{0j}$
and
![]() $v_{\text{A}}/c$
, where
$v_{\text{A}}/c$
, where
![]() $v_{\text{A}}\equiv B_{0}/\sqrt{4\unicode[STIX]{x03C0}n_{0\text{p}}m_{\text{p}}}$
. ALPS uses an efficient iterative Newton-secant algorithm to solve (2.12) based on an initial guess for
$v_{\text{A}}\equiv B_{0}/\sqrt{4\unicode[STIX]{x03C0}n_{0\text{p}}m_{\text{p}}}$
. ALPS uses an efficient iterative Newton-secant algorithm to solve (2.12) based on an initial guess for
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}$
and
![]() $\unicode[STIX]{x1D6FE}$
(Press et al.
Reference Press, Teukolsky, Vetterling and Flannery1992). The numerically challenging part for this calculation is the evaluation of
$\unicode[STIX]{x1D6FE}$
(Press et al.
Reference Press, Teukolsky, Vetterling and Flannery1992). The numerically challenging part for this calculation is the evaluation of
![]() $\unicode[STIX]{x1D74C}_{j}$
in (2.9). In the following, we present ALPS’s strategy for this evaluation in the non-relativistic case. We discuss the extension to relativistic cases with poles in the integration domain in § 3.3, which is equivalent to the non-relativistic case with the exception that the coordinate system is transformed from
$\unicode[STIX]{x1D74C}_{j}$
in (2.9). In the following, we present ALPS’s strategy for this evaluation in the non-relativistic case. We discuss the extension to relativistic cases with poles in the integration domain in § 3.3, which is equivalent to the non-relativistic case with the exception that the coordinate system is transformed from
![]() $(p_{\bot },p_{\Vert })$
to
$(p_{\bot },p_{\Vert })$
to
![]() $(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
, where
$(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
, where
![]() $\unicode[STIX]{x1D6E4}$
is the Lorentz factor and
$\unicode[STIX]{x1D6E4}$
is the Lorentz factor and
![]() $\bar{p}_{\Vert }\equiv p_{\Vert }/m_{j}c$
, and that (3.16) below is used instead of (2.9).
$\bar{p}_{\Vert }\equiv p_{\Vert }/m_{j}c$
, and that (3.16) below is used instead of (2.9).
We prescribe the shape of
![]() $f_{0j}$
in input files for each species (called ‘
$f_{0j}$
in input files for each species (called ‘
![]() $f_{0}$
table’) as an ASCII table that lists
$f_{0}$
table’) as an ASCII table that lists
![]() $p_{\bot }$
,
$p_{\bot }$
,
![]() $p_{\Vert }$
and the associated values of
$p_{\Vert }$
and the associated values of
![]() $f_{0j}$
. From this table, we calculate
$f_{0j}$
. From this table, we calculate
![]() $\unicode[STIX]{x2202}f_{0j}/\unicode[STIX]{x2202}p_{\bot }$
and
$\unicode[STIX]{x2202}f_{0j}/\unicode[STIX]{x2202}p_{\bot }$
and
![]() $\unicode[STIX]{x2202}f_{0j}/\unicode[STIX]{x2202}p_{\Vert }$
on the same grid as the
$\unicode[STIX]{x2202}f_{0j}/\unicode[STIX]{x2202}p_{\Vert }$
on the same grid as the
![]() $f_{0}$
table using second-order finite differencing. We do not include the derivatives at the outer boundaries of the (
$f_{0}$
table using second-order finite differencing. We do not include the derivatives at the outer boundaries of the (
![]() $p_{\bot }$
,
$p_{\bot }$
,
![]() $p_{\Vert }$
) domain. The resolution of the
$p_{\Vert }$
) domain. The resolution of the
![]() $f_{0}$
table is given by
$f_{0}$
table is given by
![]() $N_{\bot }$
points in the
$N_{\bot }$
points in the
![]() $p_{\bot }$
-direction and
$p_{\bot }$
-direction and
![]() $N_{\Vert }$
points in the
$N_{\Vert }$
points in the
![]() $p_{\Vert }$
-direction. The table spans from
$p_{\Vert }$
-direction. The table spans from
![]() $p_{\bot }=0$
to
$p_{\bot }=0$
to
![]() $p_{\bot }=P_{\max ,\bot j}$
in the perpendicular direction and from
$p_{\bot }=P_{\max ,\bot j}$
in the perpendicular direction and from
![]() $p_{\Vert }=-P_{\max ,\Vert j}$
to
$p_{\Vert }=-P_{\max ,\Vert j}$
to
![]() $p_{\Vert }=P_{\max ,\Vert j}$
in the parallel direction.
$p_{\Vert }=P_{\max ,\Vert j}$
in the parallel direction.
The integration in (2.9) allows us to integrate separately and independently for each
![]() $n$
and
$n$
and
![]() $j$
. This provides us with a very natural way to parallelise the calculation scheme by assigning the separate integrations to different processors. We use MPI for the parallelisation. The integrating nodes return their contributions to
$j$
. This provides us with a very natural way to parallelise the calculation scheme by assigning the separate integrations to different processors. We use MPI for the parallelisation. The integrating nodes return their contributions to
![]() $\unicode[STIX]{x1D74C}_{j}$
to the master node, which then sums up the contributions, determines the value of
$\unicode[STIX]{x1D74C}_{j}$
to the master node, which then sums up the contributions, determines the value of
![]() $\unicode[STIX]{x1D73A}$
and updates the values of
$\unicode[STIX]{x1D73A}$
and updates the values of
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}$
and
![]() $\unicode[STIX]{x1D6FE}$
through a Newton-secant step. The updated values for
$\unicode[STIX]{x1D6FE}$
through a Newton-secant step. The updated values for
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}$
and
![]() $\unicode[STIX]{x1D6FE}$
are then returned to the integrating nodes, which afterwards evaluate the integration of their updated contribution to
$\unicode[STIX]{x1D6FE}$
are then returned to the integrating nodes, which afterwards evaluate the integration of their updated contribution to
![]() $\unicode[STIX]{x1D74C}_{j}$
. We evaluate all values of
$\unicode[STIX]{x1D74C}_{j}$
. We evaluate all values of
![]() $n$
up to a value of
$n$
up to a value of
![]() $\pm n_{\max }$
, which is determined as the value of
$\pm n_{\max }$
, which is determined as the value of
![]() $n$
for which the maximum value of
$n$
for which the maximum value of
![]() $|\text{J}_{n}|$
is smaller than the user-defined parameter
$|\text{J}_{n}|$
is smaller than the user-defined parameter
![]() $J_{\max }$
. The necessary value of
$J_{\max }$
. The necessary value of
![]() $n_{\max }$
depends on the wavenumber, the direction of propagation of the treated wave and the thermal speeds of the plasma components. In bi-Maxwellian codes under typical solar-wind conditions, the accuracy of the dispersion relation is better than
$n_{\max }$
depends on the wavenumber, the direction of propagation of the treated wave and the thermal speeds of the plasma components. In bi-Maxwellian codes under typical solar-wind conditions, the accuracy of the dispersion relation is better than
![]() $\unicode[STIX]{x0394}|\unicode[STIX]{x1D714}|/|\unicode[STIX]{x1D714}|\sim 10^{-5}$
for
$\unicode[STIX]{x0394}|\unicode[STIX]{x1D714}|/|\unicode[STIX]{x1D714}|\sim 10^{-5}$
for
![]() $J_{\max }\sim 10^{-45}$
(which typically corresponds to
$J_{\max }\sim 10^{-45}$
(which typically corresponds to
![]() $n_{\max }\gtrsim 10$
at proton scales).
$n_{\max }\gtrsim 10$
at proton scales).
We use a standard two-dimensional trapezoidal integration scheme to integrate over
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
. However, this scheme breaks down near the poles of the integrand in (2.9) and requires a special treatment of the analytic continuation when
$p_{\Vert }$
. However, this scheme breaks down near the poles of the integrand in (2.9) and requires a special treatment of the analytic continuation when
![]() $\unicode[STIX]{x1D6FE}\leqslant 0$
. In the remainder of this section, we discuss our strategies to resolve these numerical difficulties.
$\unicode[STIX]{x1D6FE}\leqslant 0$
. In the remainder of this section, we discuss our strategies to resolve these numerical difficulties.
3.1 Integrating near poles
A challenge concerning the numerical integration is the treatment of the poles that occur in the term proportional to
![]() $\unicode[STIX]{x1D64F}_{n}$
in (2.9). The integrals in question are of the form
$\unicode[STIX]{x1D64F}_{n}$
in (2.9). The integrals in question are of the form
for
![]() $\unicode[STIX]{x1D6FE}>0$
. For sufficiently small
$\unicode[STIX]{x1D6FE}>0$
. For sufficiently small
![]() $\unicode[STIX]{x1D6FE}$
, the denominator in (3.1) can become very small along the real
$\unicode[STIX]{x1D6FE}$
, the denominator in (3.1) can become very small along the real
![]() $p_{\Vert }$
axis so that the grid sampling leads to large numerical errors in the integration. To describe how we evaluate these integrals, we first rewrite the integral in (3.1) in the more generic form
$p_{\Vert }$
axis so that the grid sampling leads to large numerical errors in the integration. To describe how we evaluate these integrals, we first rewrite the integral in (3.1) in the more generic form
where
![]() $x$
,
$x$
,
![]() $t_{\text{r}}$
and
$t_{\text{r}}$
and
![]() $t_{\text{i}}$
are real,
$t_{\text{i}}$
are real,
![]() $g(x)$
is a smooth function and the integration is performed along the real axis. We choose a symmetric interval
$g(x)$
is a smooth function and the integration is performed along the real axis. We choose a symmetric interval
![]() $[t_{\text{r}}-\unicode[STIX]{x1D6E5},t_{\text{r}}+\unicode[STIX]{x1D6E5}]$
around
$[t_{\text{r}}-\unicode[STIX]{x1D6E5},t_{\text{r}}+\unicode[STIX]{x1D6E5}]$
around
![]() $t_{\text{r}}$
where
$t_{\text{r}}$
where
![]() $\unicode[STIX]{x1D6E5}\ll g(t_{\text{r}})/g^{\prime }(t_{\text{r}})$
, and write
$\unicode[STIX]{x1D6E5}\ll g(t_{\text{r}})/g^{\prime }(t_{\text{r}})$
, and write
where ‘rest’ refers to the integration outside the interval
![]() $[t_{\text{r}}-\unicode[STIX]{x1D6E5},t_{\text{r}}+\unicode[STIX]{x1D6E5}]$
. We define a function
$[t_{\text{r}}-\unicode[STIX]{x1D6E5},t_{\text{r}}+\unicode[STIX]{x1D6E5}]$
. We define a function
![]() $f(x)$
to be odd with respect to
$f(x)$
to be odd with respect to
![]() $t_{\text{r}}$
if
$t_{\text{r}}$
if
![]() $f(x)=-f(2t_{\text{r}}-x)$
, and even with respect to
$f(x)=-f(2t_{\text{r}}-x)$
, and even with respect to
![]() $t_{\text{r}}$
if
$t_{\text{r}}$
if
![]() $f(x)=f(2t_{\text{r}}-x)$
. Following Longman (Reference Longman1958) and Davis & Rabinowitz (Reference Davis and Rabinowitz1984), we then separate the integrand into its odd and even parts with respect to
$f(x)=f(2t_{\text{r}}-x)$
. Following Longman (Reference Longman1958) and Davis & Rabinowitz (Reference Davis and Rabinowitz1984), we then separate the integrand into its odd and even parts with respect to
![]() $t_{\text{r}}$
as
$t_{\text{r}}$
as
 $$\begin{eqnarray}\displaystyle {\mathcal{I}} & = & \displaystyle \frac{1}{2}\int _{t_{\text{r}}-\unicode[STIX]{x1D6E5}}^{t_{\text{r}}+\unicode[STIX]{x1D6E5}}\text{d}x\left[\frac{g(x)}{x-t_{\text{r}}-\text{i}t_{\text{i}}}-\frac{g(2t_{\text{r}}-x)}{-x+t_{\text{r}}-\text{i}t_{\text{i}}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\int _{t_{\text{r}}-\unicode[STIX]{x1D6E5}}^{t_{\text{r}}+\unicode[STIX]{x1D6E5}}\text{d}x\left[\frac{g(x)}{x-t_{\text{r}}-\text{i}t_{\text{i}}}+\frac{g(2t_{\text{r}}-x)}{-x+t_{\text{r}}-\text{i}t_{\text{i}}}\right]+\text{rest}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{I}} & = & \displaystyle \frac{1}{2}\int _{t_{\text{r}}-\unicode[STIX]{x1D6E5}}^{t_{\text{r}}+\unicode[STIX]{x1D6E5}}\text{d}x\left[\frac{g(x)}{x-t_{\text{r}}-\text{i}t_{\text{i}}}-\frac{g(2t_{\text{r}}-x)}{-x+t_{\text{r}}-\text{i}t_{\text{i}}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}\int _{t_{\text{r}}-\unicode[STIX]{x1D6E5}}^{t_{\text{r}}+\unicode[STIX]{x1D6E5}}\text{d}x\left[\frac{g(x)}{x-t_{\text{r}}-\text{i}t_{\text{i}}}+\frac{g(2t_{\text{r}}-x)}{-x+t_{\text{r}}-\text{i}t_{\text{i}}}\right]+\text{rest}.\end{eqnarray}$$
The integrand in the first integral in (3.4) is odd with respect to
![]() $t_{\text{r}}$
and thus vanishes after the integration over the symmetric interval around
$t_{\text{r}}$
and thus vanishes after the integration over the symmetric interval around
![]() $t_{\text{r}}$
. The second integral, on the other hand, is even with respect to
$t_{\text{r}}$
. The second integral, on the other hand, is even with respect to
![]() $t_{\text{r}}$
and thus
$t_{\text{r}}$
and thus
We define
![]() $\unicode[STIX]{x1D6E5}$
through a user-defined parameter
$\unicode[STIX]{x1D6E5}$
through a user-defined parameter
![]() $M_{\text{I}}$
so that
$M_{\text{I}}$
so that
![]() $\unicode[STIX]{x1D6E5}\equiv M_{\text{I}}\,\unicode[STIX]{x0394}p_{\Vert }$
, where
$\unicode[STIX]{x1D6E5}\equiv M_{\text{I}}\,\unicode[STIX]{x0394}p_{\Vert }$
, where
![]() $\unicode[STIX]{x0394}p_{\Vert }$
is the size of a grid step in the parallel direction. We then define
$\unicode[STIX]{x0394}p_{\Vert }$
is the size of a grid step in the parallel direction. We then define
![]() $\unicode[STIX]{x1D6FF}\equiv \unicode[STIX]{x1D6E5}/M_{\text{P}}$
, where
$\unicode[STIX]{x1D6FF}\equiv \unicode[STIX]{x1D6E5}/M_{\text{P}}$
, where
![]() $M_{\text{P}}$
is another user-defined parameter. Except for cases in which
$M_{\text{P}}$
is another user-defined parameter. Except for cases in which
![]() $|t_{\text{i}}|$
is extremely small, we apply a trapezoidal integration over
$|t_{\text{i}}|$
is extremely small, we apply a trapezoidal integration over
![]() $M_{\text{P}}$
steps of width
$M_{\text{P}}$
steps of width
![]() $\unicode[STIX]{x1D6FF}$
to the integral in (3.5). The smoothness of
$\unicode[STIX]{x1D6FF}$
to the integral in (3.5). The smoothness of
![]() $g(x)$
allows us to expand
$g(x)$
allows us to expand
![]() $g(x)$
around the nearest grid point of the
$g(x)$
around the nearest grid point of the
![]() $M_{\text{I}}$
grid points in the interval
$M_{\text{I}}$
grid points in the interval
![]() $[t_{\text{r}},t_{\text{r}}+\unicode[STIX]{x1D6E5}]$
using a Taylor series. By taking
$[t_{\text{r}},t_{\text{r}}+\unicode[STIX]{x1D6E5}]$
using a Taylor series. By taking
![]() $\unicode[STIX]{x0394}p_{\Vert }$
to be sufficiently small, we can retain just the first two terms in the series without losing significant accuracy. Since the integral in (3.5) does not converge numerically if
$\unicode[STIX]{x0394}p_{\Vert }$
to be sufficiently small, we can retain just the first two terms in the series without losing significant accuracy. Since the integral in (3.5) does not converge numerically if
![]() $|t_{\text{i}}|$
is extremely small, we implement the following procedure when
$|t_{\text{i}}|$
is extremely small, we implement the following procedure when
![]() $|t_{\text{i}}|\leqslant t_{\text{lim}}$
, where
$|t_{\text{i}}|\leqslant t_{\text{lim}}$
, where
![]() $t_{\text{lim}}$
is a user-defined parameter. We first rewrite (3.5) using truncated Taylor expansions of
$t_{\text{lim}}$
is a user-defined parameter. We first rewrite (3.5) using truncated Taylor expansions of
![]() $g(x)$
and
$g(x)$
and
![]() $g(2t_{\text{r}}-x)$
around
$g(2t_{\text{r}}-x)$
around
![]() $x=t_{\text{r}}$
as
$x=t_{\text{r}}$
as
We determine
![]() $g(t_{\text{r}})$
and
$g(t_{\text{r}})$
and
![]() $g^{\prime }(t_{\text{r}})$
through linear interpolation between the neighbouring grid points to
$g^{\prime }(t_{\text{r}})$
through linear interpolation between the neighbouring grid points to
![]() $t_{\text{r}}$
. The term proportional to
$t_{\text{r}}$
. The term proportional to
![]() $g^{\prime }(t_{\text{r}})$
in (3.6) converges numerically for any value of
$g^{\prime }(t_{\text{r}})$
in (3.6) converges numerically for any value of
![]() $t_{\text{i}}$
. We set the term proportional to
$t_{\text{i}}$
. We set the term proportional to
![]() $g(t_{\text{r}})$
equal to its small-
$g(t_{\text{r}})$
equal to its small-
![]() $t_{\text{i}}$
limit, namely
$t_{\text{i}}$
limit, namely
We use this method for both the integration of
![]() $\unicode[STIX]{x1D74C}_{j}$
near poles and the principal-value integration that is necessary if
$\unicode[STIX]{x1D74C}_{j}$
near poles and the principal-value integration that is necessary if
![]() $\unicode[STIX]{x1D6FE}=0$
.
$\unicode[STIX]{x1D6FE}=0$
.
3.2 Analytic continuation
If
![]() $\unicode[STIX]{x1D6FE}\leqslant 0$
, the integration in (2.9) requires an analytic continuation into the complex plane. If
$\unicode[STIX]{x1D6FE}\leqslant 0$
, the integration in (2.9) requires an analytic continuation into the complex plane. If
![]() $f_{0j}$
were given as a closed algebraic expression, the analytic continuation would simply entail the evaluation of
$f_{0j}$
were given as a closed algebraic expression, the analytic continuation would simply entail the evaluation of
![]() $f_{0j}(p_{\bot },p_{\Vert })$
at a complex value for
$f_{0j}(p_{\bot },p_{\Vert })$
at a complex value for
![]() $p_{\Vert }$
in the non-relativistic case. In our case, however,
$p_{\Vert }$
in the non-relativistic case. In our case, however,
![]() $f_{0j}$
is only defined on a real grid in
$f_{0j}$
is only defined on a real grid in
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
, yet the analytic continuation of
$p_{\Vert }$
, yet the analytic continuation of
![]() $f_{0j}$
is still uniquely defined. This leads to the known mathematical problem of numerical analytic continuation (Cannon & Miller Reference Cannon and Miller1965; Reichel Reference Reichel1986; Fujiwara et al.
Reference Fujiwara, Imai, Takeuchi and Iso2007; Fu et al.
Reference Fu, Zhang, Cheng and Ma2012; Zhang & Ma Reference Zhang and Ma2013; Kranich Reference Kranich2014). Our solution for this problem is our hybrid analytic continuation scheme. We note that this approach is only relevant for damped modes, i.e.
$f_{0j}$
is still uniquely defined. This leads to the known mathematical problem of numerical analytic continuation (Cannon & Miller Reference Cannon and Miller1965; Reichel Reference Reichel1986; Fujiwara et al.
Reference Fujiwara, Imai, Takeuchi and Iso2007; Fu et al.
Reference Fu, Zhang, Cheng and Ma2012; Zhang & Ma Reference Zhang and Ma2013; Kranich Reference Kranich2014). Our solution for this problem is our hybrid analytic continuation scheme. We note that this approach is only relevant for damped modes, i.e.
![]() $\unicode[STIX]{x1D6FE}\leqslant 0$
.
$\unicode[STIX]{x1D6FE}\leqslant 0$
.
Landau’s rule of integration around singularities (Landau Reference Landau1946; Lifshitz & Pitaevskii Reference Lifshitz and Pitaevskii1981) leads to the following three cases with the appropriate residues for the evaluation of
![]() $I(p_{\bot })$
for general
$I(p_{\bot })$
for general
![]() $\unicode[STIX]{x1D6FE}$
:
$\unicode[STIX]{x1D6FE}$
:
 $$\begin{eqnarray}\displaystyle I(p_{\bot })=\int _{C_{\text{L}}}\text{d}p_{\Vert }G(p_{\bot },p_{\Vert })=\left\{\begin{array}{@{}ll@{}}\displaystyle \int _{-\infty }^{+\infty }\text{d}p_{\Vert }G(p_{\bot },p_{\Vert })\quad & \text{if }\unicode[STIX]{x1D6FE}>0,\\ \displaystyle {\mathcal{P}}\int _{-\infty }^{+\infty }\text{d}p_{\Vert }G(p_{\bot },p_{\Vert })+\text{i}\unicode[STIX]{x03C0}\sum \text{Res}_{A}(G)\quad & \text{if }\unicode[STIX]{x1D6FE}=0,\\ \displaystyle \int _{-\infty }^{+\infty }\text{d}p_{\Vert }G(p_{\bot },p_{\Vert })+2\text{i}\unicode[STIX]{x03C0}\sum \text{Res}_{A}(G)\quad & \text{if }\unicode[STIX]{x1D6FE}<0,\end{array}\right. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I(p_{\bot })=\int _{C_{\text{L}}}\text{d}p_{\Vert }G(p_{\bot },p_{\Vert })=\left\{\begin{array}{@{}ll@{}}\displaystyle \int _{-\infty }^{+\infty }\text{d}p_{\Vert }G(p_{\bot },p_{\Vert })\quad & \text{if }\unicode[STIX]{x1D6FE}>0,\\ \displaystyle {\mathcal{P}}\int _{-\infty }^{+\infty }\text{d}p_{\Vert }G(p_{\bot },p_{\Vert })+\text{i}\unicode[STIX]{x03C0}\sum \text{Res}_{A}(G)\quad & \text{if }\unicode[STIX]{x1D6FE}=0,\\ \displaystyle \int _{-\infty }^{+\infty }\text{d}p_{\Vert }G(p_{\bot },p_{\Vert })+2\text{i}\unicode[STIX]{x03C0}\sum \text{Res}_{A}(G)\quad & \text{if }\unicode[STIX]{x1D6FE}<0,\end{array}\right. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
![]() $C_{\text{L}}$
is the contour of the Landau integration, which lies below the complex poles in the integrand. The integrations on the right-hand side of (3.8) are performed along the real axis, and
$C_{\text{L}}$
is the contour of the Landau integration, which lies below the complex poles in the integrand. The integrations on the right-hand side of (3.8) are performed along the real axis, and
![]() ${\mathcal{P}}$
indicates the principal-value integral. The sum sign indicates the summation over the residues of all poles
${\mathcal{P}}$
indicates the principal-value integral. The sum sign indicates the summation over the residues of all poles
![]() $A$
of the function
$A$
of the function
![]() $G$
. In a non-relativistic plasma,
$G$
. In a non-relativistic plasma,
![]() $G$
has one simple pole, and thus
$G$
has one simple pole, and thus
where
![]() $p_{\text{pole}}=m_{j}(\unicode[STIX]{x1D714}-n\unicode[STIX]{x1D6FA}_{j})/k_{\Vert }$
is the parallel momentum associated with pole
$p_{\text{pole}}=m_{j}(\unicode[STIX]{x1D714}-n\unicode[STIX]{x1D6FA}_{j})/k_{\Vert }$
is the parallel momentum associated with pole
![]() $A$
.
$A$
.
It is a common approach to decompose the background distribution functions in terms of analytical expressions and then to evaluate these at the complex poles. Complete orthogonal basis functions such as Hermite, Legendre or Chebyshev polynomials are the prime candidates for such a decomposition since they can represent
![]() $f_{0j}$
to an arbitrary degree of accuracy (Robinson Reference Robinson1990; Weideman Reference Weideman1995; Xie Reference Xie2013). These approaches are useful when
$f_{0j}$
to an arbitrary degree of accuracy (Robinson Reference Robinson1990; Weideman Reference Weideman1995; Xie Reference Xie2013). These approaches are useful when
![]() $f_{0j}$
deviates only slightly from a Maxwellian. They require, however, very high orders of decomposition and are thus slow in the presence of typical structures that we see in the solar wind such as a proton core–beam configuration. Therefore, they are unsuitable for ALPS’s purpose, and we pursue a different approach, which we call the hybrid analytic continuation. The basic idea behind this approach is to integrate
$f_{0j}$
deviates only slightly from a Maxwellian. They require, however, very high orders of decomposition and are thus slow in the presence of typical structures that we see in the solar wind such as a proton core–beam configuration. Therefore, they are unsuitable for ALPS’s purpose, and we pursue a different approach, which we call the hybrid analytic continuation. The basic idea behind this approach is to integrate
![]() $I$
numerically along the real axis whenever possible and to resort to an algebraic function for the sole purpose of the evaluation of
$I$
numerically along the real axis whenever possible and to resort to an algebraic function for the sole purpose of the evaluation of
![]() $\text{Res}_{A}(G)$
when necessary.
$\text{Res}_{A}(G)$
when necessary.
For the determination of an appropriate algebraic function, ALPS allows the user to choose an arbitrary combination of fit functions to represent
![]() $f_{0j}$
and automatically evaluates the fits before the integration begins. The code evaluates the fits separately at each
$f_{0j}$
and automatically evaluates the fits before the integration begins. The code evaluates the fits separately at each
![]() $p_{\bot }$
, so that no assumption is made as to the structure of
$p_{\bot }$
, so that no assumption is made as to the structure of
![]() $f_{0j}$
in the
$f_{0j}$
in the
![]() $p_{\bot }$
-direction. ALPS uses these functions only if a pole is within the integration domain and only if
$p_{\bot }$
-direction. ALPS uses these functions only if a pole is within the integration domain and only if
![]() $\unicode[STIX]{x1D6FE}\leqslant 0$
. The intrinsic fit functions that the code can combine include a Maxwellian distribution,
$\unicode[STIX]{x1D6FE}\leqslant 0$
. The intrinsic fit functions that the code can combine include a Maxwellian distribution,
where
![]() $w_{\bot j}\equiv \sqrt{2k_{\text{B}}T_{\bot j}/m_{j}}$
(
$w_{\bot j}\equiv \sqrt{2k_{\text{B}}T_{\bot j}/m_{j}}$
(
![]() $w_{\Vert j}\equiv \sqrt{2k_{\text{B}}T_{\Vert j}/m_{j}}$
) is the thermal speed of species
$w_{\Vert j}\equiv \sqrt{2k_{\text{B}}T_{\Vert j}/m_{j}}$
) is the thermal speed of species
![]() $j$
in the direction perpendicular (parallel) with respect to
$j$
in the direction perpendicular (parallel) with respect to
![]() $\boldsymbol{B}_{0}$
,
$\boldsymbol{B}_{0}$
,
![]() $T_{\bot j}$
(
$T_{\bot j}$
(
![]() $T_{\Vert j}$
) is the temperature of species
$T_{\Vert j}$
) is the temperature of species
![]() $j$
perpendicular (parallel) to
$j$
perpendicular (parallel) to
![]() $\boldsymbol{B}_{0}$
,
$\boldsymbol{B}_{0}$
,
![]() $k_{\text{B}}$
is the Boltzmann constant and
$k_{\text{B}}$
is the Boltzmann constant and
![]() $U_{j}$
is the
$U_{j}$
is the
![]() $\boldsymbol{B}_{0}$
-parallel drift speed of species
$\boldsymbol{B}_{0}$
-parallel drift speed of species
![]() $j$
; a
$j$
; a
![]() $\unicode[STIX]{x1D705}$
-distribution (Summers et al.
Reference Summers, Xue and Thorne1994; Astfalk, Görler & Jenko Reference Astfalk, Görler and Jenko2015),
$\unicode[STIX]{x1D705}$
-distribution (Summers et al.
Reference Summers, Xue and Thorne1994; Astfalk, Görler & Jenko Reference Astfalk, Görler and Jenko2015),
 $$\begin{eqnarray}\displaystyle f_{0j} & = & \displaystyle \frac{1}{m_{j}^{3}w_{\bot j}^{2}w_{\Vert j}}\left[\frac{2}{\unicode[STIX]{x03C0}(2\unicode[STIX]{x1D705}-3)}\right]^{3/2}\frac{\tilde{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D705}+1)}{\tilde{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D705}-1/2)}\nonumber\\ \displaystyle & & \displaystyle \times \left\{1+\frac{2}{2\unicode[STIX]{x1D705}-3}\left[\frac{p_{\bot }^{2}}{m_{j}^{2}w_{\bot j}^{2}}+\frac{(p_{\Vert }-m_{j}U_{j})^{2}}{m_{j}^{2}w_{\Vert j}^{2}}\right]\right\}^{-(\unicode[STIX]{x1D705}+1)};\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{0j} & = & \displaystyle \frac{1}{m_{j}^{3}w_{\bot j}^{2}w_{\Vert j}}\left[\frac{2}{\unicode[STIX]{x03C0}(2\unicode[STIX]{x1D705}-3)}\right]^{3/2}\frac{\tilde{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D705}+1)}{\tilde{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D705}-1/2)}\nonumber\\ \displaystyle & & \displaystyle \times \left\{1+\frac{2}{2\unicode[STIX]{x1D705}-3}\left[\frac{p_{\bot }^{2}}{m_{j}^{2}w_{\bot j}^{2}}+\frac{(p_{\Vert }-m_{j}U_{j})^{2}}{m_{j}^{2}w_{\Vert j}^{2}}\right]\right\}^{-(\unicode[STIX]{x1D705}+1)};\end{eqnarray}$$
and a Jüttner distribution (Jüttner Reference Jüttner1911; Chacón-Acosta, Dagdug & Morales-Técotl Reference Chacón-Acosta, Dagdug and Morales-Técotl2010),
where
![]() $\unicode[STIX]{x1D705}$
is the
$\unicode[STIX]{x1D705}$
is the
![]() $\unicode[STIX]{x1D705}$
-index and
$\unicode[STIX]{x1D705}$
-index and
![]() $\text{K}_{2}$
is the modified Bessel function of the second kind. The Jüttner distribution is the thermodynamic equilibrium distribution if
$\text{K}_{2}$
is the modified Bessel function of the second kind. The Jüttner distribution is the thermodynamic equilibrium distribution if
![]() $k_{\text{B}}T_{j}\gtrsim m_{j}c^{2}$
. The exponential in (3.12) reduces to the Maxwellian
$k_{\text{B}}T_{j}\gtrsim m_{j}c^{2}$
. The exponential in (3.12) reduces to the Maxwellian
![]() $\exp (-v^{2}/w_{j}^{2})$
with a different
$\exp (-v^{2}/w_{j}^{2})$
with a different
![]() $\boldsymbol{p}$
-independent normalisation factor for
$\boldsymbol{p}$
-independent normalisation factor for
![]() $p^{2}/m_{j}^{2}c^{2}\ll 1$
. We use an automated Levenberg–Marquardt-fit algorithm (Levenberg Reference Levenberg1944; Marquardt Reference Marquardt1963) and describe the details of the fit routine in appendix B.
$p^{2}/m_{j}^{2}c^{2}\ll 1$
. We use an automated Levenberg–Marquardt-fit algorithm (Levenberg Reference Levenberg1944; Marquardt Reference Marquardt1963) and describe the details of the fit routine in appendix B.
3.3 The poles in a relativistic plasma
The analytic continuation and pole handling in the relativistic case entail a further complication due to the non-trivial
![]() $\boldsymbol{p}$
-dependence of the resonant denominator in (2.9) (Buti Reference Buti1962; Lerche Reference Lerche1968). We define a plasma to be relativistic when there is a significant number of particles at relativistic velocities. This can be the case in plasmas with relativistic temperatures (
$\boldsymbol{p}$
-dependence of the resonant denominator in (2.9) (Buti Reference Buti1962; Lerche Reference Lerche1968). We define a plasma to be relativistic when there is a significant number of particles at relativistic velocities. This can be the case in plasmas with relativistic temperatures (
![]() $k_{\text{B}}T_{j}\gtrsim m_{j}c^{2}$
) or in plasmas with relativistic beams (
$k_{\text{B}}T_{j}\gtrsim m_{j}c^{2}$
) or in plasmas with relativistic beams (
![]() $P_{j}\gtrsim m_{j}c$
, where
$P_{j}\gtrsim m_{j}c$
, where
![]() $P_{j}$
is the drift momentum). Using the relativistic expression for
$P_{j}$
is the drift momentum). Using the relativistic expression for
![]() $\unicode[STIX]{x1D6FA}_{j}$
in (2.4) shows that we can write for the pole of the function under the integral sign in (3.1)
$\unicode[STIX]{x1D6FA}_{j}$
in (2.4) shows that we can write for the pole of the function under the integral sign in (3.1)
 $$\begin{eqnarray}\displaystyle \frac{1}{\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }-n\unicode[STIX]{x1D6FA}_{j}}=-\frac{1}{k_{\Vert }}\frac{\unicode[STIX]{x1D6E4}m_{j}}{\displaystyle \left(p_{\Vert }-\frac{\unicode[STIX]{x1D714}}{k_{\Vert }}\unicode[STIX]{x1D6E4}m_{j}+n\frac{\unicode[STIX]{x1D6FA}_{0j}}{k_{\Vert }}m_{j}\right)}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }-n\unicode[STIX]{x1D6FA}_{j}}=-\frac{1}{k_{\Vert }}\frac{\unicode[STIX]{x1D6E4}m_{j}}{\displaystyle \left(p_{\Vert }-\frac{\unicode[STIX]{x1D714}}{k_{\Vert }}\unicode[STIX]{x1D6E4}m_{j}+n\frac{\unicode[STIX]{x1D6FA}_{0j}}{k_{\Vert }}m_{j}\right)}, & & \displaystyle\end{eqnarray}$$
where
is the Lorentz factor. We define the dimensionless parallel momentum
![]() $\bar{p}_{\Vert }\equiv p_{\Vert }/m_{j}c$
. The dimensionless parallel momentum associated with the relativistic pole is given by
$\bar{p}_{\Vert }\equiv p_{\Vert }/m_{j}c$
. The dimensionless parallel momentum associated with the relativistic pole is given by
We apply the technique proposed by Lerche (Reference Lerche1967) to transform (2.9) from the
![]() $(p_{\bot },p_{\Vert })$
coordinate system to the
$(p_{\bot },p_{\Vert })$
coordinate system to the
![]() $(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
coordinate system (see also Swanson Reference Swanson2002; Lazar & Schlickeiser Reference Lazar and Schlickeiser2006; López et al.
Reference López, Moya, Muñoz, Viñas and Valdivia2014, Reference López, Moya, Navarro, Araneda, Muñoz, Viñas and Valdivia2016). This transformation yields
$(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
coordinate system (see also Swanson Reference Swanson2002; Lazar & Schlickeiser Reference Lazar and Schlickeiser2006; López et al.
Reference López, Moya, Muñoz, Viñas and Valdivia2014, Reference López, Moya, Navarro, Araneda, Muñoz, Viñas and Valdivia2016). This transformation yields
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D74C}_{j} & = & \displaystyle 2\unicode[STIX]{x03C0}m_{j}^{3}c^{3}\frac{\unicode[STIX]{x1D714}_{\text{p}j}^{2}}{\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}_{0j}}\int _{1}^{\infty }\text{d}\unicode[STIX]{x1D6E4}\int _{-\sqrt{\unicode[STIX]{x1D6E4}^{2}-1}}^{+\sqrt{\unicode[STIX]{x1D6E4}^{2}-1}}\text{d}\bar{p}_{\Vert }\left[\hat{\boldsymbol{e}}_{\Vert }\hat{\boldsymbol{e}}_{\Vert }\frac{\unicode[STIX]{x1D6FA}_{0j}}{\unicode[STIX]{x1D714}}\bar{p}_{\Vert }\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}\bar{p}_{\Vert }}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{n=-\infty }^{+\infty }\frac{\unicode[STIX]{x1D6FA}_{0j}}{k_{\Vert }c}\left(\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}}+\frac{k_{\Vert }c}{\unicode[STIX]{x1D714}}\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}\bar{p}_{\Vert }}\right)\frac{1}{\displaystyle \bar{p}_{\Vert }-\unicode[STIX]{x1D6E4}\frac{\unicode[STIX]{x1D714}}{k_{\Vert }c}+\frac{n\unicode[STIX]{x1D6FA}_{0j}}{k_{\Vert }c}}\bar{\unicode[STIX]{x1D64F}}_{n}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D74C}_{j} & = & \displaystyle 2\unicode[STIX]{x03C0}m_{j}^{3}c^{3}\frac{\unicode[STIX]{x1D714}_{\text{p}j}^{2}}{\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}_{0j}}\int _{1}^{\infty }\text{d}\unicode[STIX]{x1D6E4}\int _{-\sqrt{\unicode[STIX]{x1D6E4}^{2}-1}}^{+\sqrt{\unicode[STIX]{x1D6E4}^{2}-1}}\text{d}\bar{p}_{\Vert }\left[\hat{\boldsymbol{e}}_{\Vert }\hat{\boldsymbol{e}}_{\Vert }\frac{\unicode[STIX]{x1D6FA}_{0j}}{\unicode[STIX]{x1D714}}\bar{p}_{\Vert }\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}\bar{p}_{\Vert }}\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\mathop{\sum }_{n=-\infty }^{+\infty }\frac{\unicode[STIX]{x1D6FA}_{0j}}{k_{\Vert }c}\left(\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}}+\frac{k_{\Vert }c}{\unicode[STIX]{x1D714}}\frac{\unicode[STIX]{x2202}f_{0j}}{\unicode[STIX]{x2202}\bar{p}_{\Vert }}\right)\frac{1}{\displaystyle \bar{p}_{\Vert }-\unicode[STIX]{x1D6E4}\frac{\unicode[STIX]{x1D714}}{k_{\Vert }c}+\frac{n\unicode[STIX]{x1D6FA}_{0j}}{k_{\Vert }c}}\bar{\unicode[STIX]{x1D64F}}_{n}\right],\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle \bar{\unicode[STIX]{x1D64F}_{n}}\equiv \left(\begin{array}{@{}ccc@{}}\displaystyle \frac{n^{2}\text{J}_{n}^{2}}{\bar{z}^{2}} & \displaystyle \frac{\text{i}n\text{J}_{n}\text{J}_{n}^{\prime }}{\bar{z}}\bar{p}_{\bot } & \displaystyle \frac{n\text{J}_{n}^{2}\bar{p}_{\Vert }}{\bar{z}}\\ \displaystyle -\frac{\text{i}n\text{J}_{n}\text{J}_{n}^{\prime }}{\bar{z}}\bar{p}_{\bot } & \displaystyle (\text{J}_{n}^{\prime })^{2}\bar{p}_{\bot }^{2} & \displaystyle -\text{i}\text{J}_{n}\text{J}_{n}^{\prime }\bar{p}_{\Vert }\bar{p}_{\bot }\\ \displaystyle \frac{n\text{J}_{n}^{2}\bar{p}_{\Vert }}{\bar{z}} & \displaystyle \text{i}\text{J}_{n}\text{J}_{n}^{\prime }\bar{p}_{\Vert }\bar{p}_{\bot } & \displaystyle \text{J}_{n}^{2}\bar{p}_{\Vert }^{2}\end{array}\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bar{\unicode[STIX]{x1D64F}_{n}}\equiv \left(\begin{array}{@{}ccc@{}}\displaystyle \frac{n^{2}\text{J}_{n}^{2}}{\bar{z}^{2}} & \displaystyle \frac{\text{i}n\text{J}_{n}\text{J}_{n}^{\prime }}{\bar{z}}\bar{p}_{\bot } & \displaystyle \frac{n\text{J}_{n}^{2}\bar{p}_{\Vert }}{\bar{z}}\\ \displaystyle -\frac{\text{i}n\text{J}_{n}\text{J}_{n}^{\prime }}{\bar{z}}\bar{p}_{\bot } & \displaystyle (\text{J}_{n}^{\prime })^{2}\bar{p}_{\bot }^{2} & \displaystyle -\text{i}\text{J}_{n}\text{J}_{n}^{\prime }\bar{p}_{\Vert }\bar{p}_{\bot }\\ \displaystyle \frac{n\text{J}_{n}^{2}\bar{p}_{\Vert }}{\bar{z}} & \displaystyle \text{i}\text{J}_{n}\text{J}_{n}^{\prime }\bar{p}_{\Vert }\bar{p}_{\bot } & \displaystyle \text{J}_{n}^{2}\bar{p}_{\Vert }^{2}\end{array}\right), & & \displaystyle\end{eqnarray}$$
![]() $\bar{p}_{\bot }\equiv \sqrt{\unicode[STIX]{x1D6E4}^{2}-1-\bar{p}_{\Vert }^{2}}$
,
$\bar{p}_{\bot }\equiv \sqrt{\unicode[STIX]{x1D6E4}^{2}-1-\bar{p}_{\Vert }^{2}}$
,
![]() $\bar{z}\equiv k_{\bot }c/\unicode[STIX]{x1D6FA}_{0j}$
and the Bessel functions are evaluated as
$\bar{z}\equiv k_{\bot }c/\unicode[STIX]{x1D6FA}_{0j}$
and the Bessel functions are evaluated as
![]() $\text{J}_{n}\equiv \text{J}_{n}(\bar{z}\bar{p}_{\bot })$
. Whenever ALPS performs a relativistic calculation and
$\text{J}_{n}\equiv \text{J}_{n}(\bar{z}\bar{p}_{\bot })$
. Whenever ALPS performs a relativistic calculation and
the code automatically transforms from
![]() $(p_{\bot },p_{\Vert })$
to
$(p_{\bot },p_{\Vert })$
to
![]() $(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
coordinates and applies the polyharmonic-spline algorithm described in appendix C to create an equally spaced and homogeneous grid in
$(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
coordinates and applies the polyharmonic-spline algorithm described in appendix C to create an equally spaced and homogeneous grid in
![]() $(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
coordinates. In this coordinate system, we perform the integration near poles and the analytic continuation in the same way as described in §§ 3.1 and 3.2, but using the relativistic parallel momentum associated with the pole from (3.15). For reasons of numerical performance, we use the integration based on (3.16) only if there is a pole within the integration domain. Otherwise, we employ the faster integration method based on (2.9) even in the relativistic case.
$(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
coordinates. In this coordinate system, we perform the integration near poles and the analytic continuation in the same way as described in §§ 3.1 and 3.2, but using the relativistic parallel momentum associated with the pole from (3.15). For reasons of numerical performance, we use the integration based on (3.16) only if there is a pole within the integration domain. Otherwise, we employ the faster integration method based on (2.9) even in the relativistic case.
4 Test cases and results
In this section, we compare ALPS with known reference cases based on either our own or previously published results.
4.1 Maxwellian distributions
There are numerous codes for the hot-plasma dispersion relation in a plasma with Maxwellian or bi-Maxwellian background distributions. We use our code PLUME (Klein & Howes Reference Klein and Howes2015) for an electron–proton plasma and calculate the dispersion relations of Alfvén/ion-cyclotron (A/IC) and fast-magnetosonic/whistler (FM/W) waves. We then set up Maxwellian
![]() $f_{0}$
tables with the same parameters as those used with PLUME and calculate the dispersion relations based on these
$f_{0}$
tables with the same parameters as those used with PLUME and calculate the dispersion relations based on these
![]() $f_{0}$
tables with ALPS. We compare the PLUME and ALPS results for quasi-parallel and quasi-perpendicular propagation in figure 1. The panels show both the real part of the frequency
$f_{0}$
tables with ALPS. We compare the PLUME and ALPS results for quasi-parallel and quasi-perpendicular propagation in figure 1. The panels show both the real part of the frequency
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
and its imaginary part
$\unicode[STIX]{x1D714}_{\text{r}}$
and its imaginary part
![]() $\unicode[STIX]{x1D6FE}$
as functions of the parallel and perpendicular wavenumbers, respectively. We use
$\unicode[STIX]{x1D6FE}$
as functions of the parallel and perpendicular wavenumbers, respectively. We use
![]() $\unicode[STIX]{x1D6FD}_{\bot j}=\unicode[STIX]{x1D6FD}_{\Vert j}=1$
for both protons and electrons, and
$\unicode[STIX]{x1D6FD}_{\bot j}=\unicode[STIX]{x1D6FD}_{\Vert j}=1$
for both protons and electrons, and
![]() $v_{\text{A}}/c=10^{-4}$
, where
$v_{\text{A}}/c=10^{-4}$
, where
![]() $\unicode[STIX]{x1D6FD}_{\bot j}\equiv 8\unicode[STIX]{x03C0}n_{0j}k_{\text{B}}T_{\bot j}/B_{0}^{2}$
and
$\unicode[STIX]{x1D6FD}_{\bot j}\equiv 8\unicode[STIX]{x03C0}n_{0j}k_{\text{B}}T_{\bot j}/B_{0}^{2}$
and
![]() $\unicode[STIX]{x1D6FD}_{\Vert j}\equiv 8\unicode[STIX]{x03C0}n_{0j}k_{\text{B}}T_{\Vert j}/B_{0}^{2}$
. We normalise all frequencies in units of the proton-cyclotron frequency
$\unicode[STIX]{x1D6FD}_{\Vert j}\equiv 8\unicode[STIX]{x03C0}n_{0j}k_{\text{B}}T_{\Vert j}/B_{0}^{2}$
. We normalise all frequencies in units of the proton-cyclotron frequency
![]() $\unicode[STIX]{x1D6FA}_{0\text{p}}$
and all length scales in units of the proton skin depth
$\unicode[STIX]{x1D6FA}_{0\text{p}}$
and all length scales in units of the proton skin depth
![]() $d_{\text{p}}\equiv v_{\text{A}}/\unicode[STIX]{x1D6FA}_{0\text{p}}$
. The momentum-space resolution for the ALPS calculation in the quasi-parallel limit is
$d_{\text{p}}\equiv v_{\text{A}}/\unicode[STIX]{x1D6FA}_{0\text{p}}$
. The momentum-space resolution for the ALPS calculation in the quasi-parallel limit is
![]() $N_{\bot }=320$
,
$N_{\bot }=320$
,
![]() $N_{\Vert }=640$
,
$N_{\Vert }=640$
,
![]() $P_{\max ,\Vert \text{p}}=8m_{\text{p}}v_{\text{A}}$
and
$P_{\max ,\Vert \text{p}}=8m_{\text{p}}v_{\text{A}}$
and
![]() $P_{\max ,\Vert \text{e}}=0.19m_{\text{p}}v_{\text{A}}$
. In the quasi-perpendicular limit, we use
$P_{\max ,\Vert \text{e}}=0.19m_{\text{p}}v_{\text{A}}$
. In the quasi-perpendicular limit, we use
![]() $N_{\bot }=240$
,
$N_{\bot }=240$
,
![]() $N_{\Vert }=480$
,
$N_{\Vert }=480$
,
![]() $P_{\max ,\Vert \text{p}}=6m_{\text{p}}v_{\text{A}}$
and
$P_{\max ,\Vert \text{p}}=6m_{\text{p}}v_{\text{A}}$
and
![]() $P_{\max ,\Vert \text{e}}=0.14m_{\text{p}}v_{\text{A}}$
. In both cases, we set
$P_{\max ,\Vert \text{e}}=0.14m_{\text{p}}v_{\text{A}}$
. In both cases, we set
![]() $P_{\max ,\bot j}=P_{\max ,\Vert j}$
,
$P_{\max ,\bot j}=P_{\max ,\Vert j}$
,
![]() $J_{\max }=10^{-45}$
,
$J_{\max }=10^{-45}$
,
![]() $M_{\text{I}}=5$
,
$M_{\text{I}}=5$
,
![]() $M_{\text{P}}=100$
,
$M_{\text{P}}=100$
,
![]() $t_{\text{lim}}=0.01$
and scan through
$t_{\text{lim}}=0.01$
and scan through
![]() $\boldsymbol{k}$
-space in 256 logarithmically spaced steps from
$\boldsymbol{k}$
-space in 256 logarithmically spaced steps from
![]() $k_{\Vert }d_{\text{p}}=10^{-2}$
to
$k_{\Vert }d_{\text{p}}=10^{-2}$
to
![]() $k_{\Vert }d_{\text{p}}=10$
and
$k_{\Vert }d_{\text{p}}=10$
and
![]() $k_{\bot }d_{\text{p}}=10^{-2}$
to
$k_{\bot }d_{\text{p}}=10^{-2}$
to
![]() $k_{\bot }d_{\text{p}}=10$
, respectively. We study the accuracy of the results depending on the resolution in § A.1. Figure 1 shows that ALPS reproduces these Maxwellian examples very well. We note that these plasma parameters represent typical solar-wind conditions at 1 au.
$k_{\bot }d_{\text{p}}=10$
, respectively. We study the accuracy of the results depending on the resolution in § A.1. Figure 1 shows that ALPS reproduces these Maxwellian examples very well. We note that these plasma parameters represent typical solar-wind conditions at 1 au.

Figure 1. Dispersion relations for the A/IC wave and the FM/W wave in a Maxwellian plasma in quasi-parallel (a) and quasi-perpendicular (b) propagation. For the calculations shown on (a), we keep
![]() $k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\Vert }$
. For the calculations shown on (b), we keep
$k_{\Vert }$
. For the calculations shown on (b), we keep
![]() $k_{\Vert }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\Vert }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\bot }$
. The A/IC mode in quasi-perpendicular propagation corresponds to the kinetic Alfvén wave (KAW) at
$k_{\bot }$
. The A/IC mode in quasi-perpendicular propagation corresponds to the kinetic Alfvén wave (KAW) at
![]() $k_{\bot }d_{\text{p}}\gtrsim 1/\sqrt{\unicode[STIX]{x1D6FD}_{\Vert \text{p}}}$
. We compare ALPS with the standard Maxwellian solutions from PLUME for an electron–proton plasma with the same plasma parameters. Both numerical models agree well in both the real part
$k_{\bot }d_{\text{p}}\gtrsim 1/\sqrt{\unicode[STIX]{x1D6FD}_{\Vert \text{p}}}$
. We compare ALPS with the standard Maxwellian solutions from PLUME for an electron–proton plasma with the same plasma parameters. Both numerical models agree well in both the real part
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
of the frequency and its imaginary part
$\unicode[STIX]{x1D714}_{\text{r}}$
of the frequency and its imaginary part
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.

Figure 2. Comparison of dispersion maps from PLUME (a) and ALPS (b) for
![]() $k_{\bot }d_{\text{p}}=k_{\Vert }d_{\text{p}}=10^{-3}$
. The lines show isocontours of constant
$k_{\bot }d_{\text{p}}=k_{\Vert }d_{\text{p}}=10^{-3}$
. The lines show isocontours of constant
![]() $\lg |\text{det}\,{\mathcal{D}}|$
. The colour scheme varies from small
$\lg |\text{det}\,{\mathcal{D}}|$
. The colour scheme varies from small
![]() $\lg |\text{det}\,{\mathcal{D}}|$
in blue to large
$\lg |\text{det}\,{\mathcal{D}}|$
in blue to large
![]() $\lg |\text{det}\,{\mathcal{D}}|$
in red. Minima in this map correspond to solutions to the hot-plasma dispersion relation.
$\lg |\text{det}\,{\mathcal{D}}|$
in red. Minima in this map correspond to solutions to the hot-plasma dispersion relation.
In order to illustrate another representation of the plasma dispersion relation, we show a comparison of dispersion maps from PLUME and ALPS in figure 2. Dispersion maps are diagrams of isocontours of constant
![]() $\lg |\text{det}\,{\mathcal{D}}|$
, where
$\lg |\text{det}\,{\mathcal{D}}|$
, where
![]() ${\mathcal{D}}$
is the tensor from (2.12), in the
${\mathcal{D}}$
is the tensor from (2.12), in the
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
–
$\unicode[STIX]{x1D714}_{\text{r}}$
–
![]() $\unicode[STIX]{x1D6FE}$
plane. Solutions to the hot-plasma dispersion relation appear as local minima in these diagrams. After calculating a dispersion map for a given
$\unicode[STIX]{x1D6FE}$
plane. Solutions to the hot-plasma dispersion relation appear as local minima in these diagrams. After calculating a dispersion map for a given
![]() $\boldsymbol{k}$
, ALPS automatically determines the locations of its local minima in terms of
$\boldsymbol{k}$
, ALPS automatically determines the locations of its local minima in terms of
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}$
and
![]() $\unicode[STIX]{x1D6FE}$
. These minima represent ideal initial guesses for the Newton-secant root-finding search when scanning through
$\unicode[STIX]{x1D6FE}$
. These minima represent ideal initial guesses for the Newton-secant root-finding search when scanning through
![]() $\boldsymbol{k}$
. Although the calculation of a dispersion map still requires the calculation of all
$\boldsymbol{k}$
. Although the calculation of a dispersion map still requires the calculation of all
![]() $\unicode[STIX]{x1D74C}_{j}$
, it does not entail the application of the Newton-secant root-finding algorithm itself. We use a Maxwellian plasma model with
$\unicode[STIX]{x1D74C}_{j}$
, it does not entail the application of the Newton-secant root-finding algorithm itself. We use a Maxwellian plasma model with
![]() $\unicode[STIX]{x1D6FD}_{\bot j}=\unicode[STIX]{x1D6FD}_{\Vert j}=1$
for both protons and electrons,
$\unicode[STIX]{x1D6FD}_{\bot j}=\unicode[STIX]{x1D6FD}_{\Vert j}=1$
for both protons and electrons,
![]() $k_{\bot }d_{\text{p}}=k_{\Vert }d_{\text{p}}=10^{-3}$
and
$k_{\bot }d_{\text{p}}=k_{\Vert }d_{\text{p}}=10^{-3}$
and
![]() $v_{\text{A}}/c=10^{-4}$
. For the ALPS calculation, we use
$v_{\text{A}}/c=10^{-4}$
. For the ALPS calculation, we use
![]() $N_{\bot }=240$
,
$N_{\bot }=240$
,
![]() $N_{\Vert }=480$
,
$N_{\Vert }=480$
,
![]() $P_{\max ,\Vert \text{p}}=P_{\max ,\bot \text{p}}=6m_{\text{p}}v_{\text{A}}$
,
$P_{\max ,\Vert \text{p}}=P_{\max ,\bot \text{p}}=6m_{\text{p}}v_{\text{A}}$
,
![]() $P_{\max ,\Vert \text{e}}=P_{\max ,\bot \text{e}}=0.14m_{\text{p}}v_{\text{A}}$
,
$P_{\max ,\Vert \text{e}}=P_{\max ,\bot \text{e}}=0.14m_{\text{p}}v_{\text{A}}$
,
![]() $J_{\max }=10^{-45}$
,
$J_{\max }=10^{-45}$
,
![]() $M_{\text{I}}=5$
,
$M_{\text{I}}=5$
,
![]() $M_{\text{P}}=100$
and
$M_{\text{P}}=100$
and
![]() $t_{\text{lim}}=0.01$
. Both the PLUME and the ALPS calculations reveal seven solutions to the dispersion relation. We note that the point
$t_{\text{lim}}=0.01$
. Both the PLUME and the ALPS calculations reveal seven solutions to the dispersion relation. We note that the point
![]() $\unicode[STIX]{x1D714}_{\text{r}}=\unicode[STIX]{x1D6FE}=0$
is a maximum and does not represent a solution to the dispersion relation. The solutions at
$\unicode[STIX]{x1D714}_{\text{r}}=\unicode[STIX]{x1D6FE}=0$
is a maximum and does not represent a solution to the dispersion relation. The solutions at
![]() $\unicode[STIX]{x1D714}_{\text{r}}=\pm 10^{-3}\unicode[STIX]{x1D6FA}_{0\text{p}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}=\pm 10^{-3}\unicode[STIX]{x1D6FA}_{0\text{p}}$
and
![]() $\unicode[STIX]{x1D6FE}=-2.3\times 10^{-10}\unicode[STIX]{x1D6FA}_{0\text{p}}$
are the forward and backward propagating A/IC waves. The solutions at
$\unicode[STIX]{x1D6FE}=-2.3\times 10^{-10}\unicode[STIX]{x1D6FA}_{0\text{p}}$
are the forward and backward propagating A/IC waves. The solutions at
![]() $\unicode[STIX]{x1D714}_{\text{r}}=\pm 2\times 10^{-3}\unicode[STIX]{x1D6FA}_{0\text{p}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}=\pm 2\times 10^{-3}\unicode[STIX]{x1D6FA}_{0\text{p}}$
and
![]() $\unicode[STIX]{x1D6FE}=-5.4\times 10^{-5}\unicode[STIX]{x1D6FA}_{0\text{p}}$
are the forward and backward propagating FM/W waves. The solutions at
$\unicode[STIX]{x1D6FE}=-5.4\times 10^{-5}\unicode[STIX]{x1D6FA}_{0\text{p}}$
are the forward and backward propagating FM/W waves. The solutions at
![]() $\unicode[STIX]{x1D714}_{\text{r}}=\pm 1.2\times 10^{-3}\unicode[STIX]{x1D6FA}_{0\text{p}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}=\pm 1.2\times 10^{-3}\unicode[STIX]{x1D6FA}_{0\text{p}}$
and
![]() $\unicode[STIX]{x1D6FE}=-7.3\times 10^{-4}\unicode[STIX]{x1D6FA}_{0\text{p}}$
are the forward and backward propagating slow waves (ion-acoustic waves). Lastly, the solution at
$\unicode[STIX]{x1D6FE}=-7.3\times 10^{-4}\unicode[STIX]{x1D6FA}_{0\text{p}}$
are the forward and backward propagating slow waves (ion-acoustic waves). Lastly, the solution at
![]() $\unicode[STIX]{x1D714}_{\text{r}}=0$
and
$\unicode[STIX]{x1D714}_{\text{r}}=0$
and
![]() $\unicode[STIX]{x1D6FE}=-7.2\times 10^{-4}\unicode[STIX]{x1D6FA}_{0\text{p}}$
is the non-propagating slow mode, which is sometimes denoted ‘entropy mode’, (Verscharen et al.
Reference Verscharen, Chandran, Klein and Quataert2016; Verscharen, Chen & Wicks Reference Verscharen, Chen and Wicks2017). The comparison of both panels in figure 2 shows that ALPS reproduces these seven plasma modes under typical solar-wind conditions in the Maxwellian limit.
$\unicode[STIX]{x1D6FE}=-7.2\times 10^{-4}\unicode[STIX]{x1D6FA}_{0\text{p}}$
is the non-propagating slow mode, which is sometimes denoted ‘entropy mode’, (Verscharen et al.
Reference Verscharen, Chandran, Klein and Quataert2016; Verscharen, Chen & Wicks Reference Verscharen, Chen and Wicks2017). The comparison of both panels in figure 2 shows that ALPS reproduces these seven plasma modes under typical solar-wind conditions in the Maxwellian limit.

Figure 3. Comparison of dispersion relations for the A/IC instability (a) and the mirror-mode instability (b) from PLUME and ALPS. We use
![]() $T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. For the calculation of the A/IC instability, we keep
$T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. For the calculation of the A/IC instability, we keep
![]() $k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\Vert }$
. For the calculation of the mirror-mode instability, we keep the angle
$k_{\Vert }$
. For the calculation of the mirror-mode instability, we keep the angle
![]() $\unicode[STIX]{x1D703}=75^{\circ }$
constant and scan through
$\unicode[STIX]{x1D703}=75^{\circ }$
constant and scan through
![]() $|\boldsymbol{k}|$
.
$|\boldsymbol{k}|$
.
4.2 Anisotropic bi-Maxwellian distributions
PLUME, like most other standard hot-plasma dispersion-relation solvers, allows us to use anisotropic bi-Maxwellian representations for the background distribution functions. Such a configuration can lead to instability if the temperature anisotropy exceeds the threshold for an anisotropy-driven plasma instability. As an example for a propagating instability, we calculate the dispersion relation for the parallel A/IC instability (Harris Reference Harris1961; Davidson & Ogden Reference Davidson and Ogden1975; Yoon et al.
Reference Yoon, Seough, Khim, Kim, Kwon, Park, Parkh and Park2010), and as an example for a non-propagating instability, we calculate the dispersion relation for the mirror-mode instability (Rudakov & Sagdeev Reference Rudakov and Sagdeev1961; Tajiri Reference Tajiri1967; Southwood & Kivelson Reference Southwood and Kivelson1993). The thresholds for both of these instabilities fulfil
![]() $T_{\bot \text{p}}>T_{\Vert \text{p}}$
. For this demonstration, we use PLUME to calculate
$T_{\bot \text{p}}>T_{\Vert \text{p}}$
. For this demonstration, we use PLUME to calculate
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}$
and
![]() $\unicode[STIX]{x1D6FE}$
as functions of the wavenumber in a plasma with bi-Maxwellian protons and Maxwellian electrons using
$\unicode[STIX]{x1D6FE}$
as functions of the wavenumber in a plasma with bi-Maxwellian protons and Maxwellian electrons using
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=\unicode[STIX]{x1D6FD}_{\bot \text{e}}=1$
,
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=\unicode[STIX]{x1D6FD}_{\bot \text{e}}=1$
,
![]() $T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
and
$T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
and
![]() $v_{\text{A}}/c=10^{-4}$
. We then set-up bi-Maxwellian
$v_{\text{A}}/c=10^{-4}$
. We then set-up bi-Maxwellian
![]() $f_{0}$
tables with the same parameters and calculate the dispersion relations for both instabilities with ALPS. We show the results in figure 3. For the ALPS calculation, we use
$f_{0}$
tables with the same parameters and calculate the dispersion relations for both instabilities with ALPS. We show the results in figure 3. For the ALPS calculation, we use
![]() $N_{\bot }=320$
,
$N_{\bot }=320$
,
![]() $N_{\Vert }=640$
,
$N_{\Vert }=640$
,
![]() $P_{\max ,\Vert \text{p}}=8m_{\text{p}}v_{\text{A}}$
,
$P_{\max ,\Vert \text{p}}=8m_{\text{p}}v_{\text{A}}$
,
![]() $P_{\max ,\bot \text{p}}=13.9m_{\text{p}}v_{\text{A}}$
,
$P_{\max ,\bot \text{p}}=13.9m_{\text{p}}v_{\text{A}}$
,
![]() $P_{\max ,\Vert \text{e}}=P_{\max ,\bot \text{e}}=0.19m_{\text{p}}v_{\text{A}}$
,
$P_{\max ,\Vert \text{e}}=P_{\max ,\bot \text{e}}=0.19m_{\text{p}}v_{\text{A}}$
,
![]() $J_{\max }=10^{-45}$
,
$J_{\max }=10^{-45}$
,
![]() $M_{\text{I}}=5$
,
$M_{\text{I}}=5$
,
![]() $M_{\text{P}}=100$
and
$M_{\text{P}}=100$
and
![]() $t_{\text{lim}}=0.01$
. For the A/IC instability, we scan through
$t_{\text{lim}}=0.01$
. For the A/IC instability, we scan through
![]() $k_{\Vert }$
from
$k_{\Vert }$
from
![]() $k_{\Vert }d_{\text{p}}=10^{-2}$
to
$k_{\Vert }d_{\text{p}}=10^{-2}$
to
![]() $k_{\Vert }d_{\text{p}}=10$
in 256 logarithmically spaced steps. For the mirror-mode instability, we scan through
$k_{\Vert }d_{\text{p}}=10$
in 256 logarithmically spaced steps. For the mirror-mode instability, we scan through
![]() $k$
from
$k$
from
![]() $kd_{\text{p}}=10^{-2}$
to
$kd_{\text{p}}=10^{-2}$
to
![]() $kd_{\text{p}}=5$
in 154 logarithmically spaced steps and keep the angle
$kd_{\text{p}}=5$
in 154 logarithmically spaced steps and keep the angle
![]() $\unicode[STIX]{x1D703}\equiv \text{arcsin}(k_{\bot }/k)=75^{\circ }$
constant. We study the accuracy of these results depending on the resolution in § A.2.
$\unicode[STIX]{x1D703}\equiv \text{arcsin}(k_{\bot }/k)=75^{\circ }$
constant. We study the accuracy of these results depending on the resolution in § A.2.
Both PLUME and ALPS show that the A/IC wave and the mirror mode are unstable in different wave-vector ranges for the given parameter set. The good agreement between the PLUME solutions and the ALPS solutions shows that ALPS successfully calculates the dispersion relations of both instabilities in a bi-Maxwellian plasma. Although the correct mirror mode exhibits
![]() $\unicode[STIX]{x1D714}_{\text{r}}=0$
, the ALPS solution shows a very small yet finite
$\unicode[STIX]{x1D714}_{\text{r}}=0$
, the ALPS solution shows a very small yet finite
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
. We discuss this error and its dependence on the velocity-space resolution in § A.2.
$\unicode[STIX]{x1D714}_{\text{r}}$
. We discuss this error and its dependence on the velocity-space resolution in § A.2.
4.3 Anisotropic
 $\unicode[STIX]{x1D705}$
-distributions
$\unicode[STIX]{x1D705}$
-distributions
Astfalk et al. (Reference Astfalk, Görler and Jenko2015) developed the code DSHARK to calculate dispersion relations in plasmas with bi-
![]() $\unicode[STIX]{x1D705}$
-distributions. As one example, these authors discuss the FM/W instability in an anisotropic electron–proton plasma with
$\unicode[STIX]{x1D705}$
-distributions. As one example, these authors discuss the FM/W instability in an anisotropic electron–proton plasma with
![]() $\unicode[STIX]{x1D705}_{\text{p}}=\unicode[STIX]{x1D705}_{\text{e}}=8$
,
$\unicode[STIX]{x1D705}_{\text{p}}=\unicode[STIX]{x1D705}_{\text{e}}=8$
,
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=2$
,
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=2$
,
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=4$
,
$\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=4$
,
![]() $T_{\bot \text{p}}/T_{\Vert \text{p}}=0.4$
and
$T_{\bot \text{p}}/T_{\Vert \text{p}}=0.4$
and
![]() $T_{\bot \text{e}}/T_{\Vert \text{e}}=0.5$
(see figure 1 from Astfalk et al.
Reference Astfalk, Görler and Jenko2015). The angle between
$T_{\bot \text{e}}/T_{\Vert \text{e}}=0.5$
(see figure 1 from Astfalk et al.
Reference Astfalk, Görler and Jenko2015). The angle between
![]() $\boldsymbol{k}$
and
$\boldsymbol{k}$
and
![]() $\boldsymbol{B}_{0}$
is constant for this calculation and set to
$\boldsymbol{B}_{0}$
is constant for this calculation and set to
![]() $\unicode[STIX]{x1D703}=0.001^{\circ }$
. We use DSHARK to reproduce this test case and set up
$\unicode[STIX]{x1D703}=0.001^{\circ }$
. We use DSHARK to reproduce this test case and set up
![]() $\unicode[STIX]{x1D705}$
-distributed
$\unicode[STIX]{x1D705}$
-distributed
![]() $f_{0}$
tables with the same parameters in order to compare the DSHARK results with ALPS. We show this comparison in figure 4. In ALPS, we use
$f_{0}$
tables with the same parameters in order to compare the DSHARK results with ALPS. We show this comparison in figure 4. In ALPS, we use
![]() $N_{\bot }=400$
,
$N_{\bot }=400$
,
![]() $N_{\Vert }=800$
,
$N_{\Vert }=800$
,
![]() $P_{\max ,\Vert \text{p}}=10m_{\text{p}}v_{\text{A}}$
,
$P_{\max ,\Vert \text{p}}=10m_{\text{p}}v_{\text{A}}$
,
![]() $P_{\max ,\bot \text{p}}=6.32m_{\text{p}}v_{\text{A}}$
,
$P_{\max ,\bot \text{p}}=6.32m_{\text{p}}v_{\text{A}}$
,
![]() $P_{\max ,\Vert \text{e}}=0.33m_{\text{p}}v_{\text{A}}$
,
$P_{\max ,\Vert \text{e}}=0.33m_{\text{p}}v_{\text{A}}$
,
![]() $P_{\max ,\bot \text{e}}=0.23m_{\text{p}}v_{\text{A}}$
,
$P_{\max ,\bot \text{e}}=0.23m_{\text{p}}v_{\text{A}}$
,
![]() $J_{\max }=10^{-45}$
,
$J_{\max }=10^{-45}$
,
![]() $M_{\text{I}}=5$
,
$M_{\text{I}}=5$
,
![]() $M_{\text{P}}=500$
,
$M_{\text{P}}=500$
,
![]() $t_{\text{lim}}=0.01$
and
$t_{\text{lim}}=0.01$
and
![]() $v_{\text{A}}/c=10^{-4}$
. We scan through
$v_{\text{A}}/c=10^{-4}$
. We scan through
![]() $k_{\Vert }$
from
$k_{\Vert }$
from
![]() $k_{\Vert }d_{p\text{}}=10^{-1}$
to
$k_{\Vert }d_{p\text{}}=10^{-1}$
to
![]() $k_{\Vert }d_{\text{p}}\approx 3.42$
, where
$k_{\Vert }d_{\text{p}}\approx 3.42$
, where
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
changes its sign after 87 logarithmically spaced steps.
$\unicode[STIX]{x1D714}_{\text{r}}$
changes its sign after 87 logarithmically spaced steps.

Figure 4. Comparison of dispersion relations of the FM/W instability in a
![]() $\unicode[STIX]{x1D705}$
-distributed plasma from DSHARK and ALPS. In both plasma models, we keep
$\unicode[STIX]{x1D705}$
-distributed plasma from DSHARK and ALPS. In both plasma models, we keep
![]() $\unicode[STIX]{x1D703}=0.001^{\circ }$
constant and scan through
$\unicode[STIX]{x1D703}=0.001^{\circ }$
constant and scan through
![]() $k_{\Vert }$
. (a) shows the real part of the wave frequency, and (b) shows its imaginary part.
$k_{\Vert }$
. (a) shows the real part of the wave frequency, and (b) shows its imaginary part.
ALPS reproduces the DSHARK results for the FM/W instability well. The results also agree with the previous work by Lazar et al. (Reference Lazar, Poedts and Schlickeiser2011).
4.4 Relativistic Jüttner distributions
As one example for a dispersion relation in a relativistic plasma, we reproduce the results by López et al. (Reference López, Moya, Muñoz, Viñas and Valdivia2014) for an electron–positron pair plasma with a Jüttner distribution using
![]() $v_{\text{A}}/c=1$
,
$v_{\text{A}}/c=1$
,
![]() $m_{\text{p}}=m_{\text{e}}$
,
$m_{\text{p}}=m_{\text{e}}$
,
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=(0.2,0.4,1.0)$
and
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=(0.2,0.4,1.0)$
and
![]() $T_{\bot j}=T_{\Vert j}$
for both positrons and electrons. We set up a Jüttner-distributed
$T_{\bot j}=T_{\Vert j}$
for both positrons and electrons. We set up a Jüttner-distributed
![]() $f_{0}$
table with the same parameters and calculate the dispersion relations of the A/IC wave and the Ordinary wave (O-mode) in the plasma, keeping the perpendicular wavenumber constant at
$f_{0}$
table with the same parameters and calculate the dispersion relations of the A/IC wave and the Ordinary wave (O-mode) in the plasma, keeping the perpendicular wavenumber constant at
![]() $k_{\bot }d_{\text{p}}=10^{-3}$
. We use
$k_{\bot }d_{\text{p}}=10^{-3}$
. We use
![]() $N_{\bot }=30$
,
$N_{\bot }=30$
,
![]() $N_{\Vert }=60$
,
$N_{\Vert }=60$
,
![]() $P_{\max }=5m_{\text{p}}v_{\text{A}}$
,
$P_{\max }=5m_{\text{p}}v_{\text{A}}$
,
![]() $J_{\max }=10^{-45}$
,
$J_{\max }=10^{-45}$
,
![]() $M_{\text{I}}=5$
,
$M_{\text{I}}=5$
,
![]() $M_{\text{P}}=300$
and
$M_{\text{P}}=300$
and
![]() $t_{\text{lim}}=0.01$
. Our interpolation method transforms the
$t_{\text{lim}}=0.01$
. Our interpolation method transforms the
![]() $(p_{\bot },p_{\Vert })$
grid to the
$(p_{\bot },p_{\Vert })$
grid to the
![]() $(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
grid with
$(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
grid with
![]() $N_{\unicode[STIX]{x1D6E4}}=500$
and
$N_{\unicode[STIX]{x1D6E4}}=500$
and
![]() $N_{\bar{p}_{\Vert }}=500$
steps in
$N_{\bar{p}_{\Vert }}=500$
steps in
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\bar{p}_{\Vert }$
, respectively. We scan through
$\bar{p}_{\Vert }$
, respectively. We scan through
![]() $k_{\Vert }$
from
$k_{\Vert }$
from
![]() $k_{\Vert }d_{\text{p}}=10^{-1}$
to
$k_{\Vert }d_{\text{p}}=10^{-1}$
to
![]() $k_{\Vert }d_{\text{p}}=10$
in 128 logarithmically spaced steps. We show the results in figure 5. López et al. (Reference López, Moya, Muñoz, Viñas and Valdivia2014) show their results for these parameters in their figure 1. Our comparison with the ALPS dispersion relation in figure 5 shows a good agreement and confirms our relativistic model. The deviation between the results from López et al. (Reference López, Moya, Muñoz, Viñas and Valdivia2014) and ALPS is only visible in the real part of the frequency at the large-
$k_{\Vert }d_{\text{p}}=10$
in 128 logarithmically spaced steps. We show the results in figure 5. López et al. (Reference López, Moya, Muñoz, Viñas and Valdivia2014) show their results for these parameters in their figure 1. Our comparison with the ALPS dispersion relation in figure 5 shows a good agreement and confirms our relativistic model. The deviation between the results from López et al. (Reference López, Moya, Muñoz, Viñas and Valdivia2014) and ALPS is only visible in the real part of the frequency at the large-
![]() $k_{\Vert }$
/low-
$k_{\Vert }$
/low-
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
end of the A/IC branches.
$\unicode[STIX]{x1D714}_{\text{r}}$
end of the A/IC branches.

Figure 5. Dispersion relations of the quasi-parallel A/IC wave (solutions at low
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
) and the ordinary wave (solutions at high
$\unicode[STIX]{x1D714}_{\text{r}}$
) and the ordinary wave (solutions at high
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
) in a relativistic electron–positron pair plasma with Jüttner distributions. We keep
$\unicode[STIX]{x1D714}_{\text{r}}$
) in a relativistic electron–positron pair plasma with Jüttner distributions. We keep
![]() $k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\Vert }$
. (a) shows the real part of the frequency, and (b) shows the imaginary part of the frequency. The lines show ALPS solutions, and the crosses show the results from figure 1 of López et al. (Reference López, Moya, Muñoz, Viñas and Valdivia2014). The three colours correspond to
$k_{\Vert }$
. (a) shows the real part of the frequency, and (b) shows the imaginary part of the frequency. The lines show ALPS solutions, and the crosses show the results from figure 1 of López et al. (Reference López, Moya, Muñoz, Viñas and Valdivia2014). The three colours correspond to
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=0.2$
(red),
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=0.2$
(red),
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=0.4$
(green) and
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=0.4$
(green) and
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=1.0$
(blue) in both panels and for both modes.
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=1.0$
(blue) in both panels and for both modes.
5 Discussion and conclusions
ALPS solves the relativistic and non-relativistic hot-plasma dispersion relations in a plasma with arbitrary background distribution functions. We have benchmarked ALPS against existing codes by comparing dispersion relations for waves and instabilities in Maxwellian, bi-Maxwellian,
![]() $\unicode[STIX]{x1D705}$
-distributed and relativistic Jüttner-distributed plasmas. In all cases, we find that ALPS agrees well with existing codes. This finding encourages us to apply ALPS to yet unexplored plasma environments in future work. We note that we have only tested ALPS in the regime
$\unicode[STIX]{x1D705}$
-distributed and relativistic Jüttner-distributed plasmas. In all cases, we find that ALPS agrees well with existing codes. This finding encourages us to apply ALPS to yet unexplored plasma environments in future work. We note that we have only tested ALPS in the regime
![]() $k\unicode[STIX]{x1D70C}_{\text{e}}\ll 1$
and
$k\unicode[STIX]{x1D70C}_{\text{e}}\ll 1$
and
![]() $kd_{\text{e}}\ll 1$
thus far, where
$kd_{\text{e}}\ll 1$
thus far, where
![]() $\unicode[STIX]{x1D70C}_{\text{e}}\equiv w_{\bot \text{e}}/|\unicode[STIX]{x1D6FA}_{0\text{e}}|$
. There is no numerical limitation, however, that prevents us from applying the code to larger wavenumbers at or beyond electron scales.
$\unicode[STIX]{x1D70C}_{\text{e}}\equiv w_{\bot \text{e}}/|\unicode[STIX]{x1D6FA}_{0\text{e}}|$
. There is no numerical limitation, however, that prevents us from applying the code to larger wavenumbers at or beyond electron scales.
An important application of ALPS will be the analysis of distribution functions measured by spacecraft in the solar wind. ALPS includes the necessary numerical framework to preprocess and format the spacecraft data so that they can serve as
![]() $f_{0}$
tables for direct input (see appendix C). Especially, the upcoming missions Solar Orbiter and Parker Solar Probe will deliver plasma measurements with unprecedented energy and time resolution in the solar wind that will serve as the ideal input for ALPS. The vast majority of previous kinetic studies of waves and instabilities relied on bi-Maxwellian fits to the observed distribution functions and the use of a standard bi-Maxwellian code to solve the hot-plasma dispersion relation such as WHAMP, PLUME or NHDS. Our approach allows us, however, to relax the bi-Maxwellian assumption and to analyse the plasma behaviour more realistically. A great advantage of standard bi-Maxwellian solvers is their very high speed when solving the dispersion relation. The plots of dispersion relations shown in this paper require an ALPS run time between about one and ten hours on 32 processor cores, while PLUME solves the same dispersion relation for a bi-Maxwellian plasma within a few seconds. Therefore, we recommend the use of standard bi-Maxwellian solvers or solvers for
$f_{0}$
tables for direct input (see appendix C). Especially, the upcoming missions Solar Orbiter and Parker Solar Probe will deliver plasma measurements with unprecedented energy and time resolution in the solar wind that will serve as the ideal input for ALPS. The vast majority of previous kinetic studies of waves and instabilities relied on bi-Maxwellian fits to the observed distribution functions and the use of a standard bi-Maxwellian code to solve the hot-plasma dispersion relation such as WHAMP, PLUME or NHDS. Our approach allows us, however, to relax the bi-Maxwellian assumption and to analyse the plasma behaviour more realistically. A great advantage of standard bi-Maxwellian solvers is their very high speed when solving the dispersion relation. The plots of dispersion relations shown in this paper require an ALPS run time between about one and ten hours on 32 processor cores, while PLUME solves the same dispersion relation for a bi-Maxwellian plasma within a few seconds. Therefore, we recommend the use of standard bi-Maxwellian solvers or solvers for
![]() $\unicode[STIX]{x1D705}$
-distributed plasmas to determine an adequate initial guess before using ALPS whenever the
$\unicode[STIX]{x1D705}$
-distributed plasmas to determine an adequate initial guess before using ALPS whenever the
![]() $f_{0}$
table is close to a bi-Maxwellian or
$f_{0}$
table is close to a bi-Maxwellian or
![]() $\unicode[STIX]{x1D705}$
-distribution, respectively. Future comparisons of the results from standard codes such as PLUME with the results from ALPS will help to evaluate the quality of the previous bi-Maxwellian approaches and to refine our understanding of the role of instabilities in collisionless plasmas based on the actual distribution functions. For instance, our knowledge of the realistic value of certain instability thresholds is still very limited. Some in situ observations of kinetic plasma features in the solar wind lie above the thresholds of kinetic instabilities when calculated based on bi-Maxwellian background distributions (see, for example, Isenberg Reference Isenberg2012). The general conjecture is, however, that the plasma is limited by the lowest instability threshold. A more realistic calculation based on the actual distribution functions may resolve this discrepancy. This concept applies, for example, to anisotropy-driven instabilities such as the A/IC instability (Hellinger et al.
Reference Hellinger, Trávníček, Kasper and Lazarus2006; Bale et al.
Reference Bale, Kasper, Howes, Quataert, Salem and Sundkvist2009; Maruca, Kasper & Gary Reference Maruca, Kasper and Gary2012) or beam-driven instabilities such as the FM/W instability (Reisenfeld et al.
Reference Reisenfeld, Gary, Gosling, Steinberg, McComas, Goldstein and Neugebauer2001; Verscharen, Bourouaine & Chandran Reference Verscharen, Bourouaine and Chandran2013; Verscharen & Chandran Reference Verscharen and Chandran2013). Also non-thermal electron configurations, which are known to carry a significant heat flux into the solar wind, require a non-bi-Maxwellian representation for the determination of the relevant instabilities that limit their heat flux (Feldman et al.
Reference Feldman, Asbridge, Bame, Montgomery and Gary1975; Pilipp et al.
Reference Pilipp, Muehlhaeuser, Miggenrieder, Montgomery and Rosenbauer1987a
; Pulupa et al.
Reference Pulupa, Salem, Horaites and Bale2011; Salem et al.
Reference Salem, Pulupa, Verscharen, Bale and Chandran2013). Another field of application of ALPS is the study of highly non-thermal plasma configurations related to reconnection events (Phan et al.
Reference Phan, Gosling, Davis, Skoug, Øieroset, Lin, Lepping, McComas, Smith and Reme2006; Gosling Reference Gosling2007; Gosling et al.
Reference Gosling, Eriksson, Phan, Larson, Skoug and McComas2007; Egedal, Daughton & Le Reference Egedal, Daughton and Le2012; Egedal, Le & Daughton Reference Egedal, Le and Daughton2013). We also emphasise the applicability of ALPS for the determination of dispersion relations using distributions from numerical plasma simulations. Particle-in-cell or Eulerian plasma codes generate data directly suitable as
$\unicode[STIX]{x1D705}$
-distribution, respectively. Future comparisons of the results from standard codes such as PLUME with the results from ALPS will help to evaluate the quality of the previous bi-Maxwellian approaches and to refine our understanding of the role of instabilities in collisionless plasmas based on the actual distribution functions. For instance, our knowledge of the realistic value of certain instability thresholds is still very limited. Some in situ observations of kinetic plasma features in the solar wind lie above the thresholds of kinetic instabilities when calculated based on bi-Maxwellian background distributions (see, for example, Isenberg Reference Isenberg2012). The general conjecture is, however, that the plasma is limited by the lowest instability threshold. A more realistic calculation based on the actual distribution functions may resolve this discrepancy. This concept applies, for example, to anisotropy-driven instabilities such as the A/IC instability (Hellinger et al.
Reference Hellinger, Trávníček, Kasper and Lazarus2006; Bale et al.
Reference Bale, Kasper, Howes, Quataert, Salem and Sundkvist2009; Maruca, Kasper & Gary Reference Maruca, Kasper and Gary2012) or beam-driven instabilities such as the FM/W instability (Reisenfeld et al.
Reference Reisenfeld, Gary, Gosling, Steinberg, McComas, Goldstein and Neugebauer2001; Verscharen, Bourouaine & Chandran Reference Verscharen, Bourouaine and Chandran2013; Verscharen & Chandran Reference Verscharen and Chandran2013). Also non-thermal electron configurations, which are known to carry a significant heat flux into the solar wind, require a non-bi-Maxwellian representation for the determination of the relevant instabilities that limit their heat flux (Feldman et al.
Reference Feldman, Asbridge, Bame, Montgomery and Gary1975; Pilipp et al.
Reference Pilipp, Muehlhaeuser, Miggenrieder, Montgomery and Rosenbauer1987a
; Pulupa et al.
Reference Pulupa, Salem, Horaites and Bale2011; Salem et al.
Reference Salem, Pulupa, Verscharen, Bale and Chandran2013). Another field of application of ALPS is the study of highly non-thermal plasma configurations related to reconnection events (Phan et al.
Reference Phan, Gosling, Davis, Skoug, Øieroset, Lin, Lepping, McComas, Smith and Reme2006; Gosling Reference Gosling2007; Gosling et al.
Reference Gosling, Eriksson, Phan, Larson, Skoug and McComas2007; Egedal, Daughton & Le Reference Egedal, Daughton and Le2012; Egedal, Le & Daughton Reference Egedal, Le and Daughton2013). We also emphasise the applicability of ALPS for the determination of dispersion relations using distributions from numerical plasma simulations. Particle-in-cell or Eulerian plasma codes generate data directly suitable as
![]() $f_{0}$
tables for ALPS. Some of these numerical simulations use (realistically or artificially) relativistic plasma conditions. Therefore, ALPS’s ability to include relativistic effects will be very useful for the study of the wave properties and the stability of simulated plasmas.
$f_{0}$
tables for ALPS. Some of these numerical simulations use (realistically or artificially) relativistic plasma conditions. Therefore, ALPS’s ability to include relativistic effects will be very useful for the study of the wave properties and the stability of simulated plasmas.
Our resolution studies in appendix A offer some insight into the necessary resolution of the
![]() $f_{0}$
tables for a reliable determination of the plasma dispersion relation. In the shown applications, a minimum resolution of about
$f_{0}$
tables for a reliable determination of the plasma dispersion relation. In the shown applications, a minimum resolution of about
![]() $N_{\bot }=40$
and
$N_{\bot }=40$
and
![]() $N_{\Vert }=80$
has proven to be necessary for a good agreement between ALPS and the test results for (bi-)Maxwellian distributions. In a future extension of ALPS, we will include Nyquist’s method to automatically determine the stability of directly observed distribution functions (Klein et al.
Reference Klein, Kasper, Korreck and Stevens2017, Reference Klein, Alterman, Stevens, Vech and Kasper2018). We also note that, in cases with
$N_{\Vert }=80$
has proven to be necessary for a good agreement between ALPS and the test results for (bi-)Maxwellian distributions. In a future extension of ALPS, we will include Nyquist’s method to automatically determine the stability of directly observed distribution functions (Klein et al.
Reference Klein, Kasper, Korreck and Stevens2017, Reference Klein, Alterman, Stevens, Vech and Kasper2018). We also note that, in cases with
![]() $k_{\Vert }\ll k_{\bot }$
and
$k_{\Vert }\ll k_{\bot }$
and
![]() $\unicode[STIX]{x1D714}_{\text{r}}\ll \unicode[STIX]{x1D6FA}_{\text{p}0}$
, the gyrokinetic limit is an appropriate simplification to the full hot-plasma dispersion relation (Catto Reference Catto1978; Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Kunz et al.
Reference Kunz, Schekochihin, Chen, Abel and Cowley2015; Camporeale & Burgess Reference Camporeale and Burgess2017). The gyrokinetic dispersion relation does not require the sum over all
$\unicode[STIX]{x1D714}_{\text{r}}\ll \unicode[STIX]{x1D6FA}_{\text{p}0}$
, the gyrokinetic limit is an appropriate simplification to the full hot-plasma dispersion relation (Catto Reference Catto1978; Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Kunz et al.
Reference Kunz, Schekochihin, Chen, Abel and Cowley2015; Camporeale & Burgess Reference Camporeale and Burgess2017). The gyrokinetic dispersion relation does not require the sum over all
![]() $n\neq 0$
as in (2.9). Considering these lower numerical demands, it would be worthwhile to develop a gyrokinetic version of ALPS in the future.
$n\neq 0$
as in (2.9). Considering these lower numerical demands, it would be worthwhile to develop a gyrokinetic version of ALPS in the future.
Acknowledgement
We appreciate helpful comments and contributions from S. Markovskii and T. Brackett. The ALPS collaboration appreciates support from NASA grant NNX16AG81G. We present more details about the numerics on the website http://www.alps.space. The ALPS source code will be made publicly available on this website after our initial science phase. Computations were performed on Trillian, a Cray XE6m-200 supercomputer at UNH supported by the NSF MRI programme under grant PHY-1229408. D.V. was supported by the STFC Ernest Rutherford Fellowship ST/P003826/1. B.D.G.C. was supported in part by NASA grants NNX15AI80G and NNX17AI18G and NSF grant PHY-1500041. Work at UC Berkeley was supported in part by NSF/SHINE grant AGS-1622498 and NASA grants NNX14AJ70G, NNX16AI59G and NNX16AP95G.
Appendix A. Resolution studies
In order to understand the required resolution of the
![]() $f_{0}$
tables for calculations with ALPS, we compare results from PLUME with results from ALPS for the same plasma parameters using different resolutions in this appendix. For all calculations, we use
$f_{0}$
tables for calculations with ALPS, we compare results from PLUME with results from ALPS for the same plasma parameters using different resolutions in this appendix. For all calculations, we use
![]() $\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=1$
,
$\unicode[STIX]{x1D6FD}_{\Vert \text{p}}=\unicode[STIX]{x1D6FD}_{\Vert \text{e}}=1$
,
![]() $T_{\bot \text{e}}/T_{\Vert \text{e}}=1$
,
$T_{\bot \text{e}}/T_{\Vert \text{e}}=1$
,
![]() $J_{\max }=10^{-45}$
,
$J_{\max }=10^{-45}$
,
![]() $M_{\text{I}}=5$
,
$M_{\text{I}}=5$
,
![]() $M_{\text{P}}=100$
and
$M_{\text{P}}=100$
and
![]() $t_{\text{lim}}=0.01$
. A careful re-analysis of the A/IC-wave solutions using variations in
$t_{\text{lim}}=0.01$
. A careful re-analysis of the A/IC-wave solutions using variations in
![]() $M_{\text{I}}$
and
$M_{\text{I}}$
and
![]() $M_{\text{P}}$
over one order of magnitude each (not shown) reveals that the accuracy of the solutions depends only moderately on the numerical values of these parameters. We use
$M_{\text{P}}$
over one order of magnitude each (not shown) reveals that the accuracy of the solutions depends only moderately on the numerical values of these parameters. We use
![]() $P_{\max ,\Vert \text{p}}$
as a free parameter and set
$P_{\max ,\Vert \text{p}}$
as a free parameter and set
![]() $N_{\Vert }=2N_{\bot }$
,
$N_{\Vert }=2N_{\bot }$
,
![]() $P_{\max ,\Vert \text{e}}=P_{\max ,\bot \text{e}}=P_{\max ,\Vert \text{p}}\sqrt{m_{\text{e}}/m_{\text{p}}}$
and
$P_{\max ,\Vert \text{e}}=P_{\max ,\bot \text{e}}=P_{\max ,\Vert \text{p}}\sqrt{m_{\text{e}}/m_{\text{p}}}$
and
![]() $P_{\max ,\bot \text{p}}=P_{\max ,\Vert \text{p}}\sqrt{T_{\bot \text{p}}/T_{\Vert \text{p}}}$
. We apply the same resolutions for the scans in
$P_{\max ,\bot \text{p}}=P_{\max ,\Vert \text{p}}\sqrt{T_{\bot \text{p}}/T_{\Vert \text{p}}}$
. We apply the same resolutions for the scans in
![]() $\boldsymbol{k}$
-space as those used to derive the corresponding figures in § 4. We define the resolution in momentum as
$\boldsymbol{k}$
-space as those used to derive the corresponding figures in § 4. We define the resolution in momentum as
![]() $\unicode[STIX]{x0394}w_{j}\equiv P_{\max ,\Vert j}/(N_{\Vert }m_{j}w_{\Vert j})$
and the accuracy of the solution as
$\unicode[STIX]{x0394}w_{j}\equiv P_{\max ,\Vert j}/(N_{\Vert }m_{j}w_{\Vert j})$
and the accuracy of the solution as
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{\text{r}}/\unicode[STIX]{x1D714}_{\text{r}}\equiv |\unicode[STIX]{x1D714}_{\text{r},\text{ALPS}}-\unicode[STIX]{x1D714}_{\text{r},\text{PLUME}}|/\unicode[STIX]{x1D714}_{\text{r},\text{PLUME}}$
, where
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{\text{r}}/\unicode[STIX]{x1D714}_{\text{r}}\equiv |\unicode[STIX]{x1D714}_{\text{r},\text{ALPS}}-\unicode[STIX]{x1D714}_{\text{r},\text{PLUME}}|/\unicode[STIX]{x1D714}_{\text{r},\text{PLUME}}$
, where
![]() $\unicode[STIX]{x1D714}_{\text{r},\text{ALPS}}$
is the solution from ALPS and
$\unicode[STIX]{x1D714}_{\text{r},\text{ALPS}}$
is the solution from ALPS and
![]() $\unicode[STIX]{x1D714}_{\text{r},\text{PLUME}}$
is the solution from PLUME. For
$\unicode[STIX]{x1D714}_{\text{r},\text{PLUME}}$
is the solution from PLUME. For
![]() $\unicode[STIX]{x1D705}$
-distributions, the appropriate resolution depends on both
$\unicode[STIX]{x1D705}$
-distributions, the appropriate resolution depends on both
![]() $\unicode[STIX]{x1D6FD}_{\Vert j}$
and
$\unicode[STIX]{x1D6FD}_{\Vert j}$
and
![]() $\unicode[STIX]{x1D705}$
. Instead of giving general guidelines for the resolution, we, therefore, recommend case-by-case convergence studies when calculating dispersion relations in plasmas with
$\unicode[STIX]{x1D705}$
. Instead of giving general guidelines for the resolution, we, therefore, recommend case-by-case convergence studies when calculating dispersion relations in plasmas with
![]() $\unicode[STIX]{x1D705}$
-distributions.
$\unicode[STIX]{x1D705}$
-distributions.
A.1 Maxwellian distributions
In figure 6, we show a resolution study for the A/IC wave in quasi-parallel propagation in an isotropic Maxwellian plasma. This figure complements our solutions shown in figure 1. The four panels represent different values of
![]() $P_{\max ,\Vert j}$
. In each panel, the diagram at the top compares the real part of the frequency from five ALPS calculations with different
$P_{\max ,\Vert j}$
. In each panel, the diagram at the top compares the real part of the frequency from five ALPS calculations with different
![]() $\unicode[STIX]{x0394}w_{j}$
to the Maxwellian solutions from PLUME. The diagram at the bottom compares the ratio between
$\unicode[STIX]{x0394}w_{j}$
to the Maxwellian solutions from PLUME. The diagram at the bottom compares the ratio between
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
from the five ALPS calculations and
$\unicode[STIX]{x1D714}_{\text{r}}$
from the five ALPS calculations and
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
from PLUME. The line associated with a given parameter run ends whenever ALPS loses the solution as it scans through
$\unicode[STIX]{x1D714}_{\text{r}}$
from PLUME. The line associated with a given parameter run ends whenever ALPS loses the solution as it scans through
![]() $k_{\Vert }$
. For the parameters used in figure 6,
$k_{\Vert }$
. For the parameters used in figure 6,
![]() $P_{\max ,\Vert p}=8m_{\text{p}}w_{\text{p}}$
with a resolution finer than
$P_{\max ,\Vert p}=8m_{\text{p}}w_{\text{p}}$
with a resolution finer than
![]() $\unicode[STIX]{x0394}w_{j}=0.1$
leads to a very good agreement with the PLUME solutions for
$\unicode[STIX]{x0394}w_{j}=0.1$
leads to a very good agreement with the PLUME solutions for
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
. For wavenumbers below
$\unicode[STIX]{x1D714}_{\text{r}}$
. For wavenumbers below
![]() $1/d_{\text{p}}$
, a lower value of
$1/d_{\text{p}}$
, a lower value of
![]() $P_{\max ,\Vert \text{p}}$
is sufficient. Figure 7 shows the same as figure 6, but giving the imaginary part of the frequency instead of its real part. This figure confirms our finding regarding the optimal resolution.
$P_{\max ,\Vert \text{p}}$
is sufficient. Figure 7 shows the same as figure 6, but giving the imaginary part of the frequency instead of its real part. This figure confirms our finding regarding the optimal resolution.

Figure 6. Resolution study for the real part of the frequency for the A/IC-wave solution in quasi-parallel propagation. We keep
![]() $k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\Vert }$
.
$k_{\Vert }$
.

Figure 7. Resolution study for the imaginary part of the frequency for the A/IC-wave solution in quasi-parallel propagation. We keep
![]() $k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\Vert }$
.
$k_{\Vert }$
.
Figures 8 and 9 show the same as figures 6 and 7, but for quasi-perpendicular propagation instead of quasi-parallel propagation. The required resolution is lower in the quasi-perpendicular case than in the quasi-parallel case. The solutions with
![]() $P_{\max ,\Vert \text{p}}=4m_{\text{p}}w_{\text{p}}$
and
$P_{\max ,\Vert \text{p}}=4m_{\text{p}}w_{\text{p}}$
and
![]() $\unicode[STIX]{x0394}w_{j}\leqslant 0.1$
lead to a very good agreement between the PLUME and ALPS solutions.
$\unicode[STIX]{x0394}w_{j}\leqslant 0.1$
lead to a very good agreement between the PLUME and ALPS solutions.

Figure 8. Resolution study for the real part of the frequency for the A/IC-wave solution in quasi-perpendicular propagation. We keep
![]() $k_{\Vert }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\Vert }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\bot }$
.
$k_{\bot }$
.

Figure 9. Resolution study for the imaginary part of the frequency for the A/IC-wave solution in quasi-perpendicular propagation. We keep
![]() $k_{\Vert }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\Vert }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\bot }$
.
$k_{\bot }$
.
A.2 Anisotropic bi-Maxwellian distributions
In addition to our Maxwellian test, we study the dependence of the ALPS solutions on the resolutions for the bi-Maxwellian case with
![]() $T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
as shown in figure 3. Figure 10 compares ALPS solutions for the A/IC instability in quasi-parallel propagation for different values of
$T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
as shown in figure 3. Figure 10 compares ALPS solutions for the A/IC instability in quasi-parallel propagation for different values of
![]() $P_{\max ,\Vert \text{p}}$
and
$P_{\max ,\Vert \text{p}}$
and
![]() $\unicode[STIX]{x0394}w_{j}$
with the solutions from PLUME for the real part of the frequency. Figure 11 compares PLUME and ALPS solutions for the imaginary part of the frequency. The solutions with
$\unicode[STIX]{x0394}w_{j}$
with the solutions from PLUME for the real part of the frequency. Figure 11 compares PLUME and ALPS solutions for the imaginary part of the frequency. The solutions with
![]() $P_{\max ,\Vert \text{p}}=4m_{\text{p}}w_{\Vert \text{p}}$
and
$P_{\max ,\Vert \text{p}}=4m_{\text{p}}w_{\Vert \text{p}}$
and
![]() $\unicode[STIX]{x0394}w_{j}\leqslant 0.05$
lead to a good agreement between PLUME and ALPS in both
$\unicode[STIX]{x0394}w_{j}\leqslant 0.05$
lead to a good agreement between PLUME and ALPS in both
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
and
$\unicode[STIX]{x1D714}_{\text{r}}$
and
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.

Figure 10. Resolution study for the real part of the frequency for the A/IC-instability solution in quasi-parallel propagation. We use a bi-Maxwellian plasma with
![]() $T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. We keep
$T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. We keep
![]() $k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\Vert }$
.
$k_{\Vert }$
.
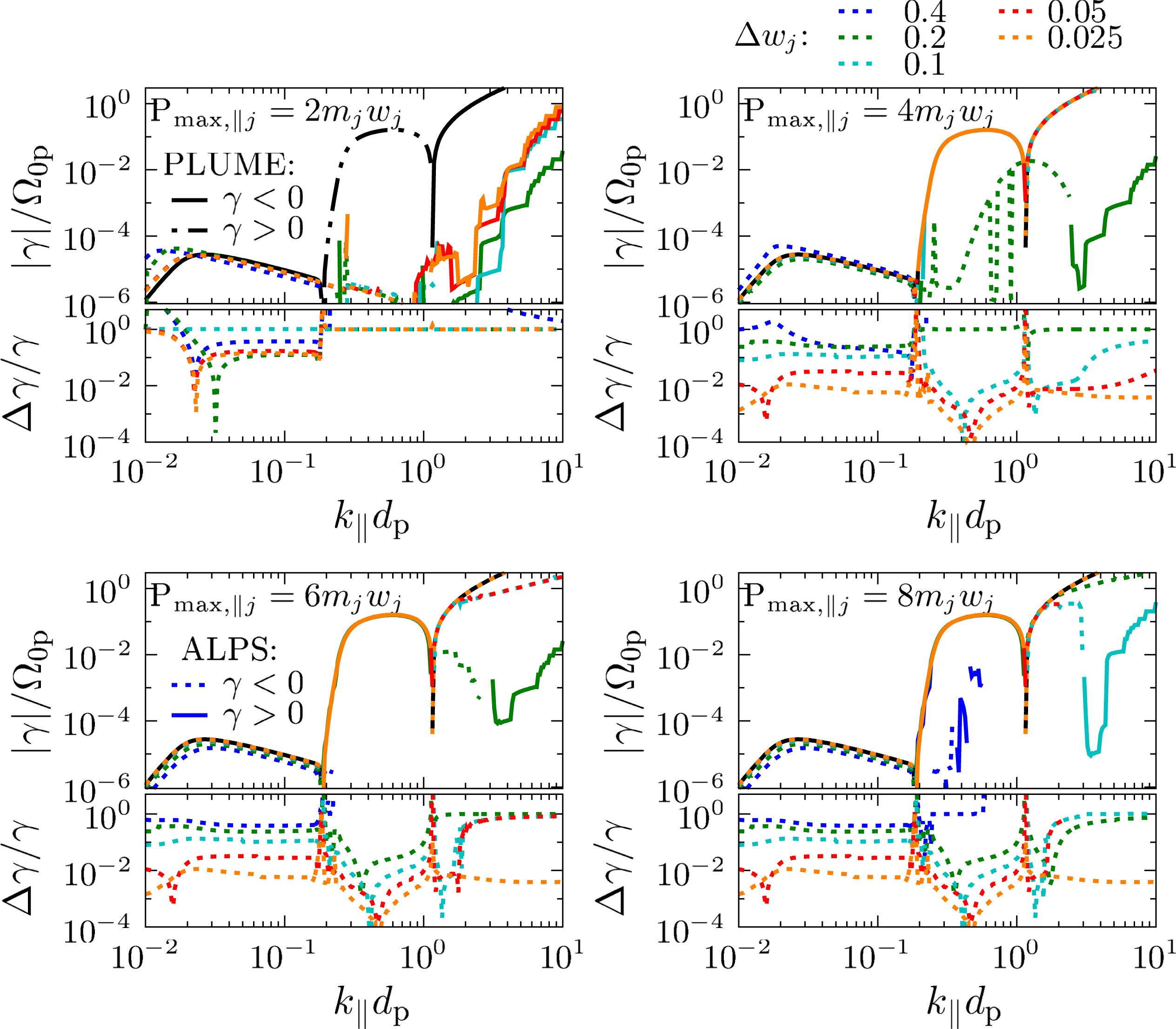
Figure 11. Resolution study for the imaginary part of the frequency for the A/IC-instability solution in quasi-parallel propagation. We use a bi-Maxwellian plasma with
![]() $T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. We keep
$T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. We keep
![]() $k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
$k_{\bot }d_{\text{p}}=10^{-3}$
constant and scan through
![]() $k_{\Vert }$
.
$k_{\Vert }$
.
In figure 12, we study the dependence of the solutions on the resolution for the mirror-mode instability with the same parameters as in figure 3. The correct solution of the mirror-mode instability has
![]() $\unicode[STIX]{x1D714}_{\text{r}}=0$
; however, the ALPS solutions have finite values
$\unicode[STIX]{x1D714}_{\text{r}}=0$
; however, the ALPS solutions have finite values
![]() $\unicode[STIX]{x1D714}_{\text{r}}\neq 0$
. The value of
$\unicode[STIX]{x1D714}_{\text{r}}\neq 0$
. The value of
![]() $\unicode[STIX]{x1D714}_{\text{r}}$
decreases with increasing
$\unicode[STIX]{x1D714}_{\text{r}}$
decreases with increasing
![]() $\unicode[STIX]{x0394}w_{j}$
. As Southwood & Kivelson (Reference Southwood and Kivelson1993) point out, the mirror-mode instability is strongly influenced by particles with
$\unicode[STIX]{x0394}w_{j}$
. As Southwood & Kivelson (Reference Southwood and Kivelson1993) point out, the mirror-mode instability is strongly influenced by particles with
![]() $p_{\Vert }\approx 0$
. The error in frequency
$p_{\Vert }\approx 0$
. The error in frequency
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{\text{r}}$
is determined by the resolution of the momentum grid around
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{\text{r}}$
is determined by the resolution of the momentum grid around
![]() $p_{\Vert }=0$
, where
$p_{\Vert }=0$
, where
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{\text{r}}\sim k_{\Vert }w_{j}\,\unicode[STIX]{x0394}w_{j}$
. Figure 13 shows the comparison of the imaginary part of the mirror-mode solutions. Like in the case of the A/IC instability, a resolution with
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{\text{r}}\sim k_{\Vert }w_{j}\,\unicode[STIX]{x0394}w_{j}$
. Figure 13 shows the comparison of the imaginary part of the mirror-mode solutions. Like in the case of the A/IC instability, a resolution with
![]() $P_{\max ,\Vert p}=4m_{\text{p}}w_{\Vert \text{p}}$
and
$P_{\max ,\Vert p}=4m_{\text{p}}w_{\Vert \text{p}}$
and
![]() $\unicode[STIX]{x0394}w_{j}\leqslant 0.05$
leads to a good agreement between PLUME and ALPS. We note that there is a non-monotonic behaviour in the accuracy of the solutions in some cases (see, for example, the solutions for
$\unicode[STIX]{x0394}w_{j}\leqslant 0.05$
leads to a good agreement between PLUME and ALPS. We note that there is a non-monotonic behaviour in the accuracy of the solutions in some cases (see, for example, the solutions for
![]() $\unicode[STIX]{x0394}w_{j}=0.2$
,
$\unicode[STIX]{x0394}w_{j}=0.2$
,
![]() $\unicode[STIX]{x0394}w_{j}=0.1$
, and
$\unicode[STIX]{x0394}w_{j}=0.1$
, and
![]() $\unicode[STIX]{x0394}w_{j}=0.05$
in figure 13). This illustrates that an increase in resolution sometimes causes the code to lose a solution that it successfully finds at lower resolutions. Since this numerical problem eventually resolves itself after increasing the resolution further, we recommend applying a higher resolution whenever the code loses a solution.
$\unicode[STIX]{x0394}w_{j}=0.05$
in figure 13). This illustrates that an increase in resolution sometimes causes the code to lose a solution that it successfully finds at lower resolutions. Since this numerical problem eventually resolves itself after increasing the resolution further, we recommend applying a higher resolution whenever the code loses a solution.

Figure 12. Resolution study for the real part of the frequency for the mirror-mode-instability solution. We use a bi-Maxwellian plasma with
![]() $T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. We keep
$T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. We keep
![]() $\unicode[STIX]{x1D703}=75^{\circ }$
constant and scan through
$\unicode[STIX]{x1D703}=75^{\circ }$
constant and scan through
![]() $|\boldsymbol{k}|$
.
$|\boldsymbol{k}|$
.

Figure 13. Resolution study for the imaginary part of the frequency for the mirror-mode-instability solution. We use a bi-Maxwellian plasma with
![]() $T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. We keep
$T_{\bot \text{p}}/T_{\Vert \text{p}}=3$
. We keep
![]() $\unicode[STIX]{x1D703}=75^{\circ }$
constant and scan through
$\unicode[STIX]{x1D703}=75^{\circ }$
constant and scan through
![]() $|\boldsymbol{k}|$
.
$|\boldsymbol{k}|$
.
Appendix B. Levenberg–Marquardt fit
For the hybrid analytic continuation, ALPS fits the
![]() $f_{0}$
table with a combination of pre-described algebraic expressions as described in § 3.2. We employ a Levenberg–Marquardt algorithm (Levenberg Reference Levenberg1944; Marquardt Reference Marquardt1963) to fit the distribution functions in
$f_{0}$
table with a combination of pre-described algebraic expressions as described in § 3.2. We employ a Levenberg–Marquardt algorithm (Levenberg Reference Levenberg1944; Marquardt Reference Marquardt1963) to fit the distribution functions in
![]() $p_{\Vert }$
with a superposition of an arbitrary number of Maxwellian distributions,
$p_{\Vert }$
with a superposition of an arbitrary number of Maxwellian distributions,
![]() $\unicode[STIX]{x1D705}$
-distributions and Jüttner distributions. The user can freely choose the number of fits and their superposition. We evaluate different fit parameters for each given value of
$\unicode[STIX]{x1D705}$
-distributions and Jüttner distributions. The user can freely choose the number of fits and their superposition. We evaluate different fit parameters for each given value of
![]() $p_{\bot }$
. We define the Maxwellian fitting function as
$p_{\bot }$
. We define the Maxwellian fitting function as
where
![]() $u_{k}$
are the fit parameters,
$u_{k}$
are the fit parameters,
![]() $y$
is a constant user-defined parameter and
$y$
is a constant user-defined parameter and
![]() $\hat{p}_{\bot }$
and
$\hat{p}_{\bot }$
and
![]() $\hat{p}_{\Vert }$
are the normalised perpendicular and parallel momenta. The parameter
$\hat{p}_{\Vert }$
are the normalised perpendicular and parallel momenta. The parameter
![]() $y$
compensates the otherwise strong
$y$
compensates the otherwise strong
![]() $p_{\bot }$
-dependence of
$p_{\bot }$
-dependence of
![]() $u_{1}$
, making the fit more reliable. It is constant for all
$u_{1}$
, making the fit more reliable. It is constant for all
![]() $p_{\bot }$
. We choose this expression rather than a fit in
$p_{\bot }$
. We choose this expression rather than a fit in
![]() $p_{\bot }$
since it provides a greater flexibility in the
$p_{\bot }$
since it provides a greater flexibility in the
![]() $p_{\bot }$
-domain compared to a two-dimensional fit in
$p_{\bot }$
-domain compared to a two-dimensional fit in
![]() $p_{\bot }$
and
$p_{\bot }$
and
![]() $p_{\Vert }$
. The best choice for
$p_{\Vert }$
. The best choice for
![]() $y$
is
$y$
is
![]() $\unicode[STIX]{x1D6FD}_{\bot j}m_{\text{p}}/m_{j}$
. The standard normalisation in ALPS uses
$\unicode[STIX]{x1D6FD}_{\bot j}m_{\text{p}}/m_{j}$
. The standard normalisation in ALPS uses
![]() $\hat{p}_{\bot }=p_{\bot }/m_{\text{p}}v_{\text{A}}$
and
$\hat{p}_{\bot }=p_{\bot }/m_{\text{p}}v_{\text{A}}$
and
![]() $\hat{p}_{\Vert }=p_{\Vert }/m_{\text{p}}v_{\text{A}}$
. In cases with
$\hat{p}_{\Vert }=p_{\Vert }/m_{\text{p}}v_{\text{A}}$
. In cases with
![]() $\unicode[STIX]{x1D705}$
-distributed plasma components, we use
$\unicode[STIX]{x1D705}$
-distributed plasma components, we use
In cases with Jüttner-distributed plasma components, we use
In this case, the best choice for
![]() $y$
is
$y$
is
![]() $2c^{2}/w_{j}^{2}$
. These fitting relations are easily extendable by the user to cover more general functions as needed.
$2c^{2}/w_{j}^{2}$
. These fitting relations are easily extendable by the user to cover more general functions as needed.
We denote the discretised
![]() $f_{0}$
table of species
$f_{0}$
table of species
![]() $j$
at constant
$j$
at constant
![]() $p_{\bot }$
as
$p_{\bot }$
as
![]() $\hat{f}_{i,j}(\hat{p}_{\Vert ,i})$
, the discrete steps in
$\hat{f}_{i,j}(\hat{p}_{\Vert ,i})$
, the discrete steps in
![]() $\hat{p}_{\Vert }$
as
$\hat{p}_{\Vert }$
as
![]() $\hat{p}_{\Vert ,i}$
, the vector of all fit parameters as
$\hat{p}_{\Vert ,i}$
, the vector of all fit parameters as
![]() $\boldsymbol{u}$
and the sum of all fit functions as
$\boldsymbol{u}$
and the sum of all fit functions as
![]() $F(\hat{p}_{\Vert })$
. In the Jüttner-distributed cases, the coordinates are replaced with
$F(\hat{p}_{\Vert })$
. In the Jüttner-distributed cases, the coordinates are replaced with
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\bar{p}_{\Vert }$
accordingly. We define the residuals as
$\bar{p}_{\Vert }$
accordingly. We define the residuals as
![]() $s_{i}\equiv \hat{f}_{i,j}-F(\hat{p}_{\Vert ,i})$
and define
$s_{i}\equiv \hat{f}_{i,j}-F(\hat{p}_{\Vert ,i})$
and define
![]() $C\equiv \sum _{i}s_{i}^{2}$
. We denote the Jacobian of
$C\equiv \sum _{i}s_{i}^{2}$
. We denote the Jacobian of
![]() $\hat{\boldsymbol{f}}_{j}$
with respect to
$\hat{\boldsymbol{f}}_{j}$
with respect to
![]() $\boldsymbol{u}$
as
$\boldsymbol{u}$
as
![]() $\unicode[STIX]{x1D645}$
. We use a superposition of analytical expressions for the Jacobian based on the given form of
$\unicode[STIX]{x1D645}$
. We use a superposition of analytical expressions for the Jacobian based on the given form of
![]() $F(\hat{p}_{\Vert })$
. The Levenberg–Marquardt algorithm uses an iterative step to update
$F(\hat{p}_{\Vert })$
. The Levenberg–Marquardt algorithm uses an iterative step to update
![]() $\boldsymbol{u}$
of the form
$\boldsymbol{u}$
of the form
where
![]() $\unicode[STIX]{x1D706}$
is a user-defined scalar. For the matrix inversion in (B 4), we use the
$\unicode[STIX]{x1D706}$
is a user-defined scalar. For the matrix inversion in (B 4), we use the
![]() $\unicode[STIX]{x1D647}\unicode[STIX]{x1D650}$
-factorisation. Then we calculate the residuals
$\unicode[STIX]{x1D647}\unicode[STIX]{x1D650}$
-factorisation. Then we calculate the residuals
![]() $\boldsymbol{s}_{\text{new}}$
based on
$\boldsymbol{s}_{\text{new}}$
based on
![]() $\boldsymbol{u}_{\text{new}}$
and determine
$\boldsymbol{u}_{\text{new}}$
and determine
![]() $C_{\text{new}}=|\boldsymbol{s}_{\text{new}}|^{2}$
. If
$C_{\text{new}}=|\boldsymbol{s}_{\text{new}}|^{2}$
. If
![]() $C_{\text{new}}\leqslant C$
, we set
$C_{\text{new}}\leqslant C$
, we set
![]() $\boldsymbol{u}$
to
$\boldsymbol{u}$
to
![]() $\boldsymbol{u}_{\text{new}}$
, reduce
$\boldsymbol{u}_{\text{new}}$
, reduce
![]() $\unicode[STIX]{x1D706}$
by a constant factor
$\unicode[STIX]{x1D706}$
by a constant factor
![]() $\unicode[STIX]{x1D706}_{\text{f}}$
(user-defined, standard value is 10) and repeat the procedure. If
$\unicode[STIX]{x1D706}_{\text{f}}$
(user-defined, standard value is 10) and repeat the procedure. If
![]() $C_{\text{new}}>C$
, we discard
$C_{\text{new}}>C$
, we discard
![]() $u_{\text{new}}$
, increase
$u_{\text{new}}$
, increase
![]() $\unicode[STIX]{x1D706}$
by the constant factor
$\unicode[STIX]{x1D706}$
by the constant factor
![]() $\unicode[STIX]{x1D706}_{\text{f}}$
and repeat the procedure. In this way, we iteratively determine the fit parameters
$\unicode[STIX]{x1D706}_{\text{f}}$
and repeat the procedure. In this way, we iteratively determine the fit parameters
![]() $\boldsymbol{u}$
until the fit converges (i.e.
$\boldsymbol{u}$
until the fit converges (i.e.
![]() $C\leqslant \unicode[STIX]{x1D716}$
with a user-defined
$C\leqslant \unicode[STIX]{x1D716}$
with a user-defined
![]() $\unicode[STIX]{x1D716}$
), or until the number of iterations reaches a user-defined maximum value. ALPS writes the fitted distribution into a separate output file so that a direct comparison with the original input distribution is possible.
$\unicode[STIX]{x1D716}$
), or until the number of iterations reaches a user-defined maximum value. ALPS writes the fitted distribution into a separate output file so that a direct comparison with the original input distribution is possible.
Appendix C. The smoothed thin-plate spline interpolation
Spacecraft or other plasma data are typically not available on a dense Cartesian grid like the grid required for an
![]() $f_{0}$
table in ALPS. Therefore, our code includes an interpolation algorithm that fills gaps between data points. ALPS uses the same interpolation algorithm to create an equidistant grid in
$f_{0}$
table in ALPS. Therefore, our code includes an interpolation algorithm that fills gaps between data points. ALPS uses the same interpolation algorithm to create an equidistant grid in
![]() $(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
space after the coordinate transformation in cases with relativistic poles. We use a polyharmonic-spline interpolation with the radial basis function of a thin-plate spline with smoothing (Powell Reference Powell, Dikshit and Micchelli1994; Donato & Belongie Reference Donato and Belongie2002). For each species, we begin with the ‘coarse’ distribution function
$(\unicode[STIX]{x1D6E4},\bar{p}_{\Vert })$
space after the coordinate transformation in cases with relativistic poles. We use a polyharmonic-spline interpolation with the radial basis function of a thin-plate spline with smoothing (Powell Reference Powell, Dikshit and Micchelli1994; Donato & Belongie Reference Donato and Belongie2002). For each species, we begin with the ‘coarse’ distribution function
![]() $\hat{f}_{\text{c},\unicode[STIX]{x1D707}}$
which is given by
$\hat{f}_{\text{c},\unicode[STIX]{x1D707}}$
which is given by
![]() $N_{\text{c}}$
data points (index
$N_{\text{c}}$
data points (index
![]() $\unicode[STIX]{x1D707}=1\ldots N_{\text{c}}$
) with the associated coarse momentum coordinates
$\unicode[STIX]{x1D707}=1\ldots N_{\text{c}}$
) with the associated coarse momentum coordinates
![]() $\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}}$
and
$\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}}$
and
![]() $\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}}$
. The set
$\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}}$
. The set
![]() $(\hat{f}_{\text{c},\unicode[STIX]{x1D707}},\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}},\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}})$
forms one data point. The coarse grid is typically not equally distributed in momentum space.
$(\hat{f}_{\text{c},\unicode[STIX]{x1D707}},\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}},\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}})$
forms one data point. The coarse grid is typically not equally distributed in momentum space.
For each species, the ‘fine’ grid of momentum coordinates is given by
![]() $\hat{p}_{\bot ,i,k}$
and
$\hat{p}_{\bot ,i,k}$
and
![]() $\hat{p}_{\Vert ,i,k}$
with
$\hat{p}_{\Vert ,i,k}$
with
![]() $i=1\ldots N_{\bot }$
and
$i=1\ldots N_{\bot }$
and
![]() $k=1\ldots N_{\Vert }$
(and correspondingly in the coordinates
$k=1\ldots N_{\Vert }$
(and correspondingly in the coordinates
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\bar{p}_{\Vert }$
for cases with relativistic poles). The fine grid corresponds to the actual
$\bar{p}_{\Vert }$
for cases with relativistic poles). The fine grid corresponds to the actual
![]() $f_{0}$
table to be used as input in ALPS. The goal of our interpolation is to find the value of the distribution function
$f_{0}$
table to be used as input in ALPS. The goal of our interpolation is to find the value of the distribution function
![]() $\hat{f}_{i,k}$
on all grid points
$\hat{f}_{i,k}$
on all grid points
![]() $(i,k)$
. We define the vectors
$(i,k)$
. We define the vectors
![]() $\boldsymbol{w}=(w_{1},\ldots ,w_{N_{\text{c}}})$
,
$\boldsymbol{w}=(w_{1},\ldots ,w_{N_{\text{c}}})$
,
![]() $\boldsymbol{c}=(c_{1},c_{2},c_{3})$
,
$\boldsymbol{c}=(c_{1},c_{2},c_{3})$
,
![]() $\hat{\boldsymbol{f}}_{\text{c}}=(\hat{f}_{\text{c},1},\ldots ,\hat{f}_{\text{c},N_{\text{c}}})$
and
$\hat{\boldsymbol{f}}_{\text{c}}=(\hat{f}_{\text{c},1},\ldots ,\hat{f}_{\text{c},N_{\text{c}}})$
and
![]() $\mathbf{0}=(0,0,0)$
. We furthermore define the matrix
$\mathbf{0}=(0,0,0)$
. We furthermore define the matrix
where
![]() $r\equiv \sqrt{(\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}}-\hat{p}_{\bot \text{c},\unicode[STIX]{x1D708}})^{2}+(\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}}-\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D708}})^{2}}$
. We also define the
$r\equiv \sqrt{(\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}}-\hat{p}_{\bot \text{c},\unicode[STIX]{x1D708}})^{2}+(\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}}-\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D708}})^{2}}$
. We also define the
![]() $(N_{\text{c}}\times 3)$
matrix
$(N_{\text{c}}\times 3)$
matrix
![]() $\unicode[STIX]{x1D64B}$
. Its
$\unicode[STIX]{x1D64B}$
. Its
![]() $\unicode[STIX]{x1D707}$
th row is given by
$\unicode[STIX]{x1D707}$
th row is given by
![]() $(1,\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}},\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}})$
. The thin-plate spline interpolation requires us to solve the non-homogeneous linear system of equations
$(1,\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}},\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}})$
. The thin-plate spline interpolation requires us to solve the non-homogeneous linear system of equations
for the vectors
![]() $\boldsymbol{w}$
and
$\boldsymbol{w}$
and
![]() $\boldsymbol{c}$
.
$\boldsymbol{c}$
.
![]() $\unicode[STIX]{x1D6FC}$
is a user-defined smoothing parameter (
$\unicode[STIX]{x1D6FC}$
is a user-defined smoothing parameter (
![]() $\unicode[STIX]{x1D6FC}=0$
forces the fine grid to run through all points of the coarse grid), and
$\unicode[STIX]{x1D6FC}=0$
forces the fine grid to run through all points of the coarse grid), and
![]() $\mathbf{1}$
is the
$\mathbf{1}$
is the
![]() $(N_{\text{c}}\times N_{\text{c}})$
unit matrix. The interpolation is then given by
$(N_{\text{c}}\times N_{\text{c}})$
unit matrix. The interpolation is then given by
where
![]() $R_{i,k}^{\unicode[STIX]{x1D707}}\equiv \sqrt{(\hat{p}_{\bot ,i,k}-\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}})^{2}+(\hat{p}_{\Vert ,i,k}-\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}})^{2}}$
. The numerically expensive part of the interpolation is the solution of (C 2). Since
$R_{i,k}^{\unicode[STIX]{x1D707}}\equiv \sqrt{(\hat{p}_{\bot ,i,k}-\hat{p}_{\bot \text{c},\unicode[STIX]{x1D707}})^{2}+(\hat{p}_{\Vert ,i,k}-\hat{p}_{\Vert \text{c},\unicode[STIX]{x1D707}})^{2}}$
. The numerically expensive part of the interpolation is the solution of (C 2). Since
![]() $\unicode[STIX]{x1D612}_{11}=0$
, a direct
$\unicode[STIX]{x1D612}_{11}=0$
, a direct
![]() $\unicode[STIX]{x1D647}\unicode[STIX]{x1D650}$
-factorisation is not possible. Therefore, we apply a
$\unicode[STIX]{x1D647}\unicode[STIX]{x1D650}$
-factorisation is not possible. Therefore, we apply a
![]() $\unicode[STIX]{x1D647}\unicode[STIX]{x1D650}$
-factorisation algorithm with partial pivoting through row permutations until
$\unicode[STIX]{x1D647}\unicode[STIX]{x1D650}$
-factorisation algorithm with partial pivoting through row permutations until
![]() $\unicode[STIX]{x1D612}_{11}\neq 0$
.
$\unicode[STIX]{x1D612}_{11}\neq 0$
.