No CrossRef data available.
Published online by Cambridge University Press: 14 November 2019
We derive a dispersion relation for the damping of acoustic waves in equi-molar deuterium–tritium (DT) gas due to radiation coupling and electron thermal conduction and discuss its significance for inertial confinement fusion (ICF) targets with high-Z shells surrounding a central DT fuel region. As the shell implodes around DT fuel in such a target, shocks and waves are transmitted through the DT gas. If the shell is perturbed due to drive non-uniformity or manufacturing imperfection, these shocks and waves may be perturbed as well, and can potentially re-perturb the shell. This can complicate calculation of shell stability and implosion asymmetry and in general make the target less robust against implosion non-uniformity. Damping of perturbations in DT gas can alleviate these complications. Also, damping of low-order modes, which is primarily due to radiation coupling, can drive the DT gas to an isobaric and isothermal ‘equilibrium’ configuration during ignition. We find that for the range of common ignition temperatures in targets with high-Z shells,  $2.5\lesssim T_{ig}\lesssim 3.5$ keV, damping of low-order modes is significant for areal densities (
$2.5\lesssim T_{ig}\lesssim 3.5$ keV, damping of low-order modes is significant for areal densities (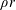 $\unicode[STIX]{x1D70C}r$) in the broad range of
$\unicode[STIX]{x1D70C}r$) in the broad range of 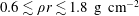 $0.6\lesssim \unicode[STIX]{x1D70C}r\lesssim 1.8~\text{g}~\text{cm}^{-2}$. This suggests it is advantageous to design these targets to achieve areal densities at ignition within this range. Furthermore, we derive a simple constraint between areal density and temperature,
$0.6\lesssim \unicode[STIX]{x1D70C}r\lesssim 1.8~\text{g}~\text{cm}^{-2}$. This suggests it is advantageous to design these targets to achieve areal densities at ignition within this range. Furthermore, we derive a simple constraint between areal density and temperature, 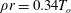 $\unicode[STIX]{x1D70C}r=0.34T_{o}$ where
$\unicode[STIX]{x1D70C}r=0.34T_{o}$ where  $T_{o}$ is in keV, such that DT gas undergoing equilibrium ignition is optimally robust against non-uniformity.
$T_{o}$ is in keV, such that DT gas undergoing equilibrium ignition is optimally robust against non-uniformity.