Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Todo, Y
Sato, M
Wang, Hao
Idouakass, M
and
Seki, R
2021.
Magnetohydrodynamic hybrid simulation model with kinetic thermal ions and energetic particles .
Plasma Physics and Controlled Fusion,
Vol. 63,
Issue. 7,
p.
075018.
Ichiguchi, K.
Suzuki, Y.
Todo, Y.
Sakakibara, S.
Ida, K.
Takemura, Y.
Sato, M.
Sugiyama, L.E.
and
Carreras, B.A.
2021.
Non-resonant global mode in LHD partial collapse with net toroidal current.
Nuclear Fusion,
Vol. 61,
Issue. 12,
p.
126056.
Idouakass, M.
Todo, Y.
Wang, H.
Wang, J.
Seki, R.
and
Sato, M.
2021.
Precession drift reversal and rapid transport of trapped energetic particles due to an energetic particle driven instability in the Large Helical Device.
Physics of Plasmas,
Vol. 28,
Issue. 8,
Sato, M.
and
Todo, Y.
2021.
Kinetic thermal ion effects on maintaining high beta plasmas above the Mercier criterion in the Large Helical Device.
Nuclear Fusion,
Vol. 61,
Issue. 11,
p.
116012.
Wang, Hao
Todo, Yasushi
Huang, Jie
Suzuki, Yasuhiro
Shimizu, Akihiro
Ogawa, Kunihiro
Wang, Xianqu
and
Adulsiriswad, Panith
2022.
Simulations of energetic particle driven instabilities in CFQS.
Nuclear Fusion,
Vol. 62,
Issue. 10,
p.
106010.
Liu, Chang
Jardin, Stephen C.
Bao, Jian
Gorelenkov, Nikolai
Brennan, Dylan P.
Yang, James
and
Podesta, Mario
2022.
Thermal ion kinetic effects and Landau damping in fishbone modes.
Journal of Plasma Physics,
Vol. 88,
Issue. 6,
TODO, Yasushi
MIURA, Hideaki
TOIDA, Mieko
ISHIZAKI, Ryuichi
SATO, Masahiko
WANG, Hao
SEKI, Ryosuke
WANG, Jialei
IDOUAKASS, Malik
ADULSIRISWAD, Panith
MIZUGUCHI, Naoki
YAMAMOTO, Takashi
and
SUGAMA, Hideo
2023.
Research Plan of Complex Global Simulation Unit.
Plasma and Fusion Research,
Vol. 18,
Issue. 0,
p.
2503067.
Varela, J.
Nagaoka, K.
Takemura, Y.
Watanabe, K. Y.
Ida, K.
Yoshinuma, M.
Nagasaki, K.
Cappa, A.
Sharapov, S.
Spong, D. A.
Garcia, L.
Ghai, Y.
and
Ortiz, J.
2024.
MHD stability trends and improved performance of LHD inward-shifted configurations: The role of the neutral beam current drive and thermal plasma density.
Physics of Plasmas,
Vol. 31,
Issue. 8,
Sato, M.
Todo, Y.
Aiba, N.
and
Takechi, M.
2024.
Kinetic-magnetohydrodynamic hybrid simulation of infernal modes in circular tokamak plasmas with effects of kinetic thermal ions.
Nuclear Fusion,
Vol. 64,
Issue. 7,
p.
076021.
Sun, Yingtao
Wei, Zhenhua
Zhou, Jianfeng
Mao, Aiqin
and
Bian, Di
2024.
Modification of magnetorheological fluid and its compatibility with metal skeleton: Insights from multi-body dissipative particle dynamics simulations and experimental study.
Physics of Fluids,
Vol. 36,
Issue. 3,
Wang (王灏), Hao
Lauber, Philipp W.
Todo (藤堂泰), Yasushi
Suzuki (鈴木康浩), Yasuhiro
Li (李瀚政), Hanzheng
Wang (王佳磊), Jialei
and
Wei (魏士朝), Shizhao
2024.
Nonlinear excitation of energetic particle driven geodesic acoustic mode by Alfvén instability in ASDEX-Upgrade Tokamak.
Nuclear Fusion,
Vol. 64,
Issue. 7,
p.
076015.
Ortiz, J.
Varela, J.
Herrera Quesada, L.
Pons-Villalonga, P.
Cappa, A.
Losada, U.
Papoušek, F.
van Milligen, B. Ph.
Garcia, L.
Spong, D. A.
Ghai, Y.
Ochando, M. A.
and
Hidalgo, C.
2025.
Analysis of the HAE activity in the TJ-II stellarator using a Landau closure model.
Physics of Plasmas,
Vol. 32,
Issue. 7,
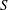 $S$ using numerical simulations based on the kinetic MHD model with kinetic thermal ions where the beta is the ratio of the plasma pressure to the magnetic pressure. It is found that the dependence of the linear growth rate of the resistive ballooning modes on the
$S$ using numerical simulations based on the kinetic MHD model with kinetic thermal ions where the beta is the ratio of the plasma pressure to the magnetic pressure. It is found that the dependence of the linear growth rate of the resistive ballooning modes on the 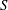 $S$ number changes from
$S$ number changes from 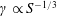 $\unicode[STIX]{x1D6FE}\propto S^{-1/3}$ to
$\unicode[STIX]{x1D6FE}\propto S^{-1/3}$ to 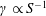 $\unicode[STIX]{x1D6FE}\propto S^{-1}$ by the kinetic thermal ion effects so that the resistive ballooning modes are significantly suppressed as the
$\unicode[STIX]{x1D6FE}\propto S^{-1}$ by the kinetic thermal ion effects so that the resistive ballooning modes are significantly suppressed as the 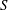 $S$ number increases. For a high
$S$ number increases. For a high 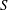 $S$ number comparable to experimental values, the most unstable modes are interchange modes. The kinetic thermal ion effects change the most unstable interchange mode from the ideal mode to the resistive mode. This transition of the interchange modes by kinetic thermal ion effects is consistent with the shift of the marginal stability boundary for the ideal interchange modes observed in the LHD experiments.
$S$ number comparable to experimental values, the most unstable modes are interchange modes. The kinetic thermal ion effects change the most unstable interchange mode from the ideal mode to the resistive mode. This transition of the interchange modes by kinetic thermal ion effects is consistent with the shift of the marginal stability boundary for the ideal interchange modes observed in the LHD experiments.
