No CrossRef data available.
Article contents
Driving magnetic turbulence using flux ropes in a moderate guide field linear system
Published online by Cambridge University Press: 09 November 2017
Abstract
We present a series of experiments on novel, line-tied plasma geometries as a study of the generation of chaos and turbulence in line-tied systems. Plasma production and the injection scale for magnetic energy is provided by spatially discrete plasma guns that inject both plasma and current. The guns represent a technique for controlling the injection scale of magnetic energy. A two-dimensional (2-D) array of magnetic probes provides spatially resolved time histories of the magnetic fluctuations at a single cross-section of the experimental cylinder, allowing simultaneous spatial measurements of chaotic and turbulent behaviour. The first experiment shows chaotic fluctuations and self-organization in a hollow-current line-tied screw pinch. These dynamics is modulated primarily by the applied magnetic field and weakly by the plasma current and safety factor. The second experiment analyses the interactions of multiple line-tied flux ropes. The flux ropes all exhibit chaotic behaviour, and under certain conditions develop an inverse cascade to larger scales and a turbulent inertial range with magnetic energy ( 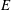 $E$ ) related to perpendicular wave number (
$E$ ) related to perpendicular wave number ( 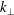 $k_{\bot }$ ) as
$k_{\bot }$ ) as 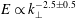 $E\propto k_{\bot }^{-2.5\pm 0.5}$ .
$E\propto k_{\bot }^{-2.5\pm 0.5}$ .
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2017

