Article contents
Virtual machine concept applied to uncertainties estimation in instrumented indentation testing
Published online by Cambridge University Press: 29 July 2019
Abstract
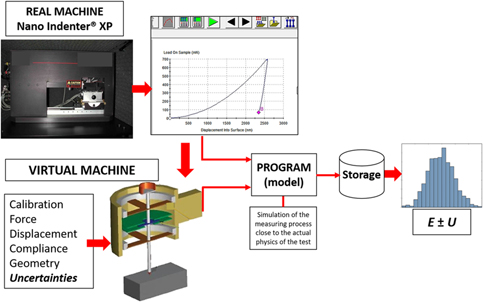
The basis of the virtual machine concept, which is commonly used in coordinate measuring machines, was implemented to determine more realistic uncertainties on the estimation of the elastic modulus obtained from nanoindentation tests. The methodology is based on a mathematical model applied to simulate the testing process and to evaluate the uncertainties through Monte Carlo simulations whose application depends on the studied system (instrument, material, scale, etc.). The methodology was applied to the study of fused silica (FQ) and steel samples tested in a nanoindentation system. The results revealed that the most relevant sources of uncertainty are related to the calibration procedure, particularly to the elastic modulus of the calibration material, and to the contact depth estimation; however, the relevance of the uncertainties is system dependent. This work represents a first insight for a deeper consideration of the uncertainties in instrumented indentation testing.
Information
- Type
- Article
- Information
- Copyright
- Copyright © Materials Research Society 2019
References
- 8
- Cited by

