Article contents
Piezoelectric polymer thin films with architected cuts
Published online by Cambridge University Press: 14 February 2018
Abstract
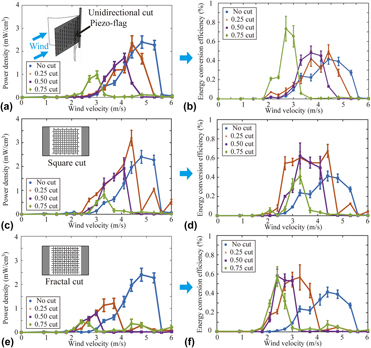
Introducing architected cuts is an attractive and simple approach to tune mechanical behaviors of planar materials like thin films for desirable or enhanced mechanical performance. However, little has been studied on the effects of architected cuts on functional materials like piezoelectric materials. We investigated how architected cut patterns affect mechanical and piezoelectric properties of polyvinylidene fluoride thin films by numerical, experimental, and analytical studies. Our results show that thin films with architected cuts can provide desired mechanical features like enhanced compliance, stretchability, and controllable Poisson’s ratio and resonance frequency, while maintaining piezoelectric performance under static loadings. Moreover, we could observe maximum ∼30% improvement in piezoelectric conversion efficiency under dynamic loadings and harvest energy from low frequency (<100 Hz) mechanical signals or low velocity (<5 m/s) winds, which are commonly existing in ambient environment. Using architected cuts doesn't require changing the material or overall dimensions, making it attractive for applications in self-powered devices with design constraints.
Keywords
Information
- Type
- Invited Articles
- Information
- Journal of Materials Research , Volume 33 , Issue 3: Focus Issue: Architected Materials , 14 February 2018 , pp. 330 - 342
- Copyright
- Copyright © Materials Research Society 2018
Footnotes
Contributing Editor: Christopher Spadaccini
References
REFERENCES
A correction has been issued for this article:
- 15
- Cited by
Linked content
Please note a has been issued for this article.

