Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-12T12:51:33.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Performance optimization of a thermoelectric generator element with linear, spatial material profiles in a one-dimensional setup

Published online by Cambridge University Press:  29 June 2011

Knud Zabrocki ,
Eckhard Müller ,
Wolfgang Seifert  and
Steffen Trimper
Knud Zabrocki*
Affiliation:
Institute of Materials Research, German Aerospace Center (DLR), D-51170 Köln, Germany
Eckhard Müller
Affiliation:
Institute of Materials Research, German Aerospace Center (DLR), D-51170 Köln, Germany
Wolfgang Seifert
Affiliation:
Institute of Physics, University Halle-Wittenberg, D-06099 Halle, Germany
Steffen Trimper
Affiliation:
Institute of Physics, University Halle-Wittenberg, D-06099 Halle, Germany
*
a)Address all correspondence to this author. e-mail: knud.zabrocki@dlr.de
Get access

Abstract

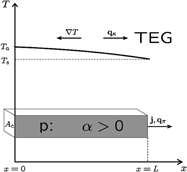
Graded and segmented thermoelectric elements are studied in order to improve the performance of thermogenerators that are exposed to a large temperature difference. The linear thermodynamics of irreversible processes is extended by assuming spatially dependent material parameters like the Seebeck coefficient, the electrical and thermal conductivities. For the particular case in which these transport coefficients exhibit a constant gradient, we present an analytical solution of the one-dimensional thermal energy balance in terms of Bessel functions. Given linear spatial material profiles, we discuss the optimization of performance parameters like the electrical power Pel and the efficiency η of a graded thermogenerator element of fixed length and fixed boundary temperatures. The results are compared with the constant properties model, i.e., physically and chemically homogeneous material, as a suitable reference for performance evaluation.

Keywords

thermoelectricity
Type
Articles
Information
Journal of Materials Research , Volume 26 , Issue 15: Focus Issue: Advances in Thermoelectric Materials , 14 August 2011 , pp. 1963 - 1974
Copyright
Copyright © Materials Research Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Behnia, K., Jaccard, D., and Flouquet, J.: On the thermoelectricity of correlated electrons in the zero-temperature limit. J. Phys. Condens. Matter 16, 5187 (2004).CrossRefGoogle Scholar
2.Behnia, K.: The Nernst effect and the boundaries of the Fermi liquid picture. J. Phys. Condens. Matter 21, 113101 (2009).CrossRefGoogle ScholarPubMed
3.Kovalev, A.A. and Tserkovnyak, Y.: Thermoelectric spin transfer in textured magnets. Phys. Rev. B 80, 100408 (2009).CrossRefGoogle Scholar
4.Zhu, L., Ma, R., Sheng, L., Liu, M., and Sheng, D.-N.: Universal thermoelectric effect of dirac fermions in graphene. Phys. Rev. Lett. 104, 076804 (2010).CrossRefGoogle ScholarPubMed
5.Kuznetsov, V.L.: Functionally graded materials for thermoelectric applications, in CRC Handbook of Thermoelectrics: Macro to Nano (Taylor & Francis, Boca Raton, FL, 2006; chap. 28).Google Scholar
6.Müller, E., Zabrocki, K., Goupil, C., Snyder, G.J., and Seifert, W.: Functionally graded thermoelectric generator and cooler elements. in CRC Handbook of Thermoelectrics: Thermoelectrics and Its Energy Harvesting (Rowe, D.M., ed., RC, Boca Raton, FL, 2011).Google Scholar
7.Altenkirch, E.: Über den Nutzeffekt der Thermosäulen. Phys. Z. 10, 560–580, (1909).Google Scholar
8.Altenkirch, E.: Elektrothermische Kälteerzeugung und reversible elektrische Heizung. Phys. Z. 12, 920–924 (1911).Google Scholar
9.Ioffe, A.F.: Semiconductor Thermoelements and Thermoelectric Cooling (Infosearch, Ltd., London, 1957).Google Scholar
10.Jonson, M. and Mahan, G.D.: Mott’s formula for the thermopower and the Wiedemann–Franz law. Phys. Rev. B 21, 4223–4229 (1980).CrossRefGoogle Scholar
11.Wiedemann, G. and Franz, R.: Ueber die Wärme-Leitungsfähigkeit der Metalle. Ann. Phys. 89, 497–531 (1953).Google Scholar
12.Ashcroft, N.W. and Mermin, N.D.: Solid State Physics (Saunders College, Philadelphia, PA, 1976).Google Scholar
13.Telkes, M.: Westinghouse Research Report R-94264-B (1938).Google Scholar
14.Wood, C.: Materials for thermoelectric energy conversion. Reports Progr. Phys. 51, 459–539 (1988).CrossRefGoogle Scholar
15.Telkes, M.: The efficiency of thermoelectric generators. I. J. Appl. Phys. 18, 1116–1127 (1947).CrossRefGoogle Scholar
16.Telkes, M.: Solar thermoelectric generators. J. Appl. Phys. 25, 765–777 (1954).CrossRefGoogle Scholar
17.Telkes, M.: Power output of thermoelectric generators. J. Appl. Phys. 25, 1058–1059 (1954).CrossRefGoogle Scholar
18.Onsager, L.: Reciprocal relations in irreversible processes. I. Phys. Rev. 37, 405–426 (1931).CrossRefGoogle Scholar
19.Onsager, L.: Reciprocal relations in irreversible processes. II. Phys. Rev. 38, 2265–2279 (1931).CrossRefGoogle Scholar
20.Goldsmid, H.J. and Douglas, R.W.: The use of semiconductors in thermoelectric refrigeration. Br. J. Appl. Phys. 5, 386 (1954).CrossRefGoogle Scholar
21.Rowe, D.M., ed.: CRC Handbook of Thermoelectrics (RC, Boca Raton, FL, 1995).Google Scholar
22.Rowe, D.M., ed.: CRC Handbook of Thermoelectrics: Macro to Nano. (RC, Boca Raton, FL, 2006).Google Scholar
23.Riffat, S.D. and Ma, Xi.: Irreversible thermodynamics of thermoelectricity. Appl. Therm. Eng. 23, 913–935 (2003).CrossRefGoogle Scholar
24.Vining, C.B.: An inconvenient truth about thermoelectrics. Nature Mater. 8, 83–85 (2009).CrossRefGoogle ScholarPubMed
25.Shiota, I. and Miyamoto, Y., ed.: Functionally graded material 1996, in Proceedings of the 4th International Symposium on Functionally Graded Materials (Elsevier, New York, 1996).Google Scholar
26.Tritt, T.M., ed.: Recent Trends in Thermoelectric Materials Research III. Vol 71: Semiconductors and Semimetals (Academic Press, San Diego, CA, 2001).Google Scholar
27.Domenicali, C.A.: Irreversible thermodynamics of thermoelectric effects in inhomogeneous, anisotropic media. Phys. Rev. 92, 877–881 (1953).CrossRefGoogle Scholar
28.Domenicali, C.A.: Irreversible thermodynamics of thermoelectricity. Rev. Mod. Phys. 26, 237–275 (1954).CrossRefGoogle Scholar
29.Kaliazin, A.E., Kuznetsov, V.L., and Rowe, D.M.: Rigorous calculations related to functionally graded and segmented thermoelements. In Proceedings ICT 2001. Twentieth International Conference on Thermoelectrics (IEEE, 2001; pp. 286–292).Google Scholar
30.Lienhard, J.H. IV and Lienhard, J.H. V: A Heat Transfer Textbook (3rd ed.; Phlogiston Press, Cambridge, MA, 2008).Google Scholar
31.Schilz, J., Müller, E., Helmers, L., Kang, Y.S., Noda, Y., and Niino, M.: On the composition function of graded thermoelectric materials. Mater. Sci. Forum 308–311, 647–652 (1999).CrossRefGoogle Scholar
32.Egli, P.H.: Thermoelectricity (John Wiley & Sons, Inc., New York, 1960).Google Scholar
33.MacDonald, D.K.C.: Thermoelectricity: An Introduction to the Principles (Dover Publications, Inc., New York, 2006).Google Scholar
34.Ybarrondo, L.J.: Effects of surface heat transfer and spatial property dependence on the optimum performance of a thermoelectric heat pump. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, 1964).Google Scholar
35.Ybarrondo, L.J. and Sunderland, J.E.: Influence of spatially dependent properties on the performance of a thermoelectric heat pump. Adv. Energy Convers. 5, 383–405 (1965).CrossRefGoogle Scholar
36.Müller, E., Walczak, S., Seifert, W., Stiewe, C., and Karpinski, G.: Numerical performance estimation of segmented thermoelectric elements. In ICT 2005—24th International. Conference. on Thermoelectrics (Tritt, T.M., ed.; Institute of Electrical and Electronics Engineers, Inc., New York, 2005; pp. 352–357).Google Scholar
37.Seifert, W., Müller, E., and Walczak, S.: Generalized analytic description of one dimensional non-homogeneous TE cooler and generator elements based on the compatibility approach. In 25th International Conference on Thermoelectrics (Rogl, P., ed.; IEEE, Piscataway, NJ, 2006; pp. 714–719).CrossRefGoogle Scholar
38.Müller, E., Karpinski, G., Wu, L.M., Walczak, S., and Seifert, W.: Separated effect of 1d thermoelectric material gradients. In 25th International Conference on Thermoelectrics (Rogl, P., ed.; IEEE, Piscataway, NJ, 2006; pp. 201–209).Google Scholar
39.Bian, Z. and Shakouri, A.: Beating the maximum cooling limit with graded thermoelectric materials. Appl. Phys. Lett. 89, 212101 (2006).CrossRefGoogle Scholar
40.Bian, Z., Wang, H., Zhou, Q., and Shakouri, A.: Maximum cooling temperature and uniform efficiency criterion for inhomogeneous thermoelectric materials. Phys. Rev. B Condens. Matter Mater. Phys. 75, 245208 (2007).CrossRefGoogle Scholar
41.Snyder, G.J.: Thermoelectric power generation: Efficiency and compatibility. In CRC Handbook of Thermoelectrics: Macro to Nano (Rowe, D.M., ed.; Taylor & Francis, Boca Raton, FL, 2006; chap. 9).Google Scholar
42.Seifert, W., Müller, E., Snyder, G.J., and Walczak, S.: Compatibility factor for the power output of a thermogenerator. Phys. Status Solids: 1, 250–252 (2007).Google Scholar
43.Gryaznov, O.S., Moizhes, B.Ya., and Nemchinskii, V.A.: Generalized thermoelectric efficiency. Soviet Phys. Techn. Phys. 23, 975–980 (1978).Google Scholar
44.de Groot, S. and Mazur, P.: Non-Equilibrium Thermodynamics (Dover, London, 1984).Google Scholar
45.Domenicali, C.A.: Stationary temperature distribution in an electrically heated conductor. J. Appl. Phys. 25, 1310–1311 (1954).CrossRefGoogle Scholar
46.Mahan, G.D.: Density variations in thermoelectrics. J. Appl. Phys. 87, 7326–7332 (2000).CrossRefGoogle Scholar
47.Onsager, L.: Theories and problems of liquid diffusion. Annals. NY Acad. Sci. 46, 241–265 (1945).CrossRefGoogle ScholarPubMed
48.de Groot, S.R.: Thermodynamics of Irreversible Processes (North-Holland Publishing Company, Amstemdam, 1963).Google Scholar
49.Callen, H.B.: On the theory of irreversible processes. Ph.D. Thesis, MIT, Cambridge, MA, 1947.Google Scholar
50.Callen, H.B.: The application of Onsager’s reciprocal relations to thermoelectric, thermomagnetic, and galvanomagnetic effects. Phys. Rev. 73, 1349–1358 (1948).CrossRefGoogle Scholar
51.Seifert, W., Ueltzen, M., and Müller, E.: One-dimensional modelling of thermoelectric cooling. Phys. Status Solidi A 1(194), 277–290 (2002).3.0.CO;2-5>CrossRefGoogle Scholar
52.Mahan, G.D.: Inhomogeneous thermoelectrics. J. Appl. Phys. 70, 4551–4554 (1991).CrossRefGoogle Scholar
53.Harman, T.C. and Honig, J.M.: Thermoelectric and Thermomagnetic Effects and Applications (McGraw–Hill Book Company, New York, 1967).Google Scholar
54.Buist, R.J.: The extrinsic Thomson effect. In Proceedings of the 14th International Conference on Thermoelectrics, edited by Vedernikov, M.V. (A.F. Ioffe Physical-Technical Institute, St. Petersburg, Russia, 1995; pp. 301–304).Google Scholar
55.Seifert, W., Müller, E., and Walczak, S.: Local optimization strategy based on first principles of thermoelectrics. Phys. Status Solidi A 205(12), 2908–2918 (2008).CrossRefGoogle Scholar
56.Abramowitz, M. and Stegun, I.A., ed.: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th ed. (Dover Publications, Inc., New York, 1972).Google Scholar
57.Lebedev, N.N. and Silverman, R.A.: Special Functions and Their Applications (Dover Publications, Inc., New York, 1972).Google Scholar
58.Farrell, O.J. and Ross, B.: Solved Problems in Analysis: As Applied to Gamma, Beta, Legendre and Bessel Functions (Dover Publications, Inc., New York, 1971).Google Scholar
59.Bowman, F.: Introduction to Bessel Functions (Dover Publications, Inc., New York, 1958).Google Scholar
60.Mathews, G.B. and Meissel, E.: A Treatise on Bessel Functions and Their Applications to Physics (BiblioBazaar, LLC, Charleston, SC, 2008).Google Scholar
61.Ure, R. and Heikes, R.: The figure of merit of a thermoelectric generator. Adv. Energy Convers. 2, 177 (1962).CrossRefGoogle Scholar
62.Helmers, L., Müller, E., Schilz, J., and Kaysser, W.A.: Graded and stacked thermoelectric generators—Numerical description and maximisation of output power. Mater. Sci. Eng. B 56, 60–68 (1998).CrossRefGoogle Scholar
63.Ursell, T.S. and Snyder, G.J.: Compatibility of segmented thermoelectric generators. In Twenty-First International Conference on Thermoelectrics, edited by Thierry Caillat/G. Jeffrey Snyder (IEEE, 2002; pp. 412–417).Google Scholar
64.Snyder, G.J.: Application of the compatibility factor to the design of segmented and cascaded thermoelectric generators. Appl. Phys. Lett. 84, 2436–2438 (2004).CrossRefGoogle Scholar
65.Seifert, W., Zabrocki, K., Snyder, G.J., and Müller, E.: Power-related compatibility and maximum electrical power output of a thermogenerator. Phys. Status. Solidi A 207, 2399–2406 (2010).CrossRefGoogle Scholar
66.Moizhes, B.Ya: The influence of the temperature dependence of physical parameters on the efficiency of thermoelectric generators and refrigerators. Sov. Phys. Solid State 2, 728–737 (1960).Google Scholar
67.Borrego, J.M.: Carrier concentration optimization in semiconductor thermoelements. IEEE Trans. Electron Devices 10, 364–370 (1963).CrossRefGoogle Scholar
68.Borrego, J.M.: Approximate analysis of the operation of thermoelectric generators with temperature dependent parameters. IEEE Trans. Aerospace 2, 4–9 (1964).CrossRefGoogle Scholar
69.Efremov, A.A. and Pushkars, A.S.: Energy calculation of thermoelements with arbitrary temperature dependence of thermoelectric properties of materials by heat balance technique. Energy Convers. 11, 101–104 (1971).CrossRefGoogle Scholar
70.Muto, A., Kraemer, D., Hao, Q., Ren, Z.F., and Chen, G.: Thermoelectric properties and efficiency measurements under large temperature differences. Rev. Sci. Instrum. 80, 093901 (2009).CrossRefGoogle ScholarPubMed
71.Zabrocki, K., Müller, E., and Seifert, W.: One-dimensional modeling of thermogenerator elements with linear material profiles. J. Electron. Mater. 39, 1724–1729 (2010).CrossRefGoogle Scholar
72.Kuznetsov, V.L., Kuznetsova, L.A., Kaliazin, A.E., and Rowe, D.M.: High performance functionally graded and segmented Bi2Te3-based materials for thermoelectric power generation. J. Mater. Sci. 37, 2893–2897 (2002).CrossRefGoogle Scholar
73.Kuznetsov, V.L. and Edwards, P.P.: Functional materials for sustainable energy technologies: Four case studies. ChemSus Chem 3, 44–58 (2010).CrossRefGoogle ScholarPubMed
74.Dashevsky, Z., Shusterman, S., Dariel, M.P., and Drabkin, I.: Thermoelectric efficiency in graded indium-doped PbTe crystals. J. Appl. Phys. 92, 1425–1430 (2002).CrossRefGoogle Scholar
75.Dashevsky, Z., Gelbstein, Y., Edry, I., Drabkin, I., and Dariel, M.P.: Optimization of thermoelectric efficiency in graded materials. In Proceedings of the 22nd International Conference on Thermoelectrics, edited by Scherrer, H. and Tedenac, J.-C. (IEEE, 2003; pp. 421–424).Google Scholar
76.Gelbstein, Y., Dashevsky, Z., and Dariel, M.P.. High performance n-type PbTe-based materials for thermoelectric applications. Phys. B Condens. Matter 363(1–4), 196–205 (2005).CrossRefGoogle Scholar
77.Müller, E., Drašar, Č., Schilz, J., and Kaysser, W.A.: Functionally graded materials for sensor and energy applications. Mater. Sci. Eng. A 362, 17–39 (2003).CrossRefGoogle Scholar
78.Ziolkowski, P., Karpinski, G., Platzek, D., Stiewe, C., and Müller, E.: Application overview of the potential Seebeck microscope. In 25th International Conference of Thermoelectrics 06 (Rogl, P., ed.; 2006; pp. 684–688).CrossRefGoogle Scholar
79.Platzek, D., Karpinski, G., Drasar, C., and Müller, E.: Seebeck scanning microprobe for thermoelectric FGM. Mater. Sci. Forum 492–493, 587–592 (2005).CrossRefGoogle Scholar
80.Sherman, B., Heikes, R.R., and Ure, R.W. Jr.: Calculation of efficiency of thermoelectric devices. J. Appl. Phys. 31, 1–16 (1960).CrossRefGoogle Scholar
81.Sherman, B., Heikes, R.R., and Ure, R.W. Jr.: Calculation of efficiency of thermoelectric devices. In Thermoelectric Materials and Devices (Materials Technology Series, Cadoff, I.B. and Miller, E., ed.; Reinhold Publishing Cooperation, New York, 1960; pp. 199–226).Google Scholar
82.Anatychuk, L.I., Luste, O.J., and Vikhor:, L.N. Optimal functions as an effective method for thermoelectric devices design. In Fifteenth International Conference on Thermoelectrics, edited by Fleurial, J.-P. (IEEE, 1996; pp. 223–226).CrossRefGoogle Scholar
83.Anatychuk, L.I. and Vikhor, L.N.: Functionally graded materials and new prospects for thermoelectricity use. In Proceedings ICT ’97. Sixteenth International Conference on Thermoelectrics, edited by Heinrich, ArminSchumann, Joachim (IEEE, 1997; pp. 588–591).Google Scholar
84.Hogan, T.P. and Shih, T.: Modeling and characterization of power generation modules based on bulk materials. In CRC Handbook of Thermoelectrics: Macro to Nano (Rowe, D.M., ed.; Taylor & Francis, Boca Raton, FL, 2006; chap. 12).Google Scholar
85.Norwood, M.H.: A comparison of theory and experiment for a thermoelectric cooler. J. Appl. Phys. 32, 2559–2563 (1961).CrossRefGoogle Scholar
86.Power, M. and Handelsman, R.A.: Generalized calculation of thermoelectric efficiency. Adv. Energy Convers. 1, 45–60 (1961).CrossRefGoogle Scholar
87.Chen, M., Rosendahl, L.A., Condra, T.J., and Pedersen, J.K.: Numerical modeling of thermoelectric generators with varying material properties in a circuit simulator. IEEE Trans. Energy Convers. 24, 112–124 (2009).CrossRefGoogle Scholar
88.Rowe, D.M. and Min, G.: Evaluation of thermoelectric modules for power generation. J. Power Sources 73, 193–198 (1998).CrossRefGoogle Scholar
89.Jacquot, A., Jägle, M., König, J., Ebling, D.G., and Böttner, H.: Theoretical study of the Harman method for evaluating the thermoelectric performance of materials and components at high temperature. In Proceedings of the 5th European Conference on Thermoelectrics (2007).Google Scholar
90.Jägle, M.: Simulating thermoelectric effects with finite element analysis using COMSOL. In Proceedings of the 5th European Conference on Thermoelectrics (2007).Google Scholar
91.López, A., Villasevil, F., Noriega, G., and Platzek, D.: Thermoelectric integrated numerical modeling process of a temperature and humidity control device apply to vehicles for fogging preventing. In Proceedings of the 5th European Conference on Thermoelectrics (2007).Google Scholar
92.Freunek, M., Müller, M., Ungan, T., Walker, W., and Reindl, L.M.: New physical model for thermoelectric generators. J. Electro. Mater. 38, 1214–1220 (2009).CrossRefGoogle Scholar
93.Fraisse, G., Lazard, M., Goupil, C., and Serrat, J.Y.: Study of a thermoelement’s behaviour through a modelling based on electrical analogy. Int. J. Heat and Mass Transfer 53, 3503–3512 (2010).CrossRefGoogle Scholar
94.Morega, A.M., Morega, M., and Panait, M.A.: Structural optimization of a thermoelectric generator by numerical simulation. Rev. Roum. Sci. Tech. Serie Électrotech. Énergétique 55, 3–12 (2010).Google Scholar
95.Sandoz-Rosado, E. and Stevens, R.: Robust finite element model for the design of thermoelectric modules. J. Electron. Mater. 39, 1848–1855 (2010).CrossRefGoogle Scholar
96.Ebling, D., Bartholomé, K., Bartel, M., and Jägle, M.: Module geometry and contact resistance of thermoelectric generators analyzed by multiphysics simulation. J. Electron. Mater. 39, 1376–1380 (2010).CrossRefGoogle Scholar
97.Weisstein, E.W.: Bessel function. From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/Bessetfunction.html/Google Scholar
98.Weisstein, E.W.: Sine integral. From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/SineIntegral.htmlGoogle Scholar
99.Weisstein, E.W.: Cosine integral. From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/CosineIntegral.htmlGoogle Scholar
100.Weisstein, E.W.: Dilogarithm. From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/Dialogarithm.html.Google Scholar
101.Watson, G.N.: A Treatise on the Theory of Bessel Functions (Cambridge University Press, London, 1922).Google Scholar