Article contents
Numerical analysis of different methods to calculate residual stresses in thin films based on instrumented indentation data
Published online by Cambridge University Press: 01 June 2012
Abstract
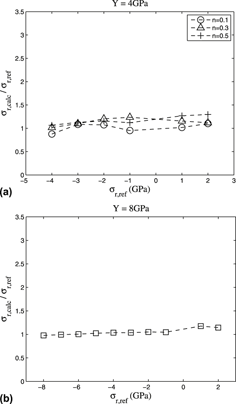
In this work, different methods to estimate the value of thin film residual stresses using instrumented indentation data were analyzed. This study considered procedures proposed in the literature, as well as a modification on one of these methods and a new approach based on the effect of residual stress on the value of hardness calculated via the Oliver and Pharr method. The analysis of these methods was centered on an axisymmetric two-dimensional finite element model, which was developed to simulate instrumented indentation testing of thin ceramic films deposited onto hard steel substrates. Simulations were conducted varying the level of film residual stress, film strain hardening exponent, film yield strength, and film Poisson’s ratio. Different ratios of maximum penetration depth hmax over film thickness t were also considered, including h/t = 0.04, for which the contribution of the substrate in the mechanical response of the system is not significant. Residual stresses were then calculated following the procedures mentioned above and compared with the values used as input in the numerical simulations. In general, results indicate the difference that each method provides with respect to the input values depends on the conditions studied. The method by Suresh and Giannakopoulos consistently overestimated the values when stresses were compressive. The method provided by Wang et al. has shown less dependence on h/t than the others.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2012
References
REFERENCES
- 10
- Cited by

