Article contents
In situ measurement of bulk modulus and yield response of glassy thin films via confined layer compression
Published online by Cambridge University Press: 02 March 2020
Abstract
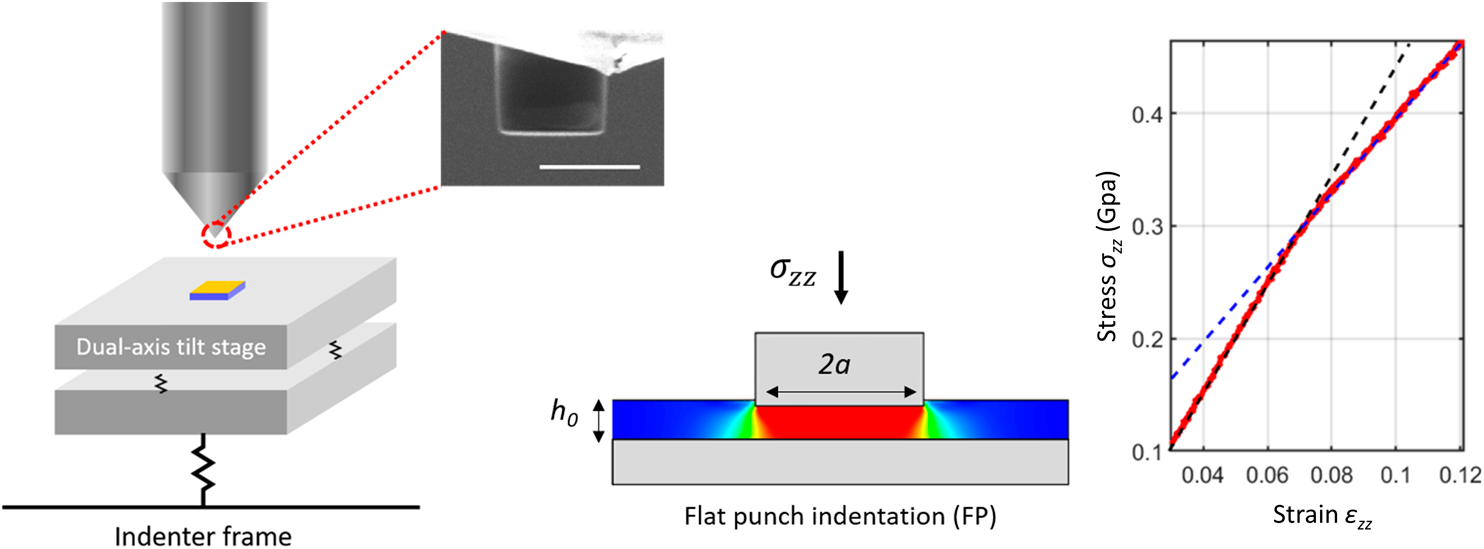
The measurement of thin film mechanical properties free from substrate influence remains one of the outstanding challenges in nanomechanics. Here, a technique based on indentation of a supported film with a flat punch whose diameter is many times the initial film thickness is introduced. This geometry generates a state of confined uniaxial strain for material beneath the punch, allowing direct access to intrinsic stress versus strain response. For simple elastic–plastic materials, this enables material parameters such as elastic modulus, bulk modulus, Poisson's ratio, and yield stress to be simultaneously determined from a single loading curve. The phenomenon of confined plastic yield has not been previously observed in thin films or homogeneous materials, which we demonstrate here for 170 -470 nm thick polystyrene (PS), polymethyl-methacrylate (PMMA) and amorphous Selenium films on silicon. As well as performing full elastic -plastic parameter extraction for these materials at room temperature, we used the technique to study the variation of yield stress in PS to temperatures above the nominal glass transition of 100 °C.
Information
- Type
- Article
- Information
- Copyright
- Copyright © Materials Research Society 2020
Footnotes
Present address: Metallurgical Engineering and Materials Science, Indian Institute of Technology Bombay, Mumbai 400076, India.
This article has been corrected since its original publication. An erratum notice detailing these changes was also published (doi: 10.1557/jmr.2020.67)
References
A correction has been issued for this article:
- 8
- Cited by
Linked content
Please note a has been issued for this article.

