Article contents
A first-principles study on hot crack mechanism in Mg-Al-Ca alloys
Published online by Cambridge University Press: 20 March 2012
Abstract
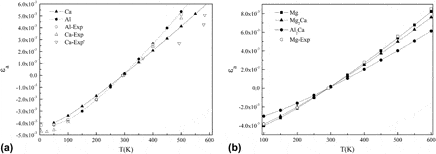
The use of Mg-Al-Ca alloys is limited mainly due to the hot crack defect. The exact mechanism of hot crack formation is not yet clearly understood. In this article, the hot crack mechanism is established from the present first-principles calculations based on the density functional theory and density functional perturbation theory . The thermal expansion behavior of Mg and the critical compounds Mg2Ca and Al2Ca in Mg-Al-Ca alloys is calculated. According to the present calculations, Mg2Ca is almost equal to Mg in thermal expansion, whereas the same in Al2Ca is much too lower. Al2Ca improves the creep resistance of Mg-Al-Ca alloys due to its high thermal stability, but it also accounts for the hot crack defect due to very small thermal expansion.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2012
References
REFERENCES
- 6
- Cited by

