Article contents
Effect of the ∑5(310)/[001]θ = 53.1° grain boundary on the incipient yield of bicrystal copper: A quasicontinuum simulation and nanoindentation experiment
Published online by Cambridge University Press: 21 February 2013
Abstract
To study the initial plasticity during the nanoindentation of face-centered cubic bicrystal materials at the micro- and nanoscales, a 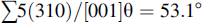 $\sum {5(310)/[001]} {\rm{\theta }} = 53.1\circ $ symmetrical tilt grain boundary (GB) model of bicrystal copper was constructed using the quasicontinuum method. The nanoindentation process of the model was then simulated, and a group of indents across the GB during a bicrystal copper nanoindentation experiment were performed. The effect of the GB on the incipient yield was studied when the transition from elastic to plastic deformation and the first dislocation emission occur. The results show that the maximum incipient load appears in the center of the boundary; the load first increases and then gradually decreases until it presents no further significant changes when the indenter is far from the GB. It is observed that theoretical simulation results are in good agreement with those of the experimental measurement. The incipient yield force was affected by the size and the position of the indenter, the structure of the boundary, and the first dislocation emission.
$\sum {5(310)/[001]} {\rm{\theta }} = 53.1\circ $ symmetrical tilt grain boundary (GB) model of bicrystal copper was constructed using the quasicontinuum method. The nanoindentation process of the model was then simulated, and a group of indents across the GB during a bicrystal copper nanoindentation experiment were performed. The effect of the GB on the incipient yield was studied when the transition from elastic to plastic deformation and the first dislocation emission occur. The results show that the maximum incipient load appears in the center of the boundary; the load first increases and then gradually decreases until it presents no further significant changes when the indenter is far from the GB. It is observed that theoretical simulation results are in good agreement with those of the experimental measurement. The incipient yield force was affected by the size and the position of the indenter, the structure of the boundary, and the first dislocation emission.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2013
References
REFERENCES
- 7
- Cited by

