Introduction
With the dramatic achievements and significant progresses in the last decade, Integrated Computational Materials Engineering (ICME) provides an unparalleled designing and manufacturing paradigm in accelerating the R&D of advanced materials [Reference Pollock, Allison, Backman, Boyce, Gersh, Holm, Lesar, Long, IV, Schirra, Whitis and Woodward1, Reference Wang, Li, Liu and Liu2, Reference Liu, Chen, Raghavan, Du, Sofo, Langer and Wolverton3, Reference Liu4, Reference Frankel, Hatcher, Snyder, Sebastian, Olson, Vernon, Everhart and Carroll5]. It is recognized that recent advances in superpower computation [6], additive manufacturing [Reference Pollock7, Reference Garcia, Jones, Zhu and Yu8], big data [Reference Jose and Ramakrishna9], data mining [Reference de Pablo, Jackson, Webb, Chen, Moore, Morgan, Jacobs, Pollock, Schlom, Toberer, Analytis, Dabo, DeLongchamp, Fiete, Grason, Hautier, Mo, Rajan, Reed, Stevanovic, Suntivich, Thornton and Zhao10], machine learning [Reference de Pablo, Jackson, Webb, Chen, Moore, Morgan, Jacobs, Pollock, Schlom, Toberer, Analytis, Dabo, DeLongchamp, Fiete, Grason, Hautier, Mo, Rajan, Reed, Stevanovic, Suntivich, Thornton and Zhao10, Reference Tanaka, Rajan and Wolverton11, Reference Liu, Zhao, Ju and Shi12], cloud computation [13], metallic materials ontology [Reference Zhang, Pan, Zhao and Li14], graphic knowledge [Reference Zhang, Liu, Li and Pan15, Reference Picklum and Beetz16], and so on, provide an opportunity to create a designing and manufacturing paradigm shift. For instance, the high-throughput-type and the combinatorial approaches integrating both the bottom-up designing and the top-down engineering set up the digital twin feature of composition–processing–structure–property–performance (CPSPP) workflow process at multiscales [Reference Meredig and Wolverton17, Reference Olson18, Reference Xiong and Olson19, Reference Chen, Shin and Saal20, Reference Zhao21, Reference Zhao22, Reference Bedewy23], which is known as the data-driven ICME [Reference Wang, Li, Liu and Liu2]. The advanced structural metal materials are developed/manufactured crossing multiscales, from Electronics to Phases [Reference Zhou, Wang, Liu, Arroyave and Horstemeyer24, Reference Huang, Grabowski, Zhang, Lai, Tasan, Sandlöbes, Raabe and Neugebauer25], i.e., from Atom to Autos [Reference Krajewski, Hector, Qi, Mishra, Sachdev, Bower and Curtin26], from CALPHAD to Flight [Reference Olson and Kuehmann27]. Moreover, to lead the world in scientific and technological innovations, global competitors have launched various strategies/programs and boosted the development of new manufacturing technologies, which include the Materials Genome Initiative (MGI) [28] and the Advanced Manufacturing of United States [29], the China's Materials Genome Engineering (MGE) & Made in China 2025 [Reference Zhou, Li, Zhou, Wang, Zang and Meng30], the European Union's Industry 4.0 Programme [Reference Zhong, Xu, Klotz and Newman31], the Industry 2050 of United Kingdom [32], the Intelligence Manufacturing System 2020 (IMS2020) & Toward Technology Innovation of Society 5.0 of Japan, the Industry Innovation 3.0 of Korea, and so on [Reference Wang, Li, Liu and Liu2]. In fact, more than four decades ago, the combinational approaches involving high-throughput synthesis and characterization of multiple-alloy compositions have been utilized in materials sciences, to rapidly determine phase diagrams in multicomponent spaces and screened physical and mechanical properties [Reference George, Raabe and Ritchie33, Reference Xiang, Sun, Briceño, Lou, Wang, Chang, Wallace-Freedman, Chen and Schultz34].
Recently, we discussed the frameworks of data-driven ICME in the last two years, presenting key aspects of principles, benchmarks, standards, databases, platforms, and toolkits via various case studies [Reference Wang, Li, Liu and Liu2]. A universal format of Data Identifier (DID) code consisting of a set of Build Chains is proposed [Reference Wang, Li, Lin, Tang, Wang, Guan, Ye, Dai, Gao, Kou, Song, Zhou, Ma, Liu, Li and Liu35], which is in line with the classical form of identifier utilized in both international and national standards and can serve the Inheritable Integrated Intelligent Manufacturing (I3M). It is worth mentioning that the inheritable feature indicates the original concept of “Materials Genome” in the materials discovery/design/manufacturing. In this article, a brief review of our case studies of data-driven ICME for intelligently discovering advanced structural metal materials is presented, which include the light-weight materials (Ti, Mg, and Al alloys), refractory high-entropy alloys (RHEAs), and superalloys for high temperature applications. The basic bonding in terms of topology and electronic structures is recommended to be considered as the building blocks/units constructing the microstructures of advanced materials, known as the so-called Materials Genome. It is highlighted that the bonding charge density could not only provide an atomic and electronic insight into the physical nature of chemical bond of materials but also reveal the fundamental strengthening/embrittlement mechanism and the local phase transformations of planar defects, paving a path in accelerating the development of advanced metal materials via interfacial engineering approach. Perspectives on the knowledge-based modeling/simulations, machine-learning knowledge base, platform, and next-generation workforce for sustainable ecosystem of ICME are highlighted, thus to call for more duty on the developments of advanced structural metal materials and enhancement of research productivity and collaboration.
Methodologies
Digital twin design paradigm at ICME era
Toward the novel design paradigm in ICME era, the CPSPP relationship/workflow process displays a digital twin feature, indicating that there is digital world designing/manufacturing the advanced materials, as shown in Fig. 1. Each experimental process in terms of top-down design can be matched in the theoretical one defined as the bottom-up design, which basically presents the foundation of combinatorial approach integrating the advanced technologies, such as high-throughput computations, data mining, machine learning, intelligent/additive manufacturing, cloud computation, and internet of things [Reference Zhong, Xu, Klotz and Newman31, Reference Liu, Furrer, Kosters and Holmes36, Reference Aspuru-Guzik, Persson and Tribukait-Vasconelos37]. Moreover, referring to those three aspects of MGI infrastructures, a Human–Cyber–Physics system (HCP) has been proposed and emphasized in the frames of MGE and Made in China 2025 [Reference Zhou, Li, Zhou, Wang, Zang and Meng30], which is as same as the Cyber–Physical–Social ecosystem reported to U.S. NASA Scientific and Technical Information Program. Both of them will play a key role in accelerating the model-based/knowledge-based concurrent design, development, and deployment of materials and systems throughout the product life cycles [Reference Wang, Li, Liu and Liu2, Reference Wang, Li, Lin, Tang, Wang, Guan, Ye, Dai, Gao, Kou, Song, Zhou, Ma, Liu, Li and Liu35, Reference Liu, Furrer, Kosters and Holmes36]. While the interaction of Human–Cyber indicates the importance of knowledge-based computations/design, the interactions of Human–Physics and Cyber–Physics highlight key roles of the high-throughput manufacturing/experimental validations and the artificial intelligence/machine learning in the HCPs. It is expected that digital design and intelligent manufacturing could be improved dramatically through the digital twin design paradigm.
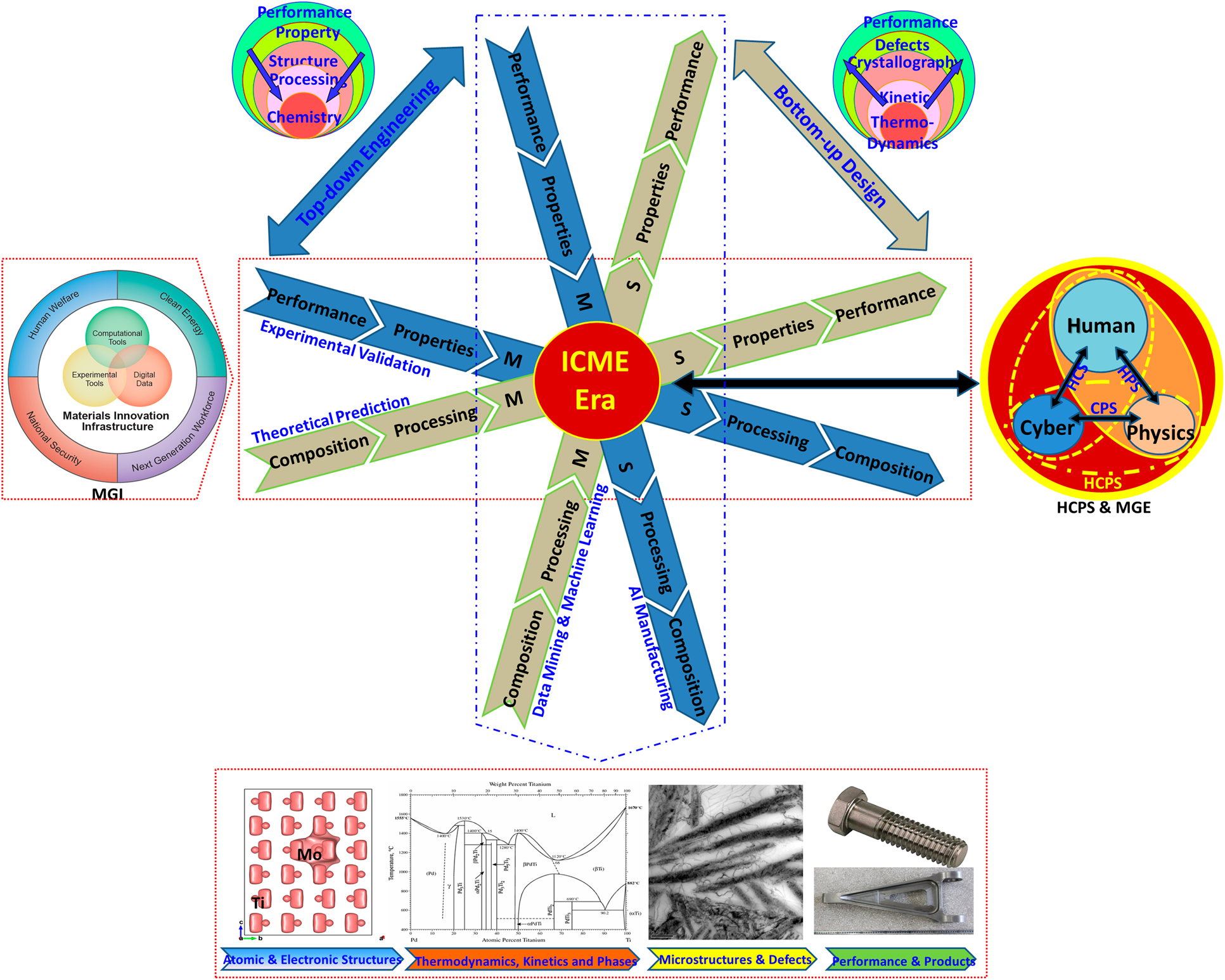
Figure 1: Atom-to-Product processing chain of Ti alloys in line with the digital-twin design paradigm in ICME Era [Reference Wang, Li, Liu and Liu2].
Furthermore, shown as the Atom-to-Product processing chain of Ti alloys in Fig. 1, it can be seen that integrated various theoretical and experimental approaches at multiscales will be essential to fabricate a high-quality product with a novel composition and reduced designing time and cost. Actually, the letter “I” in ICME highlights a crucial element needed for implementing the predictive models and simulations into materials design and development across the product–development cycle, in which the bottlenecks are related to the need for the development of new fundamental theoretical methodologies and frameworks for linking atomistics, microstructure, processing, and property models across length and time scales [38]. Modeling/simulation for composition optimization/design, structure analysis/characterization, physics-based performance (structures), and manufacturing can be accelerated by the multiscale calculations, including density functional theory (DFT) calculations, ab initio molecular dynamics (AIMD), classical MD simulations, CALculated PHAse Diagram (CALPHAD) modeling, phase-field simulations, and (kinetic) Monte Carlo simulations.
In fact, based on the density functional theory, high-throughput first-principles calculations can not only provide the thermodynamic properties combined with CALPHAD but also support kinetic properties, mechanical properties, and other fundamental physical properties, as shown in Fig. 2. Those properties also indicate their further contributions in the multiscale modeling or computations together with the corresponding crossover experimental validations. It is worth mentioning that various kinds of databases have boosted with the significant enhancement of computational power and investigations of research efforts/supports, which is one third of the key Materials Genome infrastructures. The multiscale computational materials science, open source cyber infrastructure for data management, and an integrated approach combining computation and experiments to accelerate the development of advance materials have become three significant research fields [Reference Liu41, Reference Chen42]. Together with the foundations and milestones of MGI/MGE and ICME, the recent progresses emphasizing on the importance of computational materials/platform/system for the future have been released [Reference Zhou, Wang, Liu, Arroyave and Horstemeyer24, Reference Liu, Furrer, Kosters and Holmes36, Reference Shin and Saal39, 40, Reference Robertson, Schuh, Vetrano, Browning, Field, Jensen, Miller, Baker, Dunand, Dunin-Borkowski, Kabius, Kelly, Lozano-Perez, Misra, Rohrer, Rollett, Taheri, Thompson, Uchic, Wang and Was43]. Materials Genome has been recommended as a set of databases (information) for predicting materials properties of virtual alloy compositions and its response to processing and usage conditions [Reference Kaufman and Agren44]. Moreover, data—the basic unit building block of database and advanced computational algorithms such as machine learning, data mining, deep learning, and artificial intelligence—have been recognized as the third essential digital resource in the I3M beside the natural mineral materials and the financial funds. The flow chain of “Data-Cyber-Knowledge-Wisdom” presents the inheritable feature of the data in the frameworks of “Materials Genome,” which is also highlighted in the Data-driven ICME designing paradigm of advanced materials.
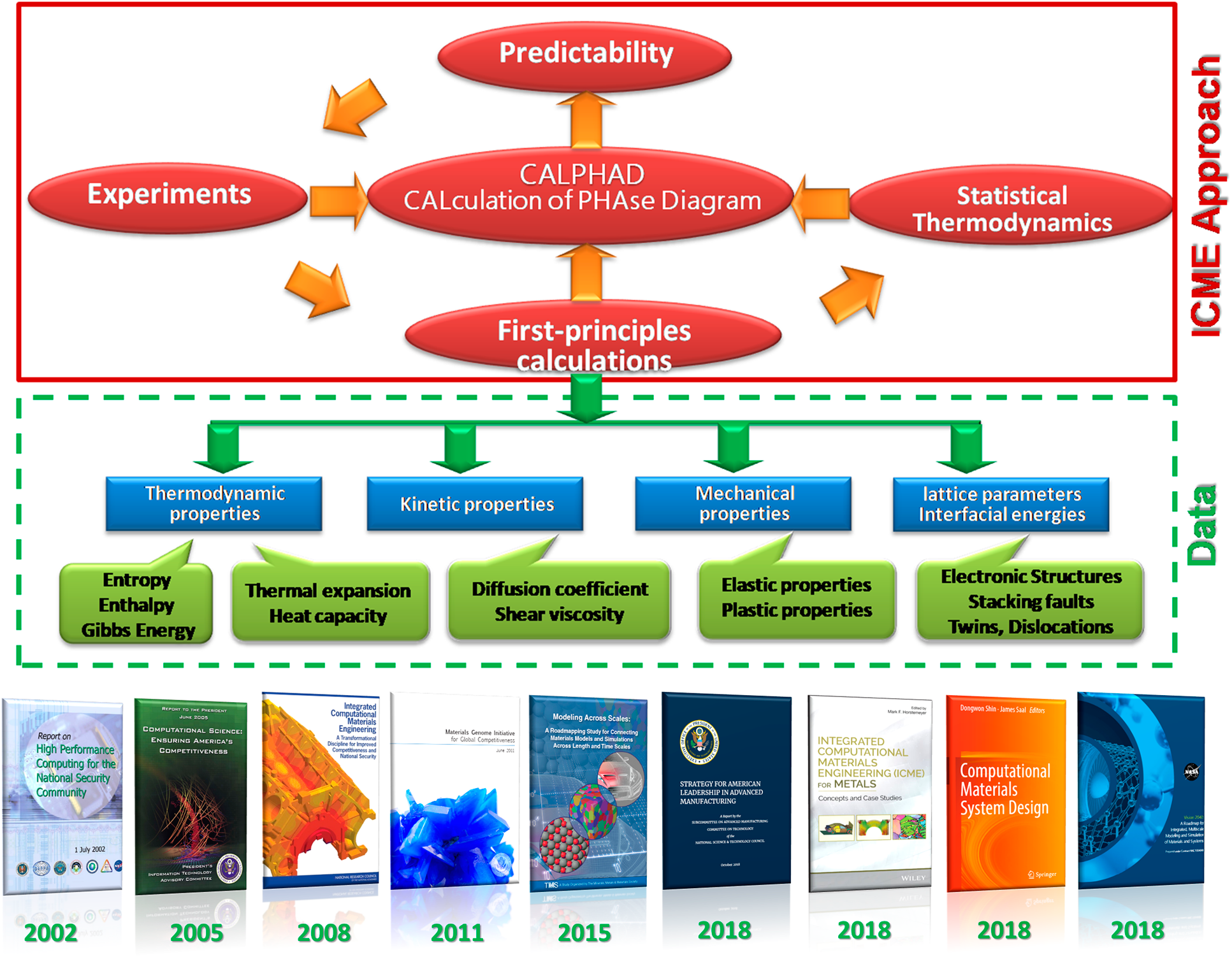
Figure 2: The proposed data-driven ICME approach [Reference Wang, Li, Liu and Liu2, Reference Zhou, Wang, Liu, Arroyave and Horstemeyer24] together with the corresponding foundations and milestones [Reference Zhou, Wang, Liu, Arroyave and Horstemeyer24, Reference Liu, Furrer, Kosters and Holmes36, Reference Shin and Saal39, 40].
Electrons to phases and properties: key roles of microstates
Since the structure dominates the properties and performance in the CPSPP workflow process, the structure predictions and characterization play a key role in accelerating the discovery of advanced materials in a cost-effective approach. Predicting crystal structures with data mining of quantum calculations (i.e., high-throughput electronic structure calculations together with structural data mining algorithm or phenomenological models) allows the identification of new materials [Reference Curtarolo, Morgan, Persson, Rodgers and Ceder45, Reference Eriksson46, Reference Taylor, Lu, Saal, Frankel and Scully47, Reference Saal, Kirklin, Aykol, Meredig and Wolverton48]. It should be highlighted that the atomic and electronic basis for the fundamental strengthening mechanisms and the physical nature of chemical bonds can be revealed comprehensively by bonding charge density [Reference Wang, Li, Liu and Liu2]. On the one hand, the hidden topological orders or short-range orders (SRO) or clusters or microstates should be considered when constructing the structures of multicomponent alloys theoretically and experimentally. The microstates/configurations/local orders are essential to reveal their structure–property relationship [Reference Wang, Wang, Lin, Zou, Wu, Hu, Shang, Darling, Wang, Hui, Li, Kecskes, Liaw and Liu49, Reference Wu, Li, Wang and Liu50, Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51, Reference Lei, Liu, Wu, Wang, Jiang, Wang, Hui, Wu, Gault, Kontis, Raabe, Gu, Zhang, Chen, Wang, Liu, An, Zeng, Nieh and Lu52]. Predictive models have been proposed to reveal the hydrogen trapping and bubbling in nanovoids in body-centered-cubic (BCC) metals, which integrate the multiscale calculations including DFT calculations, classical MD simulations, and kinetic Monte Carlo simulations [Reference Hou, Kong, Wu, Song and Liu53]. The microstates/clusters dominated shear bands or serrations of high-entropy alloys and metallic glasses during deformation are reported [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51, Reference Greer, Cheng and Ma54]. On the other hand, “defects at the atomic scale, which are revealed in the electronic structure, affect the macroscopic mechanical properties such as the elastic and plastic deformation,” which is highlighted in the review of Four Decades of Materials Developments Transform Society reported by Philip Ball [Reference Ball55]. It is recommended that correlations between structural defects and local phase transformations should be considered [Reference Wang, Shang, Wang, Darling, Kecskes, Mathaudhu, Hui and Liu56, Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Krasheninnikov58, Reference Kosterlitz59], especially when designing novel advanced materials via the Grain-boundary Engineering or Interface Engineering approach. For instance, in the view of bonding charge density, the local phase transformation of several kinds of planar faults has been captured/reported, such as the connections between stacking faults (growth fault—I1, deformation fault—I2, and extrinsic fault—EF) and long periodic stacking ordered structures/phases (LPSOs) of Mg alloys [Reference Wang, Shang, Wang, Darling, Kecskes, Mathaudhu, Hui and Liu56], the local FCC-HCP transformation in the grain boundary of Fe and Al alloys [Reference Wang, Shang, Wang, Hu, Darling, Kecskes, Mathaudhu, Hui and Liu60, Reference Wang, Zou, Lin, Tang, Zhang, Sun, Guan, Tang, Wang, Kou, Gao, Song, Ma and Li61], the local D023 and D022 phase transformations in superlattice intrinsic stacking fault (SISF), and antiphase boundaries (APBs) of superalloys [Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Zhang, Li, Wang, Li, Tang, Wang, Kou, Shang, Wang, Kecskes, Hui, Feng and Liu62].
Moreover, with the guidance of the electron redistributions in terms of bonding charge density [Reference Wang, Shang, Wang, Darling, Kecskes, Mathaudhu, Hui and Liu56, Reference Wang, Wang, Chen and Liu65, Reference Nakashima, Smith, Etheridge and Muddle66, Reference Wang, Wang, Shang, Darling, Kim, Tang, Kou, Mathaudhu, Hui, Li, Kecskes and Liu67] and electron localization functions [Reference Silvi and Savin68, Reference Wang, Shang, Wang, Darling, Mathaudhu, Hui and Liu69], new insights are provided into those microstates/SROs/clusters and structural phase transformations quantitatively and qualitatively. They are utilized to reveal the physical nature of chemical bond of pure metals (Al [Reference Wang, Zou, Lin, Tang, Zhang, Sun, Guan, Tang, Wang, Kou, Gao, Song, Ma and Li61, Reference Wang, Darling, Wang, Shang, Kecskes, Hui and Liu70], Ag [Reference Wang, Kang, Wang, Ding, Zhou and Yang71], Fe [Reference Wang, Shang, Wang, Hu, Darling, Kecskes, Mathaudhu, Hui and Liu60, Reference Hu, Wang, Wang, Darling, Kecskes and Liu72], Mg, Ti [Reference Wang, Zhang, Li, Zou, Tang, Wang, Lin, Wang, Kou and Xu73, Reference Zou, Li, Wang, Zhang, Tang, Wang, Lin, Wang, Kou and Xu74]), alloys (Co-based [Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Zhang, Li, Wang, Li, Tang, Wang, Kou, Shang, Wang, Kecskes, Hui, Feng and Liu62] and Ni-based [Reference Manga, Shang, Wang, Wang, Liang, Crespi and Liu75]alloys), Fe-X alloys [Reference Wang, Shang, Wang, Hu, Darling, Kecskes, Mathaudhu, Hui and Liu60, Reference Hu, Wang, Wang, Darling, Kecskes and Liu72], Mg-RE-TM alloys [Reference Wang, Wang, Shang, Darling, Kim, Tang, Kou, Mathaudhu, Hui, Li, Kecskes and Liu67, Reference Kim, Wang, Shang, Kecskes, Darling and Liu76], RHEAs [Reference Wang, Wang, Lin, Zou, Wu, Hu, Shang, Darling, Wang, Hui, Li, Kecskes, Liaw and Liu49, Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51], Ti-X alloys [Reference Wang, Zhang, Li, Zou, Tang, Wang, Lin, Wang, Kou and Xu73, Reference Zou, Li, Wang, Zhang, Tang, Wang, Lin, Wang, Kou and Xu74]), metal melts (vit1 metallic glass [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51], Al–Cu [Reference Wang, Han, Fang, Wang, Liang, Shang, Wang, Liu, Kecskes, Mathaudhu, Hui and Liu77]), oxides (AgO [Reference Wang, Kang, Wang, Ding, Zhou and Yang71], Ag2O [Reference Wang, Kang, Wang, Ding, Zhou and Yang71], Ag7O8NO3 [Reference Wang, Zhao, Zhao, Wang, Liu, Gu, Li, Zhang, Huang and Yang78], and Fe3O), semiconductors (graphene [Reference Wang, Wang, Chen and Liu65], sulfur [Reference Shang, Wang, Guan, Wang, Fang, Anderson and Liu79], sulfides [Reference Shang, Wang, Guan, Wang, Fang, Anderson and Liu79], and SiC [Reference Yang, Kiraly, Wang, Shang, Cao, Zeng, Zhao, Li, Liu, Cai and Huang80]), and structural defects (stacking faults [Reference Zhang, Li, Wang, Li, Tang, Wang, Kou, Shang, Wang, Kecskes, Hui, Feng and Liu62, Reference Wang, Zhang, Li, Zou, Tang, Wang, Lin, Wang, Kou and Xu73, Reference Shang, Shimanek, Qin, Wang, Beese and Liu81], APBs [Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Manga, Shang, Wang, Wang, Liang, Crespi and Liu75], grain boundaries [Reference Wang, Zou, Lin, Tang, Zhang, Sun, Guan, Tang, Wang, Kou, Gao, Song, Ma and Li61, Reference Hu, Wang, Wang, Darling, Kecskes and Liu72], and dislocations [Reference Hu, Zhao, Zhang, Yang, Zhang, Liu, Qian and Qi82, Reference Zhang, Beyerlein, Legut, Fu, Zhang, Shang, Liu, Germann and Zhang83]), which also reveal the fundamental solid-solution strengthening/embrittlement mechanism [Reference Wang, Zou, Lin, Tang, Zhang, Sun, Guan, Tang, Wang, Kou, Gao, Song, Ma and Li61, Reference Wang, Zhang, Li, Zou, Tang, Wang, Lin, Wang, Kou and Xu73] and the grain refinement mechanism [Reference Wang, Darling, Wang, Shang, Kecskes, Hui and Liu70, Reference Zou, Li, Wang, Zhang, Tang, Wang, Lin, Wang, Kou and Xu74].
Furthermore, beyond those aforementioned properties discussed in Fig. 2, other principles have been proposed in predicting the mechanical properties of pure metals and alloys based on the electronic properties, such as electron work function (EWF) [Reference Halas and Durakiewicz63] and valence electron concentration (VEC) [Reference Guo and Liu64], as shown in Fig. 3. It has been reported that supertoughening in B1 transition metal nitride alloys occurs through VEC tuning [Reference Sangiovanni, Hultman and Chirita84]. VEC has been considered as an essential training parameter in discovering new advanced high-entropy alloys. We believe that, aiming at the mechanical properties, predictions based on density functional theory [Reference Giustino85] via WEF would result in a more reliable result with physical foundations. For example, the power-law scaled properties including yield strength, hardness, elastic constant, and shear/bulk/Young's modulus of pure metals and alloys have been validated. Referring to the VEC, the advantage of EWF is that these elements in the same group of elemental periodic table can be distinguished. Thus, EWF will be more suitable than VEC to be considered as one kind of key principles designing new multicomponent alloys. Several cases studies are discussed in detail in the results and discussion.
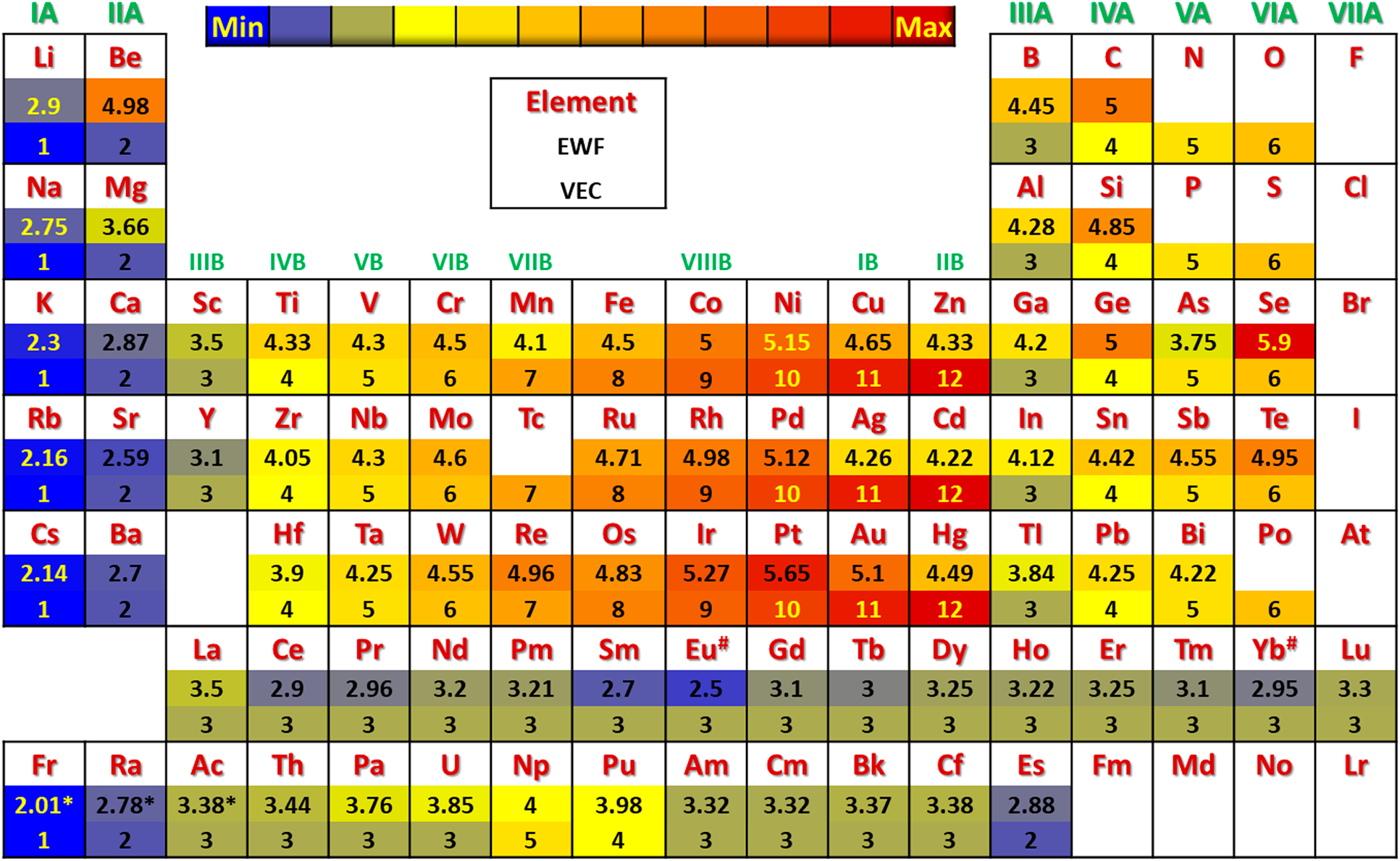
Figure 3: The periodic table of pure elements [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51] with the corresponding EWF [Reference Halas and Durakiewicz63] and VEC [Reference Guo and Liu64].
Results and discussions
Ti alloys
Because of their good strength-to-weight ratio, high melting temperature, good corrosion resistance, and excellent biocompatibility, Ti alloys are widely applied in the structural materials in aerospace, automotive, and biomedical applications [Reference Wang, Zhang, Li, Zou, Tang, Wang, Lin, Wang, Kou and Xu73, Reference Banerjee and Williams86, Reference Wen, Yamada, Shimojima, Chino, Hosokawa and Mabuchi87]. It is understood that the fundamental understanding of the effect of solute atoms on the lattice distortion and deformation behaviors of Ti alloys is critical to improve their strength and ductility in the development of advanced high-strength Ti alloys and their corresponding products. Here, we briefly present an Atom-to-Product routine via the multiscale simulations integrated with experimental validations when optimizing the properties of high-strength Ti alloys, the method of which is in line with the digital twin feature of CPSPP, shown in Figs. 3 and 4. Based on the elemental periodic table of bonding charge density (Δρ) of HCP Ti-X alloys displayed in Fig. 3(a), the coupling effects of valence electron and lattice distortion of solute atoms on the bond structures and bond morphologies are presented obviously, which reveal the atomic and electronic basis of the solid-solution strengthening mechanism of those atoms with higher value of Δρ. It is understood that a higher of value of Δρ leads to a stronger bonding.
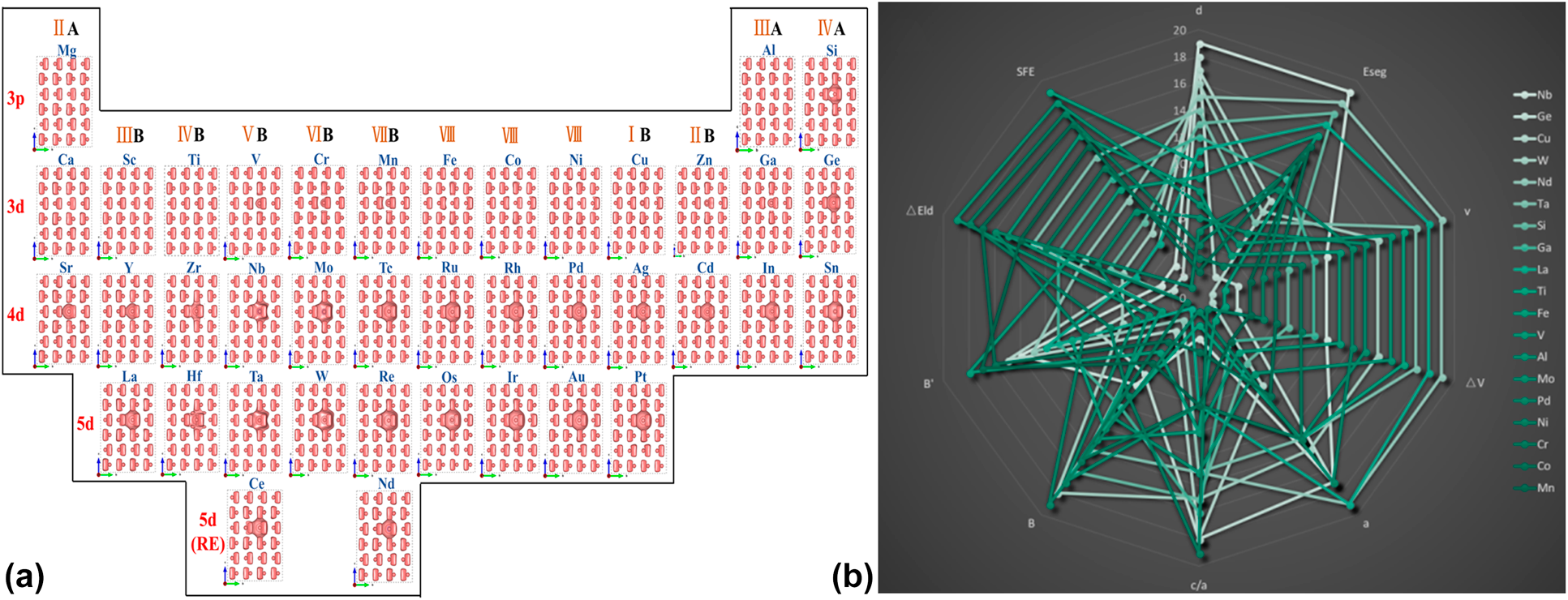
Figure 4: Databases and data mining of Ti-X alloys: (a) the elemental periodic table of bonding charge density of HCP Ti-X alloys and (b) web chart of physical properties of Ti-X alloys including lattice parameters (a and c/a), bulk modulus (B) together with it first derivative with pressure (B′), volume (V) and its variation referring to Ti (ΔV), lattice distortion energy (ΔE ld), stacking fault energy (SFE), dislocation width (d), and segregation energy to the fault layers of I2 (E seg).
With the aid of data mining or machine learning algorithm, new principles/criteria could be obtained for designing the novel Ti alloys applied in specific conditions (i.e., high load or high temperature). In particular, the fundamental properties can be predicted by high-throughput first-principles calculations shown in Fig. 3(b), which construct the foundation of data mining.
The best candidate Ti alloys with either high-strength and ductility or low steady-state creep rate can be screened out via proper criteria. In the view of web chart of physical properties of Ti-X alloys, the key parameters affecting these target properties can be distinguished, which are essential to address the model/relation. For example, the reduction of stacking fault energy (ESF) will improve the creep resistance of the materials [Reference Kassner88], which could be treated as a critical principle during designing of the high-temperature Ti alloy with good creep resistance. As for the development of ductile high-strength Ti alloys, the c/a ratio, ESF, dislocation width/density, and EWF are recommended to be considered as important criteria. The reasons are (i) the c/a ratio of HCP Ti is lower than the ideal one (1.633) and results in the most favorable slip systems consisting of the prismatic and the basal planes [Reference Salem, Kalidindi and Doherty89] since the axial ratio (i.e., c/a ratio) significantly affects the variation of twinning shear in HCP [Reference Wang, Zhang, Li, Zou, Tang, Wang, Lin, Wang, Kou and Xu73, Reference Yoo90]; (ii) the B/G ratio (1.75) has been recognized to be an identifier separating the ductile and brittle behavior [Reference Wang, Zhang, Li, Zou, Tang, Wang, Lin, Wang, Kou and Xu73, Reference Salem, Kalidindi and Doherty89]; (iii) the deformation modes of twinning and slip are closely related to the stacking faults and the mobility of the dislocation is highly pertinent to the ESF [Reference Wang, Zhang, Li, Zou, Tang, Wang, Lin, Wang, Kou and Xu73, Reference Hu and Yang91, Reference Van Swygenhoven, Derlet and Froseth92]; and (iv) a lower ESF corresponds to a large distance between dissociated partial dislocations improving strength and ductility through enhancing a higher strain-hardening coefficient, lower twinning stress, and a higher twin propensity [Reference Wang, Zhang, Li, Zou, Tang, Wang, Lin, Wang, Kou and Xu73, Reference Shang, Wang, Zhou, Wang, Darling, Kecskes, Mathaudhu and Liu93, Reference Salloom, Banerjee and Srinivasan94].
It is worth mentioning that several new designed Ti alloys are manufactured based on those aforementioned criteria, three of which are named Ti-7333A, Ti-7443, and Ti-7543, shown in Fig. 5. In fact, four main strengthening mechanisms should be considered when accurately predicting the yield strength of materials, including the solid-solution strengthening, grain refinement hardening, precipitation strengthening, and work hardening. Although only the solid-solution strengthening is considered, a strong linear correlation is addressed in Ti-7333A and Ti-7543 with the squared correlation coefficient R 2 = 0.99, shown in Fig. 5(a). On the contrary, the obvious diversity of Ti-7433 from the line in Blue–Green–Red (BGR) gradient colors is attributed to the great amount of precipitations and grain refinement effect, which is also highlighted by the blue ellipse. Due to the absence of grain size information of the reported data listed in Fig. 5(a), it is hard to derive a proper model/relation to reveal those strengthening mechanisms and the squared correlation coefficient R 2 is as low as 0.88, presenting a large diversity. On the contrary, the coupling effect of solid-solution strengthening and grain refinement hardening of our designed Ti alloys are displayed in Fig. 5(b). The corresponding relation yields a good result, matching well with the experimental one. The large diversity of Ti-7543 is attributed to the great amount of precipitations. Therefore, it can be seen that the processing parameters to control grain size and screen composition are obtained to get the target yield strength of designed Ti alloys.
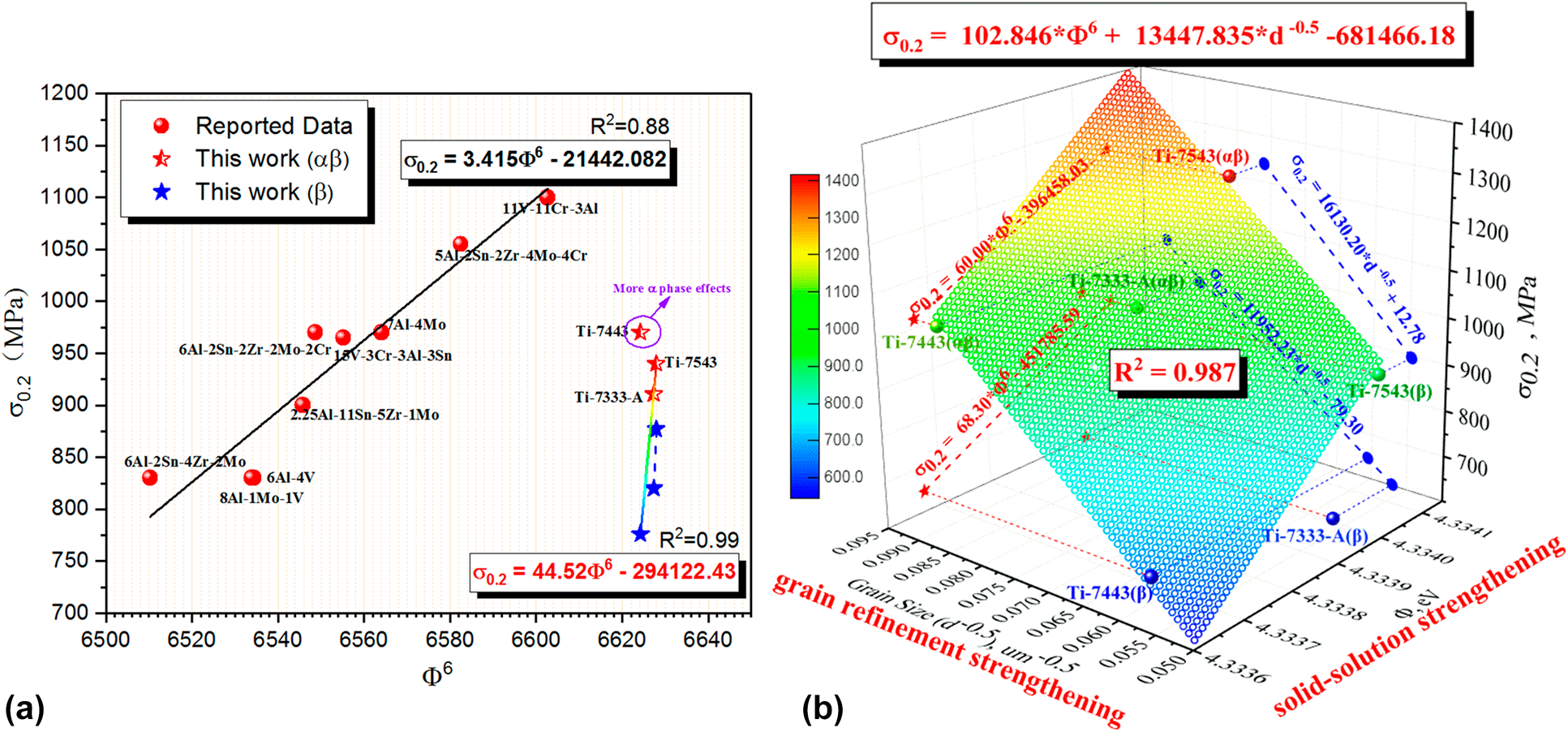
Figure 5: The predicted yield strength (σ0.2) of designed Ti alloys referring to relative Ti alloys: (a) power-law scaled σ0.2 in terms of EWF (Ф) and (b) the coupling effect of solid-solution strengthening and grain refinement hardening of our designed Ti alloys.
Figure 6 presents the digital-twin designing and manufacturing approaches for the new high-strength near β Ti7333 landing gear torque arm, systematically exploring the microstructure evolution rules, establishing the constitutive models and microstructure models of hot deformation, and addressing the prediction of phase volume fraction, average grain size, dislocation density, and macro-physical fields during hot deformation. During the die forging of titanium alloy, the stress, strain, and temperature of different parts are different, which leads to the difference in microstructure of various parts. Since the microstructures of the alloy will dominate the performance in their service life, it is important to understand the microstructure evolution of titanium alloy under different process conditions. The finite element numerical simulation technology is used to simulate the material die forging process. The key point is to introduce the microstructure model into the die forging simulation, so that the grain size and phase volume fraction can be realized while observing the macroscopic physical field distribution. It can be seen that the model can accurately predict the average grain size and component size of the lower anti-torque arm of Ti-7333 alloy. By analyzing the macro-physical fields and the distribution of microstructure in the forging process, the process parameters of hot die forging and isothermal die forging of lower anti-torque arm can be well optimized. Accordingly, it is understood that the in the large deformation regions, dislocation density is high and grain size of β phase is small. Compared with hot die forging, the differences of the temperature, β grain size, and volume fraction of phases of workpiece will be reduced under isothermal die forging. In particular, increasing the deformation temperature and the pushing speed at the same time can reduce the differences of β grain size of workpiece under hot die forging. On the contrary, improving deformation temperature and decreasing pushing speed and friction coefficient at the same time can reduce the differences of β grain size and volume fraction of α phase of workpiece under isothermal die forging.
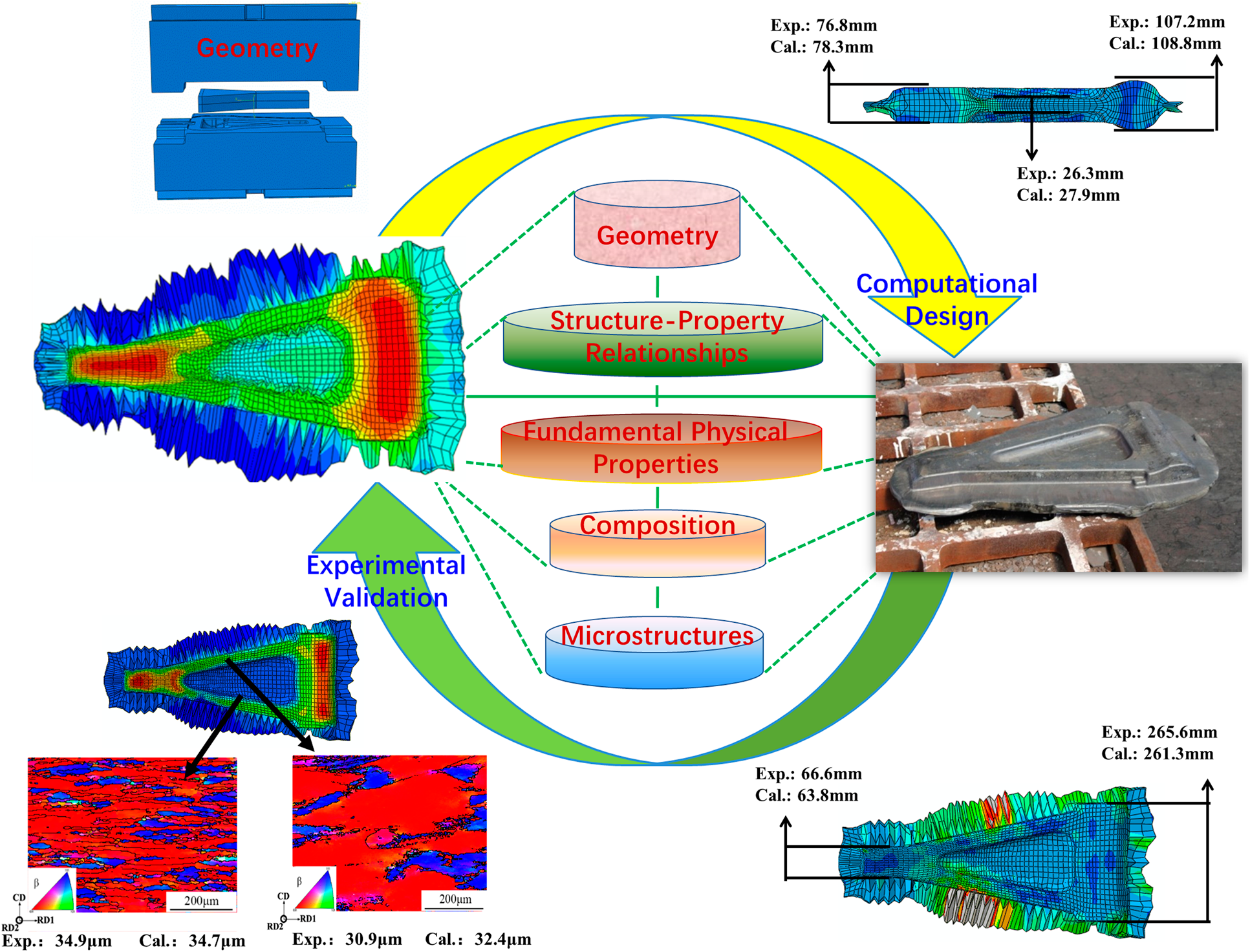
Figure 6: Digital-twin designing and manufacturing approaches for the Ti7333 landing gear torque arm.
Mg alloys
Mg and its alloys, being one kind of light-weight materials, are particularly attractive for transportation, electronic devices, and biocompatible/biodegradable applications [Reference Wang, Tang, Shang, Wang, Li, Wang, Zhu, Wei, Wang, Darling, Mathaudhu, Wang, Ren, Hui, Kecskes, Li and Liu95]. One of the key challenges is to simultaneously improve their low-temperature ductility and strength [Reference Wang, Tang, Shang, Wang, Li, Wang, Zhu, Wei, Wang, Darling, Mathaudhu, Wang, Ren, Hui, Kecskes, Li and Liu95, Reference Lu96, Reference Wu, Chan, Zhu, Sun and Lu97, Reference Yu, Qi, Mishra, Li and Minor98]. As shown in Fig. 7, our previous works have comprehensively revealed the electronic and atomic basis for toughening and strengthening of Mg alloys via the interface engineering approach [Reference Zhou, Wang, Liu, Arroyave and Horstemeyer24, Reference Wang, Shang, Wang, Darling, Kecskes, Mathaudhu, Hui and Liu56, Reference Wang, Wang, Shang, Darling, Kim, Tang, Kou, Mathaudhu, Hui, Li, Kecskes and Liu67, Reference Shang, Wang, Zhou, Wang, Darling, Kecskes, Mathaudhu and Liu93, Reference Wang, Tang, Shang, Wang, Li, Wang, Zhu, Wei, Wang, Darling, Mathaudhu, Wang, Ren, Hui, Kecskes, Li and Liu95, Reference Wang, Shang, Wang, Kim, Darling, Kecskes, Mathaudhu, Hui and Liu99, Reference Wang, Shang, Wang, Mei, Darling, Kecskes, Mathaudhu, Hui and Liu100]. The local HCP-FCC phase transformations of SFs and LPSOs have been identified theoretically and experimentally by bonding charge density and high-resolution transmission microscope [Reference Wang, Tang, Shang, Wang, Li, Wang, Zhu, Wei, Wang, Darling, Mathaudhu, Wang, Ren, Hui, Kecskes, Li and Liu95], both of which will enable the low-temperature ductility of Mg alloys [Reference Wang, Wang, Shang, Darling, Kim, Tang, Kou, Mathaudhu, Hui, Li, Kecskes and Liu67, Reference Jian, Cheng, Xu, Yuan, Tsai, Wang, Koch, Zhu and Mathaudhu101]. The contributions of the local FCC-type fault layers to the thermodynamic properties and the bonding structures of Mg are revealed. It is noted that those elements highlighted in the periodic table by an abbreviation and blue background in Fig. 7 indicate the typical/classical solutes considered in the development/manufacturing of advanced Mg alloy. Accordingly, the effects of those solute atoms on the ESF, EWF, dislocation width, bonding structures, twinnability, and ideal strength are comprehensively studied [Reference Shang, Wang, Zhou, Wang, Darling, Kecskes, Mathaudhu and Liu93, Reference Wang, Tang, Shang, Wang, Li, Wang, Zhu, Wei, Wang, Darling, Mathaudhu, Wang, Ren, Hui, Kecskes, Li and Liu95, Reference Wang, Shang, Wang, Mei, Darling, Kecskes, Mathaudhu, Hui and Liu100]. Similarly, recent works have reported segregations and twin boundary pinning to strengthen Mg alloys [Reference Nie, Zhu, Liu and Fang102, Reference Zhao, Chen, Wilson, Liu and Nie103].
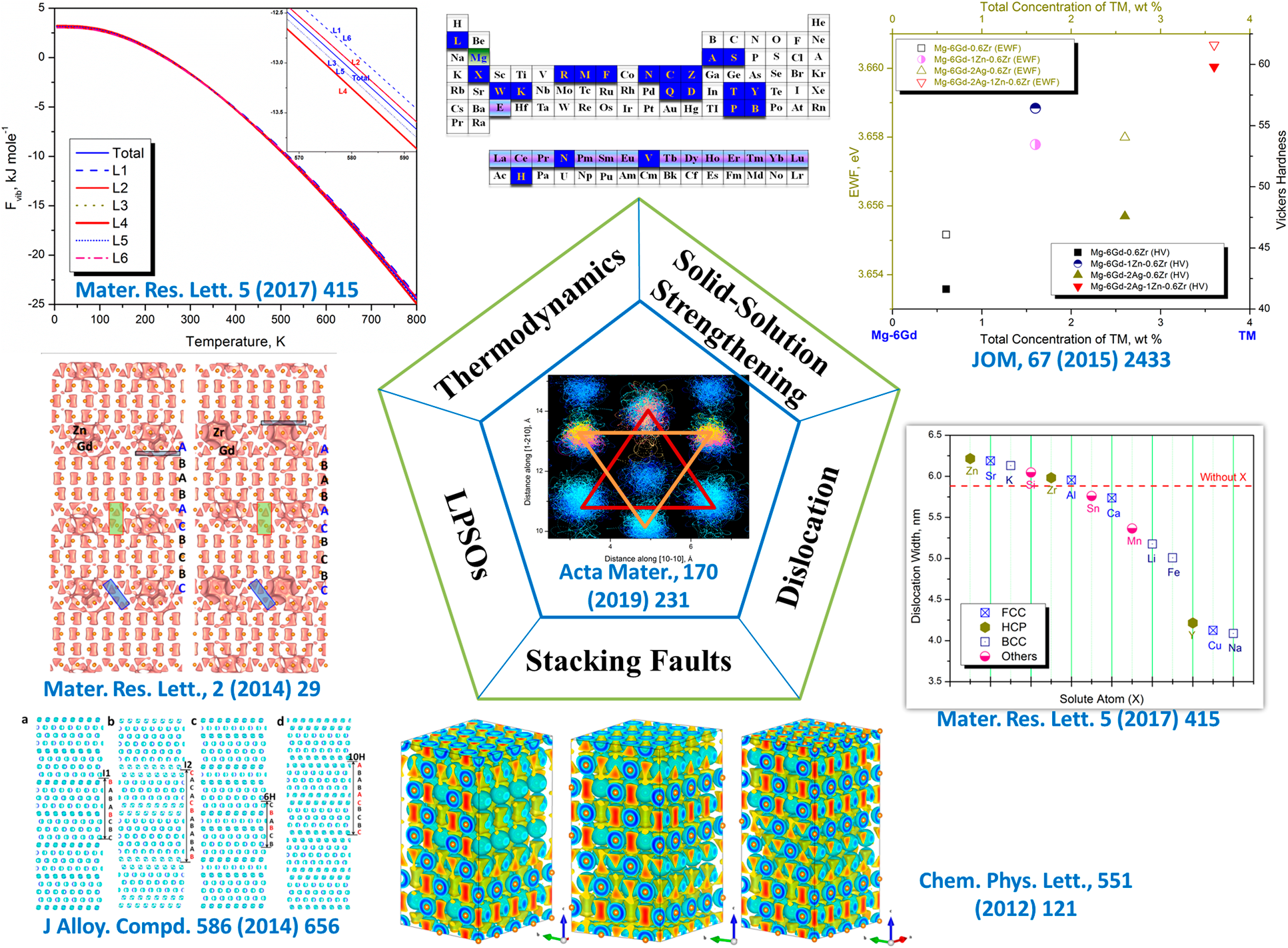
Figure 7: Strengthening and toughening strategies of Mg alloys based on first-principles properties repository.
Moreover, lattice strain engineering has been considered as a key strategy in discovering advanced materials. Through yielding a local lattice distortion near solute atoms, a dislocation-free plastic deformation can form structural faults [Reference Wang, Tang, Shang, Wang, Li, Wang, Zhu, Wei, Wang, Darling, Mathaudhu, Wang, Ren, Hui, Kecskes, Li and Liu95, Reference Saito, Furuta, Hwang, Kuramoto, Nishino, Suzuki, Chen, Yamada, Ito, Seno, Nonaka, Ikehata, Nagasako, Iwamoto, Ikuhara and Sakuma104]. Based on our proposed atomic array models in HCP structure, the severe lattice distortions mediate the HCP-to-FCC transformation via atomic shuffling process, which is captured by the atomic trajectories from AIMD calculations [Reference Wang, Tang, Shang, Wang, Li, Wang, Zhu, Wei, Wang, Darling, Mathaudhu, Wang, Ren, Hui, Kecskes, Li and Liu95]. That is the reasons why we proposed the strategy to strength the Mg alloys via the self-dispersed nano-lamellar faults [Reference Wang, Wang, Shang, Darling, Kim, Tang, Kou, Mathaudhu, Hui, Li, Kecskes and Liu67]. It is understood that solute-induced lattice distortion can serve as one of many possible design principles for advanced Mg alloys, which is different from the classical shear deformation via either dislocation or affine/alias deformation [Reference Wang, Tang, Shang, Wang, Li, Wang, Zhu, Wei, Wang, Darling, Mathaudhu, Wang, Ren, Hui, Kecskes, Li and Liu95, Reference Saito, Furuta, Hwang, Kuramoto, Nishino, Suzuki, Chen, Yamada, Ito, Seno, Nonaka, Ikehata, Nagasako, Iwamoto, Ikuhara and Sakuma104].
Co-based superalloys
In line with the aforementioned interface engineering strategy, the novel advanced Co-based superalloys can be potentially discovered by tailoring the local bonding environments, the macroscopic elastic and plastic properties, phase stabilities/transformations, structural defects and so on [Reference Ball55, Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Zhang, Li, Wang, Li, Tang, Wang, Kou, Shang, Wang, Kecskes, Hui, Feng and Liu62]. As shown in Fig. 8, the physical natures of local phase transformations of APB and SISF have been characterized clearly by bonding charge density, which are L12 → D022 and L12 → D019, respectively. In particular, the tetrahedral bonds of the L12 matrix are the same as the measured FCC Al ones [Reference Nakashima, Smith, Etheridge and Muddle66], which transform into the “S” shape in the APB and the rode-type of HCP in SISF [Reference Wang, Shang, Wang, Darling, Mathaudhu, Hui and Liu69]. The effects of solutes on the energy of APB and SISF, the modulus, the lattice distortion, the magnetism, and the bonding are comprehensively investigated. On the one hand, it is highlighted that the lattice distortion optimization caused by solutes has been recognized as a key approach in the development of advanced structural materials [Reference Jiang, Wang, Wu, Liu, Chen, Yao, Gault, Ponge, Raabe, Hirata, Chen, Wang and Lu105, Reference Vitos, Abrikosov and Johansson106, Reference Meher, Carroll, Pollock and Carroll107, Reference Zenk, Neumeier, Stone and Goken109]. A positive lattice misfit (>) [Reference Sato, Omori, Oikawa, Ohnuma, Kainuma and Ishida110, Reference Titus, Mottura, Babu Viswanathan, Suzuki, Mills and Pollock111] will yield a better high-temperature strength than otherwise similar alloys with a negative misfit, which is probably an important factor making the strengthened Co-based superalloys for future high-temperature applications [Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Mughrabi112]. Due to a higher thermal expansion coefficient of the matrix, the alloys with a positive lattice misfit should exhibit a decreased misfit at the aging temperature [Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Povstugar, Zenk, Li, Choi, Neumeier, Dolotko, Hoelzel, Göken and Raabe113]. At the temperatures close to the solvus temperature, the misfit drops even further due to the beginning dissolution of and the corresponding compositional changes of [Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Povstugar, Zenk, Li, Choi, Neumeier, Dolotko, Hoelzel, Göken and Raabe113]. The lattice misfit can be adjusted effectively through controlling the partitioning of alloying elements in the Co-based superalloys [Reference Meher, Carroll, Pollock and Carroll107, Reference Meher, Yan, Nag, Dye and Banerjee114], which also yield anomalous bonding structures [i.e., “from heart to hand” feature of Ti and Ta in Co3TM in Fig. 8(a)], thus to optimize the deformation behaviors.
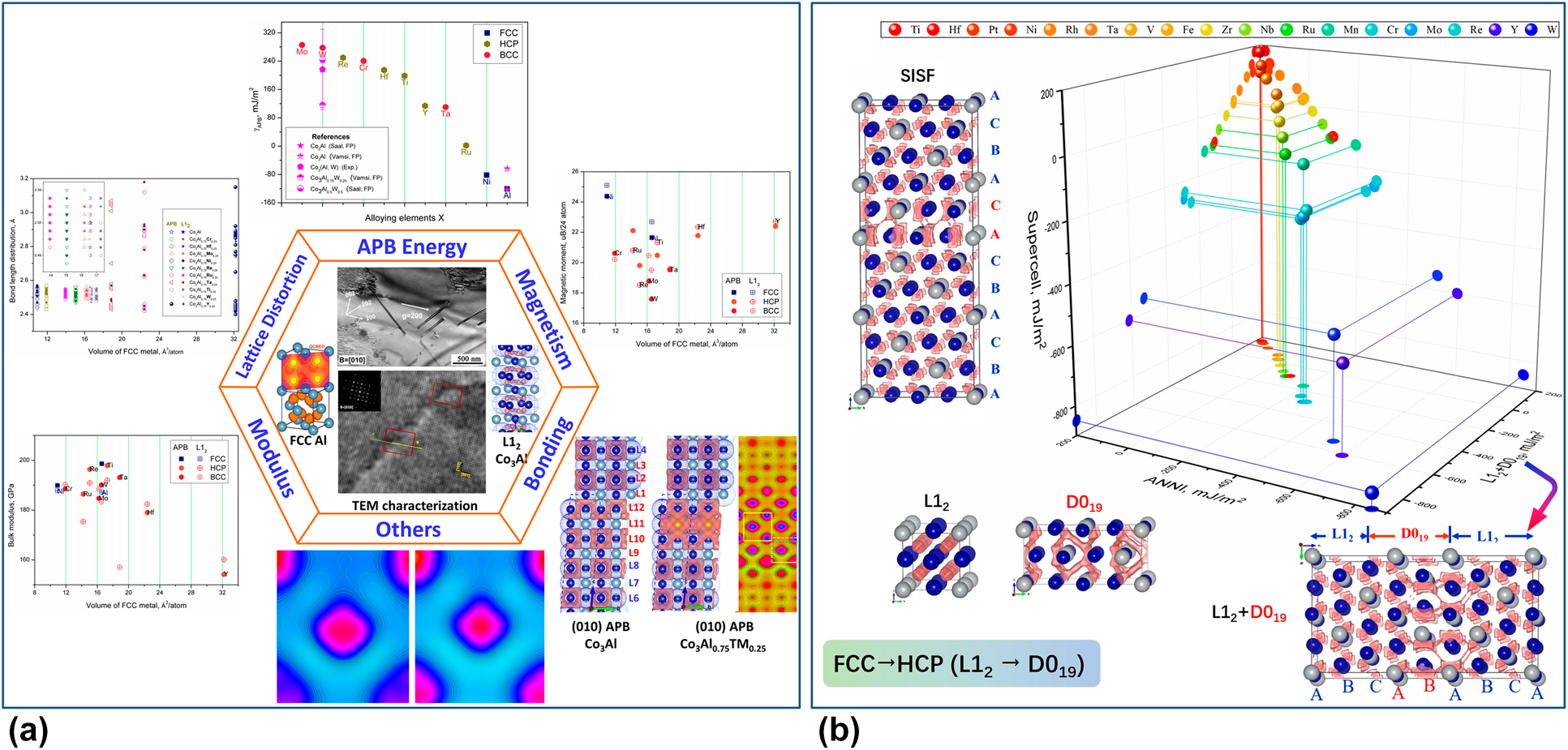
Figure 8: When defect is a pathway to improve stability of Co-based superalloys: (a) atomic and electronic basis for the solutes strengthened L12 Co3(Al, TM) APB [Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57] and (b) comparisons of E SF values of Co3TM calculated by the SISF-supercell method, the ANNI model, and the L12 + D019 model [Reference Zhang, Li, Wang, Li, Tang, Wang, Kou, Shang, Wang, Kecskes, Hui, Feng and Liu62].
On the other hand, it is critical to understand/control the planar defect segregation behaviors of the solute atoms at the fault layers, which dominate the shearing mechanisms during creep. As shown in Fig. 8(b), the results of ESISF via the ANNI model are consistent with the classical. SISF-supercell method utilized in first-principles calculations provides the approach to efficiently distinguish various planar faults and predict their corresponding energies, such as SISF [Reference Denteneer and Haeringen115, Reference Chandran and Sondhi116], SESF [Reference Denteneer and Haeringen115, Reference Chandran and Sondhi116], and APB [Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Colinet and Pasturel117], etc. [Reference Zhang, Li, Wang, Li, Tang, Wang, Kou, Shang, Wang, Kecskes, Hui, Feng and Liu62]. It can be seen that interface/defect engineering has been one of the important strategies in the development of advanced materials. In fact, interfaces/defects not only affect the local bonding environment/strength at the atomic scale but also play a dominant role adjusting the macroscopic elastic and plastic properties. Motivated by the discovery of novel stable L12 Co3(Al,W) compound a decade ago [Reference Sato, Omori, Oikawa, Ohnuma, Kainuma and Ishida110] and the recent work entitled “When Defects are not Defects” [Reference Krasheninnikov58], a great amount of efforts have been made in the investigations of its structural defects and phase transformations, the transformations of which dominate the performance of the material in service. Our recent works [Reference Wang, Xue, Zhang, Shang, Wang, Darling, Kecskes, Li, Hui, Feng and Liu57, Reference Zhang, Li, Wang, Li, Tang, Wang, Kou, Shang, Wang, Kecskes, Hui, Feng and Liu62] suggest that controlling energies of planar defects (such as stacking faults and APBs) by alloying is critical for the development of advanced superalloys.
Refractory high entropy alloys
Lattice distortion/misfit has been set as one of the four hypotheses in the discovery of advanced high-entropy alloys, which can be caused by the atomic radius differences among various solute/solvent and the local chemical orders/disorders [Reference Wang, Wang, Lin, Zou, Wu, Hu, Shang, Darling, Wang, Hui, Li, Kecskes, Liaw and Liu49, Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51]. It is understood that local chemical orders play an important role in the mechanical properties of HEA, such as serrations, strengthening, and functional applications [Reference George, Raabe and Ritchie33, Reference Wang, Wang, Lin, Zou, Wu, Hu, Shang, Darling, Wang, Hui, Li, Kecskes, Liaw and Liu49, Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51, Reference Ding, Zhang, Chen, Fu, Chen, Chen, Gu, Wei, Bei, Gao, Wen, Li, Zhang, Zhu, Ritchie and Yu118, Reference Gao, Miracle, Maurice, Yan, Zhang and Hawk119, Reference Yeh and Lin120]. Recently, improved experimental and theoretical tools to study short-range ordering effects have been highlighted [Reference George, Raabe and Ritchie33]. Referring to the classical special quasirandom structures [Reference Zunger, Wei, Ferreira and Bernard121, Reference Jiang, Wolverton, Sofo, Chen and Liu122, Reference Gao, Yeh, Liaw and Zhang123], the cluster-plus-glue-atom model can not only yield the identical random structures but also provide the ordered ones, supporting a strategy to reveal the effects of order–disorder configurational transitions on the properties of HEAs [Reference Wang, Wang, Lin, Zou, Wu, Hu, Shang, Darling, Wang, Hui, Li, Kecskes, Liaw and Liu49, Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51]. As shown in Fig. 9(a), the configurational transitions are constructed for these BCC equiatomic refractory HEAs. In the view of Δρ, the local lattice distortion caused by various group of elements results in the so-called weak spots, where there is few bonding electrons constructing the loose-packed regions. For example, the regions enriched of Zr atoms with the larger atomic radius in configuration R1 form weak spots [Reference Dahmen, Ben-Zion and Uhl124], the bonding strength of which is very low. On the contrary, the tightly bonded clusters with higher value of Δρ display the physical nature of the solid-solution strengthening mechanism, contributing to the high strength of RHEAs [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51]. Moreover, the responses of weak spot and cluster to the elastic and the plastic deformation are different. While the former of which results in a slip avalanche via the sudden burst of atomic motion [Reference Dahmen, Ben-Zion and Uhl124] and structural rejuvenation [Reference Ma125], the latter one is hard to slip/shear.
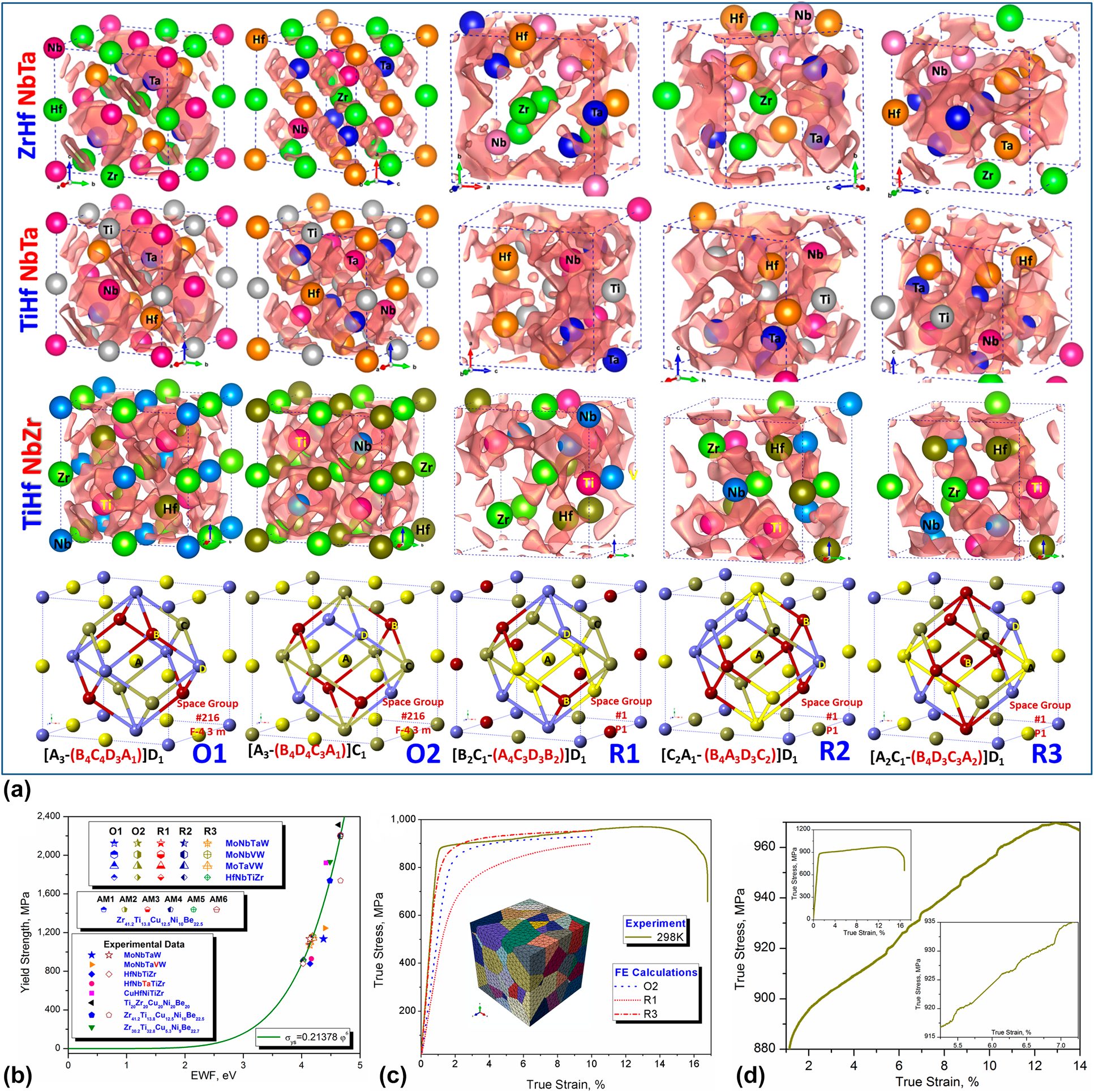
Figure 9: The atomic and electronic basis for the configurational transition dominated properties of RHEAs: (a) various microstates/configurations of ZrHfNbTa, TiHfNbTa, and TiHfNbZr alloys; (b) power-law scaled yield strength of HEAs [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51]; and (c, d) the configurational transition dominated mechanical properties and the experimental serration behavior of TiHfNbZr [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51].
Furthermore, VEC has been treated as one key design principle in the discovery of new HEAs [Reference Guo and Liu64, Reference Troparevsky, Morris, Kent, Lupini and Stocks126, Reference Zhang, Zuo, Tang, Gao, Dahmen, Liaw and Lu127, Reference Poletti and Battezzati128]. For example, the formation of FCC- or BCC-type HEAs in a given multicomponent system can be estimated by the value of the VEC, which is >7.5 to 8 and <6 to 7.5 for FCC and BCC HEAs, respectively [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51, Reference Guo and Liu64, Reference Zhang, Zuo, Tang, Gao, Dahmen, Liaw and Lu127, Reference Poletti and Battezzati128]. Based on the aforementioned comparisons between VEC and EWF shown in Fig. 3, these two VEC criteria locate at the VIIB–VIIIB and the IVB–VIIB group elements constituting the equiatomic HEAs. In line with Fig. 9(b), it is worth to mention that the power-law scaled mechanical properties, including hardness, yield strength, and Young's modulus, can be predicted in terms of EWF, which have been validated in pure elements [Reference Hua and Li129, Reference Hua and Li130], Al alloys [Reference Wang, Darling, Wang, Shang, Kecskes, Hui and Liu70], HEAs [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51], and vit-1 metallic glass [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51]. Since the slip/shear process consists electronic redistributions during breaking and reforming chemical bonds, the variations in the first neighbor atoms in the slip planes would result in different microstates as shown in Fig. 9(a). Correspondingly, their effects on the yield strength of TiHfNbZr are presented in Fig. 9(c), which contribute to the experimentally observed serration behaviors in Fig. 9(d). Therefore, the atomic structure–dominated elastic and plastic properties can be predicted and revealed comprehensively by atoms and electrons [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51]. It is expected that the integrations of multiscale simulations with the aid of principles/criteria, such as enthalpy of mixing (ΔH), entropy of mixing (ΔH), lattice distortion/misfit or atomic size difference (δ), and VEC/EWF, will be an effective strategy accelerating the discovery of advanced HEAs [Reference Wang, Shang, Wang, Han, Darling, Wu, Xie, Senkov, Li, Hui, Dahmen, Liaw, Kecskes and Liu51, Reference Senkov, Miller, Miracle and Woodward131, Reference Gao and Alman132].
Al alloys
Because of their the high strength-to-weight ratio, recyclability, and resistance to corrosion, age-hardenable Al alloys are widely utilized in the aerospace, transport, automotive, and shipbuilding industries [Reference Guan, Sun, Wang, Gao, Zou, Wang, Tang, Kou, Wang, Hou, Gao, Ma and Li133]. With the quick development of the high-speed railway and the service of the China Railway High-speed (CRH) series for more than a decade, it is extremely important to manage/maintain those trains in service environmental conditions [Reference Wang, Zou, Lin, Tang, Zhang, Sun, Guan, Tang, Wang, Kou, Gao, Song, Ma and Li61, Reference Guan, Sun, Wang, Gao, Zou, Wang, Tang, Kou, Wang, Hou, Gao, Ma and Li133]. Accordingly, the corrosion resistance of the utilized Al alloys is recommended to be tested strictly, such as the pitting corrosion, intergranular corrosion, and stress corrosion cracking. Since hydrogen is usually coupled with the structural defects (including vacancy, solutes, interfaces, and boundaries), hydrogen embrittlement (HE) has been considered as a serious industrial problem, overcompensating the energy cost to form defects, reducing the ductility and resulting in the brittle fracture [Reference Xie, Li, Li, Wang, Gumbsch, Sun, Ma, Li and Shan134, Reference Zhou, Marchand, McDowell, Zhu and Song135, Reference Zhou and Song136, Reference Wolverton, Ozolin and Asta137, Reference Lu and Kaxiras138, Reference Song and Curtin139, Reference Gunaydin, Barabash, Houk and Ozolins140]. It is noted that the stress corrosion cracking and corrosion fatigue/fracture of high-strength Al alloys always involve hydrogen [Reference Ben Ali, Tanguy and Estevez141].
Figure 10 displays our recent works of the hydrogen-mediated failure of Al, Al98H2, and Al95H5 alloys by classical molecular dynamics simulations, investigating the effect of hydrogen on their deformation behavior and crack propagation under axial tension at a strain rate of 1 × 10−9 s−1. As shown in Fig. 10(a), there is a severe lattice strain at the crack tip, which is characterized in terms of von Mises strain. During the tensile plastic deformation, the crack propagation paths (two groups of slip planes in red) of Al follow Schmid's law, yielding the angle between the tensile force and the slip plane to be 45° and obtaining the maximum shear stresses along the slip planes. With the improved concentration of H, there will be less shear/slip bands or dislocations in the Al matrix. Since the snapshots of Al, Al98H2, and Al95H5 are selected with the same running time, it can been seen that both the cracking distance and the thickness of slip bands are improved with the enhanced concentration of H, indicating the hydrogen-assisted cracking and the accelerated cracking rate. Through enlarging atomic radius of H atoms, higher than that of Al atoms, the trapped hydrogen activated crack propagation and slip of Al98H2 are represented obviously in Fig. 10(b). It can be seen that the enriched H atoms along the slip bands endure the higher von Mises strain and the bonding strength of which is weaker than the Al–Al bond [Reference Wang, Zou, Lin, Tang, Zhang, Sun, Guan, Tang, Wang, Kou, Gao, Song, Ma and Li61], dominating the cracking propagation paths. Thus, H atoms are always captured in each slip plane, especially at the tip highlighted by those ellipses in Fig. 10(c). Therefore, with electronic and atomic structures, the mechanisms and models of hydrogen-induced damage in structural metal materials can be revealed clearly [Reference Hou, Kong, Wu, Song and Liu53, Reference Wang, Zou, Lin, Tang, Zhang, Sun, Guan, Tang, Wang, Kou, Gao, Song, Ma and Li61, Reference Georgiou, Cevallos, Van der Donck, Drees, Meersschaut, Panagopoulos and Celis142, Reference Tanguy, Bayle, Dif and Magnin143, Reference Isayev, Oses, Toher, Gossett, Curtarolo and Tropsha144]. Recently, first-principles modeling of anisotropic anodic dissolution of metals and alloys in corrosive environments reveals a formula to specify the relationship between the electrode potential and the current density by considering the basic parameters of surface energy density and work function, providing a promising perspective for designing better corrosion-resistant alloys [Reference Isayev, Oses, Toher, Gossett, Curtarolo and Tropsha144].

Figure 10: Hydrogen-mediated failure of Al and Al–H alloys and its electronic basis. (a) Effect of hydrogen on the deformation behavior and crack propagation of Al, Al98H2, and Al95H5 under axial tension at a strain rate of 1 × 10−9 s−1. (b) The trapped hydrogen activated crack propagation and slip of Al98H2 presenting an obvious contrast by enlarging atomic radius of H atoms than those of Al atoms. (c) The trapped hydrogen at the tip of the dislocation and the von Mises strain is utilized to present the BGR gradient colors with minimum and maximum values of 0.001 and 0.9, respectively.
Summary and outlooks
In summary, a brief review of our case studies of data-driven ICME for intelligently discovering/optimizing advanced structural metal materials is presented, which include the light-weight materials (Ti, Mg, and Al alloys), RHEAs, and superalloys for high temperature applications. The basic bonding in terms of topology and electronic structures is recommended to be considered as the building blocks/units constructing the microstructures of advanced materials. Data—the basic unit building block of database and advanced computational algorithms such as machine learning, data mining, deep learning, and artificial intelligence—have been recognized as the third essential digital resource in the I3M beside the natural mineral materials and the financial funds. The flow chain of “Data-Cyber-Knowledge-Wisdom” presents the inheritable feature of the data in the frameworks of “Materials Genome,” which is also highlighted in the Data-driven ICME designing paradigm of advanced materials. It is expected that the integration of knowledge-based multiscale modeling/simulations and the machine-learning self-knowledge base, materials design and discovery will be further accelerated [Reference Umehara, Stein, Guevarra, Newhouse, Boyd and Gregoire145, Reference Gubernatis and Lookman146]. More duties are called to contribute the developments of data repositories, platforms/standards, and the training of next-generation workforce. Particularly, training our next-generation workforce will be the long-term strategic plan of both MGI/MGE and ICME, thus to support the enrollment in traditional advanced materials programs and to propel the field forward [Reference Pollock, Allison, Backman, Boyce, Gersh, Holm, Lesar, Long, IV, Schirra, Whitis and Woodward1, Reference de Pablo, Jackson, Webb, Chen, Moore, Morgan, Jacobs, Pollock, Schlom, Toberer, Analytis, Dabo, DeLongchamp, Fiete, Grason, Hautier, Mo, Rajan, Reed, Stevanovic, Suntivich, Thornton and Zhao10, Reference Liu, Furrer, Kosters and Holmes36, 147]. It is worth mentioning that several objectives/aspects were addressed for preparing the current, emerging, and future workforce, who are responsible for implementing the activities for accelerating discovery, development and deployment of new materials by utilizing their wide cross-section of knowledge and capabilities from other fields, i.e., chemistry, physics, biology, mathematics, computer science, data science, statistics, and information technology [Reference Pollock, Allison, Backman, Boyce, Gersh, Holm, Lesar, Long, IV, Schirra, Whitis and Woodward1, Reference de Pablo, Jackson, Webb, Chen, Moore, Morgan, Jacobs, Pollock, Schlom, Toberer, Analytis, Dabo, DeLongchamp, Fiete, Grason, Hautier, Mo, Rajan, Reed, Stevanovic, Suntivich, Thornton and Zhao10, Reference Liu, Furrer, Kosters and Holmes36, 147]. Through building advanced algorithms in the development of a promising digital fabricating approach to address the present and future challenges, it is believed that the digital-twin intelligent manufacturing era is coming soon [Reference Wang, Li, Liu and Liu2].
Acknowledgments
The authors acknowledge the financial supports from the National Key Research and Development Program of China (2016YFB0701304, 2016YFB0701303, 2018YFB0703801, and 2018YFB0703802), the National Natural Science Foundation of China (Grant No. 51690163), National Science and Technology Major Project (2017-VI-0014-0086), CRRC Tangshan Co., Ltd. (Contract No. 201750463031), Science Challenge Project (Contract No. TZZT2019-D1.5), project of SKL-AMM-USTB (Grant No. 2016-Z07), and Fundamental Research Funds for the Central Universities in China (G2016KY0302). Y. Zhang would like to thank the financial supports from the Seed Foundation of Innovation and Creation for Graduate Students at Northwestern Polytechnical University (ZZ2019081).













