Article contents
On the competition between the stress-induced formation of martensite and dislocation plasticity during crack propagation in pseudoelastic NiTi shape memory alloys
Published online by Cambridge University Press: 17 July 2017
Abstract
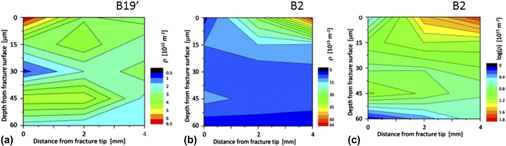
The present work addresses the competition between dislocation plasticity and stress-induced martensitic transformations in crack affected regions of a pseudoelastic NiTi miniature compact tension specimen. For this purpose X-ray line profile analysis was performed after fracture to identify dislocation densities and remnant martensite volume fractions in regions along the crack path. Special emphasis was placed on characterizing sub fracture surface zones to obtain depth profiles. The stress affected zone in front of the crack-tip is interpreted in terms of a true plastic zone associated with dislocation plasticity and a pseudoelastic zone where stress-induced martensite can form. On unloading, most of the stress-induced martensite transforms back to austenite but a fraction of it is stabilized by dislocations in both, the irreversible martensite and the surrounding austenite phase. The largest volume fraction of the irreversible or remnant martensite along with the highest density of dislocations in this phase was found close to the primary crack-tip. With increasing distance from the primary crack-tip both, the dislocation density and the volume fraction of irreversible martensite decrease to lower values.
Keywords
Information
- Type
- Articles
- Information
- Journal of Materials Research , Volume 32 , Issue 23: Focus Issue: Mechanical Properties and Microstructure of Advanced Metallic Alloys—in Honor of Prof. Haël Mughrabi PART A , 14 December 2017 , pp. 4433 - 4442
- Copyright
- Copyright © Materials Research Society 2017
Footnotes
Contributing Editor: Mathias Göken
Dedicated to the 80th Birthday of Professor Haël Mughrabi.
This author was an editor of this journal during the review and decision stage. For the JMR policy on review and publication of manuscripts authored by editors, please refer to http://www.mrs.org/editor-manuscripts/.
A previous error in this article has been corrected. For details, see 10.1557/jmr.2017.459
References
REFERENCES
A correction has been issued for this article:
- 23
- Cited by
Linked content
Please note a has been issued for this article.


