Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hoagland, R. G.
Daw, M. S.
Foiles, S. M.
and
Baskes, M. I.
1990.
The Nature of Crack Tip Fields in Atomic Scale Models of Aluminum.
MRS Proceedings,
Vol. 193,
Issue. ,
Sawamura, Akitaka
Watanabe, Yoichi
and
Yamamoto, Ryoichi
1991.
Computer Aided Innovation of New Materials.
p.
335.
Hoagland, R.G.
Daw, M.S.
and
Hirth, J.P.
1991.
Some aspects of forces and fields in atomic models of crack tips.
Journal of Materials Research,
Vol. 6,
Issue. 12,
p.
2565.
Huang, Y.M.
Spence, J.C.H.
Sankey, Otto F.
and
Adams, G.B.
1991.
The influence of internal surfaces on the (2 × 1) shuffle and glide cleavage reconstructions for Si(111).
Surface Science,
Vol. 256,
Issue. 3,
p.
344.
Rice, J. R.
Beltz, G. E.
and
Sun, Y.
1992.
Topics in Fracture and Fatigue.
p.
1.
Baskes, M.I.
Hoagland, R.G.
and
Needleman, A.
1992.
Summary report: computational issues in the mechanical behavior of metals and intermetallics.
Materials Science and Engineering: A,
Vol. 159,
Issue. 1,
p.
1.
Rice, James R.
1992.
Dislocation nucleation from a crack tip: An analysis based on the Peierls concept.
Journal of the Mechanics and Physics of Solids,
Vol. 40,
Issue. 2,
p.
239.
Hoagland, R.G.
and
Heinisch, H.L.
1992.
An atomic simulation of the influence of hydrogen on the fracture behavior of nickel.
Journal of Materials Research,
Vol. 7,
Issue. 8,
p.
2080.
Foiles, Stephen M.
1992.
Equilibrium Structure and Properties of Surfaces and Interfaces.
p.
89.
Sasaki, Naoya
Iwasaki, Tomio
Chiba, Norimasa
Abe, Yasuo
and
Ishikawa, Yuichi
1993.
Molecular Dynamics Simulation of Tensile Deformation of Iron Single Crystals Including Thermal Effect.
JSME international journal. Ser. A, Mechanics and material engineering,
Vol. 36,
Issue. 1,
p.
50.
Daw, Murray S.
Foiles, Stephen M.
and
Baskes, Michael I.
1993.
The embedded-atom method: a review of theory and applications.
Materials Science Reports,
Vol. 9,
Issue. 7-8,
p.
251.
Sun, Yuemin
Beltz, Glenn E.
and
Rice, James R.
1993.
Estimates from atomic models of tension-shear coupling in dislocation nucleation from a crack tip.
Materials Science and Engineering: A,
Vol. 170,
Issue. 1-2,
p.
67.
Michalske, Terry A.
and
Bunker, Bruce C.
1993.
A Chemical Kinetics Model for Glass Fracture.
Journal of the American Ceramic Society,
Vol. 76,
Issue. 10,
p.
2613.
Zhou, S. J.
Carlsson, A. E.
and
Thomson, Robb
1994.
Crack blunting effects on dislocation emission from cracks.
Physical Review Letters,
Vol. 72,
Issue. 6,
p.
852.
Hoagland, R.G.
and
Liu, Yi
1994.
Environmental effects on crack tip processes at the atomic level.
Materials Science and Engineering: A,
Vol. 176,
Issue. 1-2,
p.
219.
Hoagland, Richard G.
1994.
On the energetics of dislocation emission from a crack tip in nickel containing hydrogen.
Journal of Materials Research,
Vol. 9,
Issue. 7,
p.
1805.
Sun, Yuemin
and
Beltz, Glenn E.
1994.
Dislocation nucleation from a crack tip: A formulation based on anisotropic elasticity.
Journal of the Mechanics and Physics of Solids,
Vol. 42,
Issue. 12,
p.
1905.
Kitagawa, Hiroshi
1994.
Fracture Mechanisms in Atomic Scale : Atomic Simulation of Crack Tip Processes.
Journal of the Society of Mechanical Engineers,
Vol. 97,
Issue. 907,
p.
459.
Zhang, Y. W.
Wang, T. C.
and
Tang, Q. H.
1995.
Simulation of nucleation and emission of dislocations by molecular-dynamics method.
Journal of Applied Physics,
Vol. 77,
Issue. 6,
p.
2393.
Grujicic, M.
and
Dang, P.
1995.
Molecular dynamics embedded atom method simulations of crack-tip transformation toughening in FeNi austenite.
Materials Science and Engineering: A,
Vol. 199,
Issue. 2,
p.
173.
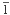 10)-[110], and (
10)-[110], and (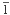 10)-[111]. The first two models behaved in a brittle fashion as dislocation emission did not occur for reasons associated with the use of periodic boundary conditions parallel to the crack front. For the models which remained atomically sharp, the positions of the atoms near the crack tip in equilibrium configurations are different from the linear elastic predictions but, to first order, retain an r1/2 dependence, with smaller K, and with the origin displaced behind the physical crack tip. This near tip region is also observed to be elastically softer than in the far field. Dislocation emission readily proceeds in the (
10)-[111]. The first two models behaved in a brittle fashion as dislocation emission did not occur for reasons associated with the use of periodic boundary conditions parallel to the crack front. For the models which remained atomically sharp, the positions of the atoms near the crack tip in equilibrium configurations are different from the linear elastic predictions but, to first order, retain an r1/2 dependence, with smaller K, and with the origin displaced behind the physical crack tip. This near tip region is also observed to be elastically softer than in the far field. Dislocation emission readily proceeds in the (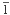 10)-[111] model by the sequential emission of partials with attendant nonzero uz displacements. The blunting is characterized by the creation of two corner defects that separate as emission occurs and relaxation of the strains in the region initially confronted by the crack tip. Additional features of the results are discussed.
10)-[111] model by the sequential emission of partials with attendant nonzero uz displacements. The blunting is characterized by the creation of two corner defects that separate as emission occurs and relaxation of the strains in the region initially confronted by the crack tip. Additional features of the results are discussed.
