No CrossRef data available.
Published online by Cambridge University Press: 11 September 2014
Twisted K-theory on a manifold X, with twisting in the 3rd integral cohomology, is discussed in the case when X is a product of a circle 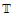 and a manifold M. The twist is assumed to be decomposable as a cup product of the basic integral one form on
and a manifold M. The twist is assumed to be decomposable as a cup product of the basic integral one form on 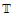 and an integral class in H2(M,ℤ). This case was studied some time ago by V. Mathai, R. Melrose, and I.M. Singer. Our aim is to give an explicit construction for the twisted K-theory classes using a quantum field theory model, in the same spirit as the supersymmetric Wess-Zumino-Witten model is used for constructing (equivariant) twisted K-theory classes on compact Lie groups.
and an integral class in H2(M,ℤ). This case was studied some time ago by V. Mathai, R. Melrose, and I.M. Singer. Our aim is to give an explicit construction for the twisted K-theory classes using a quantum field theory model, in the same spirit as the supersymmetric Wess-Zumino-Witten model is used for constructing (equivariant) twisted K-theory classes on compact Lie groups.