Hostname: page-component-6bb9c88b65-bcq64 Total loading time: 0 Render date: 2025-07-19T07:22:46.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Simplicial homotopy in semi-abelian categories

Published online by Cambridge University Press:  04 September 2008

Tim Van der Linden
Tim Van der Linden
Affiliation:
tvdlinde@vub.ac.beVakgroep WiskundeVrije Universiteit BrusselPleinlaan 21050 Brussel, Belgium
Get access

Abstract

We study Quillen's model category structure for homotopy of simplicial objects in the context of Janelidze, Márki and Tholen's semi-abelian categories. This model structure exists as soon as 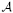is regular Mal'tsev and has enough regular projectives; then the fibrations are the Kan fibrations of S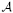. When, moreover, 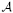is semi-abelian, weak equivalences and homology isomorphisms coincide.

Keywords

semi-abelian categorymodel categorysimplicial object

Information

Type
Research Article
Information
Journal of K-Theory , Volume 4 , Issue 2 , October 2009 , pp. 379 - 390
Copyright
Copyright © ISOPP 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Barr, M.. Exact categories, Exact categories and categories of sheaves, Lecture notes in mathematics 236, Springer, 1971, 1–120Google Scholar
2.Borceux, F. and Bourn, D.. Mal'cev, protomodular, homological and semi-abelian categories, Mathematics and its Applications 566, Kluwer Academic Publishers, 2004Google Scholar
3.Bourn, D., Normalization equivalence, kernel equivalence and affine categories, Category Theory, Proceedings Como 1990 (Carboni, A., Pedicchio, M. C., and Rosolini, G., eds.), Lecture notes in mathematics 1488, Springer, 1991, 43–62Google Scholar
4.Bourn, D.. Mal'cev categories and fibration of pointed objects, Appl. Categ. Struct. 4 (1996), 307–327Google Scholar
5.Bourn, D.. 3 × 3 lemma and protomodularity, J. Algebra 236 (2001), 778–795Google Scholar
6.Carboni, A., Kelly, G. M., and Pedicchio, M. C., Some remarks on Maltsev and Goursat categories, Appl. Categ. Struct. 1 (1993), 385–421CrossRefGoogle Scholar
7.Carboni, A., Lambek, J., and Pedicchio, M. C., Diagram chasing in Mal'cev categories, J. Pure Appl. Alg. 69 (1991), 271–284Google Scholar
8.Everaert, T. and der Linden, T. Van. Baer invariants in semi-abelian categories II: Homology, Theory Appl. Categ. 12 (2004), no. 4, 195–224Google Scholar
9.Janelidze, G., Márki, L., and Tholen, W.. Semi-abelian categories, J. Pure Appl. Algebra 168 (2002), 367–386Google Scholar
10.Quillen, D. G.. Homotopical algebra, Lecture notes in mathematics 43, Springer, 1967Google Scholar
11.Weibel, Ch. A., An introduction to homological algebra, Cambridge studies in advanced mathematics 38, Cambridge University Press, 1997Google Scholar