Article contents
Remarks on Murre's conjecture on Chow groups
Published online by Cambridge University Press: 30 October 2013
Abstract
For certain product varieties, Murre's conjecture on Chow groups is investigated. More precisely, let k be an algebraically closed field, X be a smooth projective variety over k and C be a smooth projective irreducible curve over k with function field K. Then we prove that if X (resp. XK) satisfies Murre's conjectures (A) and (B) for a set of Chow-Künneth projectors {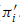 , 0 ≤ i ≤ 2dim X} of X (resp. for {(
, 0 ≤ i ≤ 2dim X} of X (resp. for {(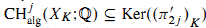 )K} of XK) and if for any j,
)K} of XK) and if for any j, 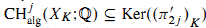 , then the product variety X × C also satisfies Murre's conjectures (A) and (B). As consequences, it is proved that if C is a curve and X is an elliptic modular threefold over k (an algebraically closed field of characteristic 0) or an abelian variety of dimension 3, then Murre's conjecture (B) is true for the fourfold X × C.
, then the product variety X × C also satisfies Murre's conjectures (A) and (B). As consequences, it is proved that if C is a curve and X is an elliptic modular threefold over k (an algebraically closed field of characteristic 0) or an abelian variety of dimension 3, then Murre's conjecture (B) is true for the fourfold X × C.
Information
- Type
- Research Article
- Information
- Journal of K-Theory , Volume 12 , Issue 1: Nanjing Special Issue on K-theory, number theory and geometry , August 2013 , pp. 3 - 14
- Copyright
- Copyright © ISOPP 2013
References
- 3
- Cited by

