Article contents
Relative Zariski Open Objects
Published online by Cambridge University Press: 31 January 2012
Abstract
In [TV], Bertrand Toën and Michel Vaquié define a scheme theory for a closed monoidal category ( ,⊗, 1) One of the key ingredients of this theory is the definition of a Zariski topology on the category of commutative monoidal objects in
,⊗, 1) One of the key ingredients of this theory is the definition of a Zariski topology on the category of commutative monoidal objects in  . The purpose of this article is to prove that under some hypotheses, Zariski open subobjects of affine schemes can be classified almost as in the usual case of rings (ℤ-mod,⊗,ℤ). The main result states that for any commutative monoidal object A in
. The purpose of this article is to prove that under some hypotheses, Zariski open subobjects of affine schemes can be classified almost as in the usual case of rings (ℤ-mod,⊗,ℤ). The main result states that for any commutative monoidal object A in  , the locale of Zariski open subobjects of the affine scheme Spec(A) is associated to a topological space whose points are prime ideals of A and whose open subsets are defined by the same formula as in rings. As a consequence, we can compare the notions of scheme over
, the locale of Zariski open subobjects of the affine scheme Spec(A) is associated to a topological space whose points are prime ideals of A and whose open subsets are defined by the same formula as in rings. As a consequence, we can compare the notions of scheme over 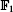 in [D] and in [TV].
in [D] and in [TV].
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © ISOPP 2011
References
- 5
- Cited by

