Published online by Cambridge University Press: 02 January 2014
We examine the theory of connective algebraic K-theory, 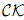 , defined by taking the −1 connective cover of algebraic K-theory with respect to Voevodsky's slice tower in the motivic stable homotopy category. We extend
, defined by taking the −1 connective cover of algebraic K-theory with respect to Voevodsky's slice tower in the motivic stable homotopy category. We extend 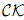 to a bi-graded oriented duality theory
to a bi-graded oriented duality theory 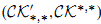 when the base scheme is the spectrum of a field k of characteristic zero. The homology theory
when the base scheme is the spectrum of a field k of characteristic zero. The homology theory  may be viewed as connective algebraic G-theory. We identify
may be viewed as connective algebraic G-theory. We identify 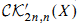 for X a finite type k-scheme with the image of
for X a finite type k-scheme with the image of 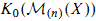 in
in 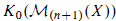 , where
, where 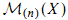 is the abelian category of coherent sheaves on X with support in dimension at most n; this agrees with the (2n,n) part of the theory of connective algebraic K-theory defined by Cai. We also show that the classifying map from algebraic cobordism identifies
is the abelian category of coherent sheaves on X with support in dimension at most n; this agrees with the (2n,n) part of the theory of connective algebraic K-theory defined by Cai. We also show that the classifying map from algebraic cobordism identifies 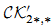 with the universal oriented Borel-Moore homology theory
with the universal oriented Borel-Moore homology theory 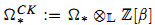 having formal group law u + υ − βuυ with coefficient ring ℤ[β]. As an application, we show that every pure dimension d finite type k-scheme has a well-defined fundamental class [X]CK in ΩdCK(X), and this fundamental class is functorial with respect to pull-back for l.c.i. morphisms.
having formal group law u + υ − βuυ with coefficient ring ℤ[β]. As an application, we show that every pure dimension d finite type k-scheme has a well-defined fundamental class [X]CK in ΩdCK(X), and this fundamental class is functorial with respect to pull-back for l.c.i. morphisms.