Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Androulidakis, Iakovos
and
Zambon, Marco
2013.
Smoothness of holonomy covers for singular foliations and essential isotropy.
Mathematische Zeitschrift,
Vol. 275,
Issue. 3-4,
p.
921.
Debord, Claire
and
Skandalis, Georges
2014.
Adiabatic groupoid, crossed product byR+⁎and pseudodifferential calculus.
Advances in Mathematics,
Vol. 257,
Issue. ,
p.
66.
Androulidakis, Iakovos
2014.
Laplacians and spectrum for singular foliations.
Chinese Annals of Mathematics, Series B,
Vol. 35,
Issue. 5,
p.
679.
Androulidakis, Iakovos
and
Zambon, Marco
2017.
Almost regular Poisson manifolds and their holonomy groupoids.
Selecta Mathematica,
Vol. 23,
Issue. 3,
p.
2291.
Lescure, Jean-Marie
and
Vassout, Stéphane
2017.
Fourier integral operators on Lie groupoids.
Advances in Mathematics,
Vol. 320,
Issue. ,
p.
391.
Debord, Claire
and
Skandalis, Georges
2018.
Lie groupoids, exact sequences, Connes–Thom elements, connecting maps and index maps.
Journal of Geometry and Physics,
Vol. 129,
Issue. ,
p.
255.
Androulidakis, Iakovos
and
Skandalis, Georges
2019.
A Baum–Connes conjecture for singular
foliations.
Annals of K-Theory,
Vol. 4,
Issue. 4,
p.
561.
Carrillo Rouse, Paulo
and
So, Bing Kwan
2020.
K-theory and Index Theory for Some Boundary Groupoids.
Results in Mathematics,
Vol. 75,
Issue. 4,
Zambon, Marco
2022.
Singular subalgebroids.
Annales de l'Institut Fourier,
Vol. 72,
Issue. 6,
p.
2109.
Mohsen, Omar
2024.
Tangent groupoid and tangent cones in sub-Riemannian geometry.
Duke Mathematical Journal,
Vol. 173,
Issue. 16,
Laurent-Gengoux, Camille
Louis, Ruben
and
Ryvkin, Leonid
2025.
Advances in Poisson Geometry.
p.
123.

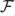 ). In the current paper we construct the analytic index of an elliptic operator as a
). In the current paper we construct the analytic index of an elliptic operator as a 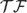 on
on 