Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Garkusha, Grigory
2016.
Algebraic Kasparov K-theory, II.
Annals of K-Theory,
Vol. 1,
Issue. 3,
p.
275.
Garkusha, Grigory
2018.
Comparing motives of smooth algebraic varieties.
Comptes Rendus. Mathématique,
Vol. 356,
Issue. 11-12,
p.
1100.
Garkusha, Grigory
2019.
Reconstructing rational stable motivic homotopy theory.
Compositio Mathematica,
Vol. 155,
Issue. 7,
p.
1424.
Druzhinin, Andrei
and
Kolderup, Håkon
2020.
Cohomological correspondence categories.
Algebraic & Geometric Topology,
Vol. 20,
Issue. 3,
p.
1487.
Garkusha, Grigory
2023.
Correspondences and stable homotopy theory.
Transactions of the London Mathematical Society,
Vol. 10,
Issue. 1,
p.
124.

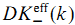
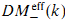 . To each smooth
. To each smooth 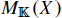 is associated in the category
is associated in the category