Published online by Cambridge University Press: 16 May 2012
Multirings are objects like rings but with multi-valued addition. In the present paper we extend results of E. Becker and others concerning orderings of higher level on fields and rings to orderings of higher level on hyperfields and multirings and, in the process of doing this, we establish higher level analogs of the results previously obtained by the second author. In particular, we introduce a class of multirings called ℓ-real reduced multirings, define a natural reflection A ⇝ Qℓ-red(A) from the category of multirings satisfying 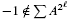 to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined.
to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined.