No CrossRef data available.
Published online by Cambridge University Press: 07 January 2008
Let k be a number field and let X be a smooth, projective and geometrically integral k-variety. We show that, if the geometric Néron-Severi group of X is torsion-free, then the Galois cohomology group 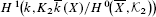 is finite. Previously this group was only known to have a finite exponent. We also obtain a vanishing theorem for this group, showing in particular that it is trivial if X belongs to a certain class of abelian varieties with complex multiplication. The interest in the above cohomology group stems from its connection to the torsion subgroup of the Chow group CH2(X) of codimension 2 cycles on X. In the last section of the paper we record certain results on curves which must be familiar to all specialists in this area but which we have not formerly seen in print.
is finite. Previously this group was only known to have a finite exponent. We also obtain a vanishing theorem for this group, showing in particular that it is trivial if X belongs to a certain class of abelian varieties with complex multiplication. The interest in the above cohomology group stems from its connection to the torsion subgroup of the Chow group CH2(X) of codimension 2 cycles on X. In the last section of the paper we record certain results on curves which must be familiar to all specialists in this area but which we have not formerly seen in print.