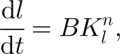Introduction
Attempts to model the mechanics of crevassing and to propose a criterion for crevasse formation go back to the pioneering work of Reference NyeNye (1957). Recently, there has been renewed interest in crevassing, especially in the context of ice-shelf fracturing (Reference RistRist and others, 1999, 2002). Following the seminal work of Reference SmithSmith (1976), these recent investigations of crevassing (Reference Van der VeenVan der Veen, 1998b; Reference RistRist and others, 1999, 2002; Reference Nath and VaughanNath and Vaughan, 2003) were based on linear elastic fracture mechanics (LEFM). In these studies, crevasses are considered as mode I cracks formed under tension, and a crevasse initiation criterion is given by KI = KIC , where KI is the mode I stress intensity factor associated with the initiation flaw (sometimes called “starter crack”) and KIC the fracture toughness of the ice. KI , which measures the intensity of the stress field surrounding the crack, is proportional to σ × l 1/2 where σ is the applied stress and l is the crack length. Most of the works cited above aimed to analyze the stability (or instability) of crevasse propagation through depth, and especially to derive a maximum crevasse depth corresponding to the depth at which crack propagation is arrested by the overburden stress. The crevasse arrest criterion was chosen to be either KI ≤ 0 (Reference SmithSmith, 1976; Reference Rist, Sammonds, Oerter and DoakeRist and others, 2002) or KI ≤ KIC (Reference Van der VeenVan der Veen, 1998b; Reference Nath and VaughanNath and Vaughan, 2003).
This LEFM approach to crevassing does, however, come up against some problems, including:
-
(i) The visco-plastic flow of glaciers a priori precludes a straightforward application of LEFM, which is based on a linear elastic rheology. In the case of materials with a non-linear behaviour, more sophisticated criteria for crack propagation have been proposed, with partial success (see, e.g., Reference MiannayMiannay, 1998).
-
(ii) Within the LEFM framework, the initiation of crevassing requires the presence of large sharp flaws within the ice, large enough for the condition KI ≥ KIC to be exceeded under tensile stresses which are probably no greater than a few hundred kPa. This implies flaw sizes of the order of a few tens of cm or larger (see further below). This problem was stressed by Reference Nath and VaughanNath and Vaughan (2003) who were uncertain that such flaws would exist in firn.
-
(iii) The crevasse arrest criteria proposed above are probably misleading, as the stress intensity factor at arrest, though non-zero, is always lower than the stress intensity factor at initiation (Reference Ravi-Chandar and BouchaudRavi-Chandar, 2001). Moreover, with crack propagation speeds close to the body wave speed (i.e. the situation encountered when KI ≥ KIC ), dynamic effects have to be taken into account to correctly predict the arrest condition (Reference Ravi-Chandar and BouchaudRavi Chandar, 2001).
Some observations related to ice terminus in temperate glaciers or to iceberg calving and ice-shelf disintegration are also difficult to reconcile with the LEFM description of crevasse initiation and propagation. Reference FlotronFlotron (1977) and Reference RöthlisbergerRöthlisberger (1977) reported an acceleration of the horizontal displacement across a crevasse (i.e. a proxy of crevasse opening, itself related to crevasse depth) whose propagation led to the fall of a large ice block from a hanging glacier. This acceleration showed a singular behaviour as approaching the failure time tf :

where υ is the velocity of the horizontal displacement across the crevasse and A and m are parameters. If the velocity–time evolution can be extrapolated and m is stable through time (see further below), the breaking-off time may be tentatively predicted. This acceleration, observed over periods of the order of several months, can hardly be explained by an unstable crack growth at speeds close to the body wave speed. Keeping the LEFM framework, one may argue that these low speeds could result from an averaging over time of many step-like critical (KI > KIC ) increments, but this would raise the problem of multiple crack arrests. This point is discussed later in this paper. Using finite-element calculations, Reference IkenIken (1977) modelled such acceleration by a stepwise crack extension coupled with viscous flow. The crevasse is assumed to propagate when the tensile stress at its tip, estimated from a finite-element analysis of viscous flow, becomes greater than a critical value, σI > σC, and stops when this stress becomes compressive, σI ≤ 0. Then the increasing overhang of the ice block due to ice flow again raises the stress to tensile values large enough to allow further propagation. These crack-initiation and crack-arrest criteria are very crude, as they do not take into account the depth of the crevasse and suffer from the limitations described in point (iii) above. Recently, Reference Pralong, Funk and LüthiPralong and others (2003) proposed an alternative explanation of this acceleration using damage-mechanics concepts. In damage mechanics, the effective stress σeff is expressed as σeff = σ/(1 – D), where the apparent applied stress σ is the applied force divided by an apparent section, and the damage D itself increases with increasing effective stress. Such positive feedback necessarily leads to a finite-time singularity of the form of Equation (1). Implementing such a mechanism into a numerical code, Reference Pralong, Funk and LüthiPralong and others (2003) reproduced in their ice-terminus modelling an acceleration of crevasse opening before breaking-off. However, damage mechanics was designed to model situations where the damage is spatially homogeneous within the material. The relevance of damage mechanics for the case where an ice terminus collapse is related to the propagation of one or a few large crevasses can therefore be questioned. The mechanism proposed by Reference Pralong, Funk and LüthiPralong and others (2003) might only capture some aspects of the process.
Crevasse propagation supposedly plays a key role in iceberg calving (Reference Van der VeenVan der Veen, 1998a; Reference Hanson and HookeHanson and Hooke, 2000) and the stability of ice shelves (Reference Vaughan and DoakeVaughan and Doake, 1996). Satellite imagery reveals propagation of cracks in ice shelves over several km to several hundred km in several years (see, e.g., Reference Fricker, Young, Allison and ColemanFricker and others, 2002), i.e. average crack speeds of several mm s–1 or below, as well as a strong acceleration during the last days preceding the calving of the associated giant icebergs. These average propagation rates are orders of magnitude lower than body wave speeds (around 3300 m s–1 for polycrystalline ice). At a more global scale, a common feature of ice-shelf retreats by iceberg calving is a marked acceleration during the final stages (Reference Vaughan and DoakeVaughan and Doake, 1996).
Here I propose an alternative mechanism, namely sub-critical crack growth, to account for these low crevasse-propagation rates and for these accelerations in the later stages of failure.
Subcritical Crack Propagation in Materials
In many different materials such as rocks (Reference AtkinsonAtkinson, 1979; Reference Das and ScholzDas and Scholz, 1981), ceramics or glass (Reference Wiederhorn, Bradt, Hasselman and LangeWiederhorn, 1978; Reference Gy and BouchaudGy, 2001), it has been observed that a crack can propagate at speeds much lower than the body wave speed even when the stress intensity factor is lower than the fracture toughness. This is subcritical growth, which has also been discussed as “quasi-static growth” or “static fatigue” (Reference Gy and BouchaudGy, 2001). Three regimes can be observed:
-
(i) For KI below a lower limit K 0, no crack growth occurs.
-
(ii) For K 0 ≤ KI < KIC , subcritical crack growth occurs, characterized by a crack growth rate given by:

where l is the crack size, and B and n are parameters.
-
(iii) For KI ≥ KIC , i.e. the classical LEFM situation, unstable propagation occurs at speeds representing a significant fraction of the body wave speed.
Fracture toughness of glacier ice varies with ice density and temperature. For low-porosity ice, a value of KIC around 150 kPa m1/2 is often reported (see, e.g., Reference Rist, Sammonds, Oerter and DoakeRist and others, 2002). Note that a possible scale effect on KIC has been reported for lake ice (Reference Dempsey, DeFranco, Adamson and MulmuleDempsey and others, 1999a) and sea ice (Reference Dempsey, DeFranco, Adamson and MulmuleDempsey and others, 1999b), KIC rising from about 120 kPa m1/2 at a scale of 0.5m to about 250 kPa m1/2 at scales larger than 10 m.
The experimental estimation of K 0 is generally very difficult, and the existence of such a threshold is perhaps questionable, as the growth rates near K 0 are extremely slow. In any case, K 0 is likely to be only a small fraction of the toughness KIC . Equation (2) is an empirical relation, and the reported values of the exponent n are generally large, lying between 10 and 50 with a modal value around 15 (Reference Gy and BouchaudGy, 2001). These large exponents imply that accurate measurements are needed to distinguish this subcritical behaviour from a step function. When observed, Equation (2) remains generally valid over a very large range of crack velocities covering several orders of magnitude. Three broad categories of mechanisms have been proposed to explain sub-critical crack growth: plastic flow, chemical reactions, and diffusion processes related either to the motion of atoms and vacancies near the crack tip or to the transport of reactive species (Reference Wiederhorn, Bradt, Hasselman and LangeWiederhorn, 1978; Reference AtkinsonAtkinson, 1979). These thermally activated processes explain why B in Equation (2) is an Arrhenius temperature-dependent parameter. No experimental data exist on subcritical crack growth for ice. However, as suggested by Reference Rist, Sammonds, Oerter and DoakeRist and others (2002), this possibility is at least worth exploring.
The conditions encountered on glaciers—visco-plastic flow, high homologous temperatures in the case of temperate glaciers, presence of chemical impurities—are favourable factors for the mechanisms listed above. As an example, stress concentrations at the crevasse tip may increase the segregation of solutes concentrated along grain boundaries and favour local melting at the tip. Below, I explore the likely behaviour of a crevasse experiencing subcritical crack growth and show how it could explain some of the observations listed in the introduction, especially for ice terminus and calving. This is done for a few simplified situations for which analytical expressions of the evolution of the stress intensity factor with depth have been given in the literature or can be proposed. Although these calculations are certainly oversimplifications, they do illustrate a possible effect of subcritical growth on crevasse formation. It is not my intention to rule out the possibility of critical crevasse propagation in glaciers (as evidenced by icequakes; Reference Neave and SavageNeave and Savage, 1970) or of other mechanisms, such as damage accumulation (Reference Pralong, Funk and LüthiPralong and others, 2003), to explain the acceleration of propagation before ice terminus collapse or calving.
Subcritical Crevasse Growth
I consider the plane problem of an isolated crevasse of depth l (its “length”) within an ice layer (the “glacier”) of thickness H, as shown in Figure 1. I will consider the evolution of the crevasse as described by the three regimes of tensile cracking detailed above (no cracking, subcritical, critical). The problem remains to integrate Equation (2), i.e. to know the evolution of the stress intensity factor KI with the crevasse length l. KI depends on the stress profile along the faces of the crevasse, which itself depends on many factors: the rheology of the ice, the surface slope of the glacier, the boundary conditions, etc. In what follows, I will consider a few typical and simplified situations for which a stress profile can be estimated. I do not consider the presence of water within the crevasse (in sufficient amount to counteract the effect of the overburden stress), possible interactions between crevasses, an evolution of ice properties with depth (e.g. density, fracture toughness), or bottom crevasses within ice shelves. However, once one is able to estimate the stress profile along the crevasse faces for these more sophisticated situations (see, e.g., Reference SmithSmith (1976) and Reference Van der VeenVan der Veen (1998b) for the presence of water within the crevasse; Reference Rist, Sammonds, Murrell, Meredith, Oerter and DoakeRist and others (1996) and Reference Van der VeenVan der Veen (1998b) for an evolution of density from top firn to bottom ice; and Reference SmithSmith (1976) and Reference Sassolas, Pfeffer and AmadeiSassolas and others (1996) for crevasse interactions), the analysis of subcritical crevassing is straightforward using the same procedure as described below.

Fig. 1. Surface crevasse within a glacier: geometry and notation of the plane problem considered.
Surface crevasse in a glacier
I consider first the classical situation of a surface crevasse within a glacier where the stress profile normal to its faces is the superposition of two terms (Fig. 1):
-
(i) a tensile stress resulting from flow gradients, σt. Following many others (Reference SmithSmith, 1976; Reference Van der VeenVan der Veen, 1998b; Reference RistRist and others, 1999), the simplifying assumption is made that σt is constant throughout the ice thickness. Reference Nath and VaughanNath and Vaughan (2003) argued that a constant strain rate throughout the thickness is more realistic. If the material properties change with depth (e.g. the porosity for firn, or if the crevasse extends into the deeper layers in a glacier where the non-linear softening of the ice due to horizontal shearing becomes important), this implies that σt varies with depth. This aspect is neglected here.
-
(ii) the compressive overburden stress which increases with depth according to σp = ρi gz, where ρ i is the density of ice (917 kg m–3) and z the depth below the glacier surface.
These two terms act against each other, leading to discussion of various crack-arrest criteria in the literature (and consequently different maximum crevasse depth): σt = σp (Reference NyeNye, 1957), KI = 0 (Reference SmithSmith, 1976) or KI = KIC (Reference Van der VeenVan der Veen, 1998b).
Following Reference SmithSmith (1976), I first neglect the finite thickness of the glacier (H → +∞). For a plane problem (Fig. 1), KI is:

where
![]() represents the opening term associated with the tensile stress σt and
represents the opening term associated with the tensile stress σt and
![]() the closing term associated with the compressive overburden stress.
the closing term associated with the compressive overburden stress.
For a semi-elliptical crevasse which does not cross the entire glacier width, the expression of KI would be similar, with numerical coefficients depending on the aspect ratio of the ellipse (Reference BroekBroek, 1982). The combination of Equations (2) and (3) leads to a differential equation whose integration, using standard numerical integration tools such as the fourth-order Runge–Kutta algorithm, determines the evolution of the crevasse with time, i.e. l = f(t). Two examples are given in Figures 2 and Reference Broek3. In the absence of data on sub-critical cracking in ice, n was set to a value of 15 close to the modal value observed for rocks or ceramics (Reference AtkinsonAtkinson, 1979; Reference Gy and BouchaudGy, 2001). The parameter B was fixed to 1017 for stresses expressed in MPa, lengths in m and time in s (so B is expressed in MPa−n m1−n/2 s–1). This value falls within the (very large) range of values reported for rocks or ceramics with similar exponent n. Once again, the calculations presented below were performed to illustrate the mechanisms, without intention to predict the quantitative behaviour of a real crevasse in ice. Note, moreover, that the B values reported for other materials depend on different factors, including temperature, and are given with a large uncertainty. The integration started at time t 0 = 0 with a crevasse depth l 0 of 3 cm. Under a given tensile stress at the surface, an initial flaw is required for the stress intensity factor KI to overcome the lower limit K 0. As noted above, in materials where subcritical cracking is documented, K 0, when it can be estimated, is much lower than the fracture toughness KIC .

Fig. 2. Subcritical crevassing of a surface crevasse within a glacier (n = 15; B = 1017; σt = 50 kPa). (a) Evolution of the crevasse depth, l, with time, showing a sigmoidal behaviour. Note the logarithmic vertical scale for the main graph and the linear vertical scale for the inset. (b) Evolution of the stress intensity factor KI with the crevasse depth: the critical condition KI = KIC is never attained during the crevasse life.
Figure 2a shows the evolution of crevasse depth with time for a tensile stress σt = 50 kPa. A sigmoidal behaviour is observed. First, the crevasse deepens very slowly, albeit at an increasing rate. This acceleration is driven by an increase of KI
as l increases in the upper part of the glacier where the tensile term of Equation (3),
![]() , largely overcomes the effect of the overburden stress
, largely overcomes the effect of the overburden stress
![]() . This acceleration continues until an inflexion point at time t
i ≈ 167 days at which the crevasse is deep enough to sense the effect of the over-burden stress. Then the crevasse decelerates towards a maximum depth l
max of about 9 m. This maximum depth is set by the condition KI
= K
0, reached after a time infinitely long if K
0 = 0. Whereas l
max is independent of n or B, t
i is dependent on those parameters. As the growth rate is proportional to B (Equation (2)), a B value 10 times larger (respectively 10 times lower) decreases (respectively increases) t
i by a factor of 10. t
i also strongly depends on n: for the case described above, an n value of 14 (respectively 16) decreases (respectively increases) t
i by a factor of 54 compared to n = 15. Figure 2b shows the evolution of the stress intensity factor KI
with the crevasse depth l. KI
, which reaches a maximum value of K
max = 114:5 kPa m1/2 at about 3 m depth, never attains the critical toughness of 150 kPa m1/2, therefore excluding critical crevasse growth. K
max and the corresponding depth are calculated from the condition dKI
/dl = 0:
. This acceleration continues until an inflexion point at time t
i ≈ 167 days at which the crevasse is deep enough to sense the effect of the over-burden stress. Then the crevasse decelerates towards a maximum depth l
max of about 9 m. This maximum depth is set by the condition KI
= K
0, reached after a time infinitely long if K
0 = 0. Whereas l
max is independent of n or B, t
i is dependent on those parameters. As the growth rate is proportional to B (Equation (2)), a B value 10 times larger (respectively 10 times lower) decreases (respectively increases) t
i by a factor of 10. t
i also strongly depends on n: for the case described above, an n value of 14 (respectively 16) decreases (respectively increases) t
i by a factor of 54 compared to n = 15. Figure 2b shows the evolution of the stress intensity factor KI
with the crevasse depth l. KI
, which reaches a maximum value of K
max = 114:5 kPa m1/2 at about 3 m depth, never attains the critical toughness of 150 kPa m1/2, therefore excluding critical crevasse growth. K
max and the corresponding depth are calculated from the condition dKI
/dl = 0:
In this example, we are not faced with the problem of the definition of a crack-arrest criterion: the same physics (sub-critical growth) holds for the accelerating as for the decelerating phase towards an asymptotic depth, supposedly without dynamical effects. The maximum crevasse-growth speed
![]() is reached at t = t
i As most of the time is spent in the earlier stages of growth, the inflexion time t
i strongly depends on the initial flaw size l
0, whereas the other characteristics such as the maximum velocity, the maximum stress intensity factor or the asymptotic depth do not.
is reached at t = t
i As most of the time is spent in the earlier stages of growth, the inflexion time t
i strongly depends on the initial flaw size l
0, whereas the other characteristics such as the maximum velocity, the maximum stress intensity factor or the asymptotic depth do not.
As n is large, the crevasse evolution is very sensitive to the tensile stress σt. Figure 3 shows the crevasse evolution for a tensile stress of 80 kPa. Although the accelerating phase is similar, the time-scale as well as the final evolution strongly differ. Starting again from l = l 0 = 3 cm, the maximum crack speed predicted from subcritical cracking would be reached after about 1226 s (<3.5 hours; see Fig. 3a). However, the critical condition KI = KIC is fulfilled just before the inflexion point is reached, at l ≈ 1 m (Fig. 3b). Therefore, one expects the “initiation” of unstable crevasse propagation from this depth. In that case, we are again faced with the problem of crack arrest that sets the maximum depth.

Fig. 3. Subcritical crevassing of a surface crevasse within a glacier (n = 15; B = 1017; σt = 80 kPa). (a) Evolution of the crevasse depth, l, with time. (b) Evolution of the stress intensity factor KI with the crevasse depth: the critical condition KI = KIC is fulfilled when the crevasse reaches a depth of about 1 m.
For the same loading case (Fig. 1), Reference Van der VeenVan der Veen (1998b) took into account the finite thickness of the glacier, H. He found that the effect of H is to increase the stress intensity factor KI (l) as a non-linear function of the ratio l/H. This implies an increase of the crevasse growth rates and consequently a decrease of t i. However, when the ratio between the crevasse depth at t i and H is small, the effect of H on subcritical crevasse evolution is very small. For the numerical examples given above (n = 15; B = 1017) and a glacier thickness around 100 m, the numerically computed crevasse evolutions are almost indistinguishable from the infinite-thickness solutions for t < t i. This is not incompatible with a strong effect of H in the critical regime (KI ≥ KIC ), especially for large tensile stresses allowing large maximum depths (Reference Van der VeenVan der Veen, 1998b). It will be shown later that H may also have a significant effect in the case of a crevasse located near a glacier terminus.
From this crude exploration of possible subcritical crevassing within glaciers, some interesting points can be stressed. The first one concerns the origin of initial sharp flaws that are needed to initiate crevasse propagation under a tensile stress σt. Surface stresses have never been directly measured on glaciers; rather they are estimated from strain rates (themselves calculated from surface velocity measurements) and a visco-plastic ice-flow law (e.g. Reference NyeNye, 1957; Reference RistRist and others, 1999). As an example, tensile stresses around 100–200 kPa are rather large values. From a phenomenological approach analyzing the association between the presence of crevasses and measured strain rates, from which stresses were deduced, Reference VaughanVaughan (1993) reported critical tensile stress values in the range 90–200 kPa for crevassing within glaciers. Within a classical LEFM framework, for a tensile stress σ t of 150 kPa and a toughness of 150 kPa m1/2, an initial flaw size of 26 cm at the glacier surface would be required to initiate unstable propagation (KI = KIC and KI given by Equation (3)). As stressed previously by Reference RistRist and others (1999) and Reference Nath and VaughanNath and Vaughan (2003), the existence of such large sharp flaws is questionable. Small microcracks of length of the order of the grain-size can form within the ice as the result of dislocation pile-ups during plastic flow (Reference FrostFrost, 2001) or grain-boundary sliding (Reference Weiss and SchulsonWeiss and Schulson, 2000). However, these microflaws would not be long enough to initiate unstable propagation. Larger flaws such as voids may exist within glacier ice, but these blunted features would require larger stresses to be activated than sharp cracks.
Subcritical cracking is an elegant alternative to solve this problem. As the lower threshold for subcritical propagation K 0 is always a small fraction of the material toughness KIC , subcritical crevassing would allow crevasse initiation and propagation from much smaller initial flaw sizes. Using the same set of parameters as before (n = 15; B = 1017), a microcrack of 3 mm (i.e. a reasonable order of magnitude for an average grain-size within glacier ice) under a tensile stress t of 150 kPa will grow up to the LEFM critical value of 26 cm in 35 days. Once again, these time-scales are only given to illustrate the mechanisms and have no real quantitative meaning, as the parameters n and B are unknown.
As illustrated above with the examples of Figures 2 and 3, the crevasse evolution is very sensitive to σt. Consequently, a small initial flaw subjected to a (constant) small tensile stress will not reach a significant depth within reasonable time, whereas it would rapidly fulfil the conditions for unstable propagation under (constant) large stress. However, as these flaws move with the glacier flow and therefore experience a changing stress history, it is easy to imagine a scenario where a small flaw of a few mm initially grows under a relatively large tensile stress to a depth of the order of a few tens of cm to a few metres and then, as it moves downwards, experiences smaller tensile stress under which it may propagate subcritically down to an asymptotic depth without reaching the critical condition KI = KIC .
Hanging glacier, glacier terminus and iceberg calving
The situation of a crevasse located close to a glacier terminus, near the end of a hanging glacier or an ice shelf (Fig. 4), is now considered. This is the situation studied by Reference IkenIken (1977). In this situation, it is easy to understand that the effect of the overburden stress is greatly reduced, if not negligible. The stress profile along the faces of the crevasse depends on many parameters: surface slope of the glacier, distance of the crevasse from the calving face, geometry of the bottom of the glacier (with possible overhangs), the “substrate” (rocks, or water for ice shelves), etc. Reference HughesHughes (1992) used beam theory to estimate these stress profiles in the case of an ice front floating on water, whereas Reference Hanson and HookeHanson and Hooke (2000) performed finite-element simulations of a similar situation. As a general trend, Reference Hanson and HookeHanson and Hooke (2000) obtained non-linear increases of the tensile stress σt with the depth z (depth within the ice, different from the depth of the crevasse, l). The crevasse depth l itself probably modifies this stress profile σt(z) in a complex way, although quantitative information on this point is not available. For all these reasons, it is impossible to propose a “generic” expression for the stress intensity factor KI (l) as was done before for a crevasse within a glacier. In what follows, I first consider a simplified case of the situation depicted in Figure 4. It illustrates how a positive feedback between the crevasse length and the stress intensity factor naturally leads to a finite-time singularity for the crevasse growth rate (and therefore for crevasse opening) in agreement with the expression (1) proposed by Reference RöthlisbergerRöthlisberger (1977). Then, I discuss briefly how the finite thickness of the glacier or a more complex stress profile σt(z) can strengthen the feedback loop and consequently account for a variability of the exponent m in Equation (1).

Fig. 4. Surface crevasse near a glacier terminus: geometry and notation of the plane problem considered.
In a first step, the following crude approximations are made:
-
(i) the effect of the finite thickness of the glacier is neglected, i.e. H → +∞
-
(ii) the stress profile is considered to be constant, σt(z) = σt
-
(iii) the evolution of the stress profile as the crevasse deepens is neglected.
With these simplifying hypotheses, the stress intensity factor KI reduces to the first term of Equation (3), i.e.
The combination of Equations (2) and (4) gives:

that can be integrated analytically:

As n > 2, l follows a singular behaviour (l → +∞) at a critical time t c given by:

Contrary to the situation described in the previous subsection, the absence of overburden stress suppresses the inflexion point on the crevasse depth evolution. This evolution is characterized by a simple positive feedback loop: as the crevasse grows, the stress intensity factor increases (Equation (4)), which in turn increases the growth rate (Equation (2)), and so on up to infinity at t c. Obviously, the LEFM critical condition KI = KIC which initiates dynamic fracture will be reached a short time before t c. In terms of growth rate dl/dt, or equivalently of crevasse-opening rate at the surface (in fracture mechanics, crack length and opening are theoretically proportional), this finite-time singularity is expressed as:

This is the form of the equation proposed by Reference RöthlisbergerRöthlisberger (1977, equation (1)) to describe the acceleration of surface velocity across a crevasse before breaking off, with m = n/(n – 2). This suggests that subcritical crevassing is a possible explanation for the acceleration of crevasse growth before breaking of a glacier terminus.
The exponent m deduced from the crude hypotheses detailed above is close to (as n is large) and always larger than 1, whereas the data reported by Reference FlotronFlotron (1977) (see also Reference IkenIken, 1977) are best fitted by Equation (1) with m around 0.7. However, more recent measurements performed on a glacier terminus by the Swiss Federal Institute of Technology (ETH), Zürich (personal communication from Reference Pralong, Funk and LüthiM. Funk, 2003), indicate a variability of m, generally within the range 0.5–1.
The situation described above, which is given to illustrate the link between a positive feedback mechanism and the finite-time singularity of Equation (1), is obviously oversimplified. Similar calculations, not described here, of the crevasse evolution based on the integration of the crack-growth rate (Equation (2)) for more sophisticated situations led to the following qualitative conclusions:
-
(i) The effect of the glacier thickness introduces an additional positive feedback effect: KI (l) increases nonlinearly with l/H (Reference Van der VeenVan der Veen, 1998b). This results in a larger growth rate for a given crevasse depth, and therefore to a shorter failure time t c. In addition, the apparent exponent m (the slope of log(dl/dt) vs log [1/t c – t)]) slightly decreases approaching t c. However, this effect of the glacier thickness on m is significant only a short time before breaking.
-
(ii) A variability of the exponent m and/or its fluctuation during the crevasse life can also be explained by a tensile stress σt(z) varying with z, or by an evolution of the stress profile as the crevasse deepens. As a general rule, any mechanism which strengthens the positive feedback loop, such as a finite ice thickness (see point (i) above), an increase of σt(z) with depth or a strengthening of this increase as the crevasse deepens, tends to decrease m towards a lower bound of 1.
-
(iii) For all the situations, necessarily simplified, explored for this work, an exponent generally larger than and close to 1 was found. This disagreement with the scarce available field measurements (m in the range 0.5–1; see above) may have different origins such as more complex loading situations, or a non-linear scaling between the horizontal displacements measured on the glacier surface and the crevasse depth.
This dependence of crevasse-growth kinetics on either the stress profile or the glacier thickness illustrates the difficulty of predicting accurately the breaking-off time of an ice wall from an extrapolation of field velocity data.
Discussion and Conclusion
So far, no experimental data or field measurements are available on subcritical crack growth or subcritical crevassing in ice. However, the conditions encountered on glaciers such as visco-plastic flow, high homologous temperatures or the presence of chemical impurities are favourable factors for subcritical crevassing. In this paper, the behaviour of individual surface crevasses subjected to subcritical growth (Equation (2)) has been explored for two simplified loading situations. This mechanism makes it possible to interpret different observations on crevassing, icefalls and iceberg calving, that cannot be easily explained within a classical LEFM framework:
-
(i) Subcritical crevasse growth can explain the propagation of crevasses, under reasonable tensile stresses, from small microcracks nucleated by mechanisms at the crystal scale. Crevassing could start by the subcritical propagation of a fracture from a crystal-scale (few mm) flaw until a critical depth is reached where unstable dynamic propagation may occur.
-
(ii) Subcritical crevassing could explain the average propagation rates far below the body wave speeds observed by satellite imagery in ice shelves (see, e.g., Reference Fricker, Young, Allison and ColemanFricker and others, 2002). In the case of ice shelves, one may argue that these low speeds could result from an averaging over time of many step-like critical (KI ≥ KIC ) increments. However, this raises the problem of repeated crack arrests necessarily involving fast and large stress variations. A more realistic mechanism, specific to ice shelves, could be “cyclic fatigue” crack growth induced by tidal forcing (Reference Anandakrishnan and AlleyAnandakrishnan and Alley, 1997). Fatigue crack growth rate is generally described by a relation similar to Equation (2), the Paris law (see, e.g., Reference BroekBroek, 1982):

where N is the number of load cycles and ΔK = K max – K min is the amplitude of KI during the cycle. Note that K max is necessarily smaller than KIC , so fatigue crack growth is another kind of “subcritical” cracking. If loading frequency is constant through time, the crack-growth kinetics deduced from the integration of Equation (9) are strictly equivalent to those derived before, except that the exponents n reported for cyclic fatigue are generally lower than those reported for “static fatigue” (Equation (2); Reference BroekBroek, 1982). “Static fatigue” and “cyclic fatigue” effects can also positively interact in a mechanism called “corrosion fatigue”.
-
(iii) The positive feedback that results from subcritical cracking leads naturally to an acceleration of crevasse growth (and so of crevasse opening rate) before breaking off, in agreement with observations of glacier termini in temperate glaciers (Reference FlotronFlotron, 1977; Reference IkenIken, 1977). At much larger scale, a similar mechanism could explain the acceleration of fracture propagation within ice shelves during the last days preceding the calving of giant icebergs (Reference Fricker, Young, Allison and ColemanFricker and others, 2002), or even the acceleration of ice-shelf retreat at a regional scale (Reference Vaughan and DoakeVaughan and Doake, 1996). Note, however, that Reference Doake, Corr, Rott, Skvarca and YoungDoake and others (1998) proposed another explanation for this accelerating collapse, namely a large-scale structural effect.
If subcritical crevassing can rationalize different intriguing observations, this does not rule out the existence of other processes. In particular, any mechanism introducing a positive feedback necessarily leads to a finite-time singularity of the form of Equation (1). This is the case for damage accumulation discussed by Reference Pralong, Funk and LüthiPralong and others (2003). It is also possible to imagine a coupling between different mechanisms such as subcritical cracking and damage accumulation. Detailed analyses of field measurements may help in the future to discriminate different processes.
In conclusion, the analysis developed here calls for laboratory studies of subcritical cracking in ice as well as for additional field measurements of crevasse opening or icefall dynamics.
Acknowledgements
I would like to thank M. Funk for interesting discussions about glacier termini, as well as T. Jóhannesson (Scientific Editor), D. Vaughan and D. Cole whose reviews greatly helped to improve the clarity of the manuscript.