Introduction
In the fluid-dynamic modeling of sheet or channel flow, correspondence between the model and the full–scale process is assured if Reynolds and Froude numbers can be made equal in model and prototype. In order to do this exactly, a different fluid must be used in the model from that of the prototype in order to model kinematic viscosity correctly. However, this is generally not practicable, so the usual approach is to model the dominant scaling parameter, Froude number, and use analytical methodology to adjust for the lack of equivalence in Reynold’s number.
With regard to snow avalanche flow, in which modeling techniques would be beneficial, no analytical tool has been available to supplement the scaling laws to establish the rationale for modeling. Computer codes which have been reported recently, designated AVALNCH (Reference Lang, Lang, Dawson and MartinelliLang and others, 1979) and SMAC (Reference Pedersen, Pedersen, Dent and LangPedersen and others, 1979), provide analytical means for the establishment of criteria for avalanche modeling. Of particular interest is the construction of criteria to model the forces and pressures of avalanche impact upon structures and obstacles.
Computer program variables
In the computer programs two basic variables define the flow of snow. One is the kinematic viscosity v which is related to internal–energy dissipation. The second is the friction coefficient f which defines the surface slip velocity Us as a fraction of the main stream flow U 0. The explicit relationship is
In addition, we define terminal flow as the steady value attained by the mainstream velocity based upon slope angle, depth of flow, and specific values of v and f. Terminal velocity has been computed by Reference Lang, Lang, Dawson and MartinelliLang and others (1978) using program AVALNCH over a limited range of parameters.
The following relationship can be established for shear stress T 0 at the base of the flow by using Equation (1) to define velocity gradient and selecting the Newtonian viscosity law for shear stress in fluid:

In Equation (2) ρ is the material density and ![]() is the vertical dimension of the finite–difference grid used in the numerical representation of the flow in the computer program (Reference Dent and LangLang and Brown, 1980).
is the vertical dimension of the finite–difference grid used in the numerical representation of the flow in the computer program (Reference Dent and LangLang and Brown, 1980).
Experimental and computer-modeling criteria
To develop a composite evaluation of snow–avalanche modeling, we draw upon data from published sources in addition to test data we have obtained. To standardize the evaluation we select a slope angle of 45 °, which is common to several geometries used in published results.
One comparison which establishes the accuracy of the computer codes to model snow impact has been reported by Reference Pedersen, Pedersen, Dent and LangPedersen and others (1979) and is made possible by original experimentation of Reference SalmSalm (1964). One-meter-deep blocks of high-density snow (570 kg⁄m3) were slid down a 45° ramp and impacted at 12 m⁄s against a force–measuring target. Average normal stress measured was 165 kN–m2. In approximating this three-dimensional impact by a two-dimensional approximation using program SMAC, Reference Pedersen, Pedersen, Dent and LangPedersen and others (1979) report an average stress of 200 kN⁄m2. The difference is 21% too high, but this is consistent with the added dimensional constraint imposed on the computed result.
We establish the following specifications as representative of a nominal prototype avalanche associated with dry snow–pack conditions. If flow depth is taken as 1.0 m, then with kinematic viscosity v = 0.5 m2⁄s and surface friction coefficient f = 0.5, terminal velocity on a 45° slope is approximately 30 m⁄s. For this range of parameters, average normal stress of impact is reported by Reference SchaererSchaerer (1973) as being on the order of 200 kN⁄m2 from tests at Rodgers Pass, Canada, and 240 kN⁄m2 reported by Reference Dent and LangLang and Brown (1980) using program AVALNCH. Reynold number (Re) p and Froude number (Fr) p for this prototype configuration are

A series of tests were conducted in which sifted snow of density ρ = 360 kg⁄m3 was released onto a track 2.5 m long, 0.3 m wide, and with 0.05 m high side walls. The snow volumes released were 0.50 m in length, 0.30 m wide, and of depths h = 0.03, 0.05, and 0.07 m. The track surface consisted of glued sand of 1.0 mm grain diameter to simulate snow of the same mean diameter as that released. The tests were conducted in an upright freezer at — 10°C and the slope angle of the track was variable. Markings along the track provided means of estimating flow speed from 16 mm filming of each test (Fig. 1). A target having a frontal area 0.30 m wide and 0.05 m high was placed at the terminal end of the track. This rigid target was constructed from balsa wood and styrofoam weighing 0.024 kg, so that inertial effects of the target were minimized (Fig. 2). Two cantilever plates fitted with strain gages were calibrated to measure total force on the target.
With the track set at 45° slope, terminal velocity was found to be 3.7 m⁄s and the flow depth h was 0.011 m, independent of the depth of the snow in the released volume. Computer modeling of the flow using program AVALNCH required v = 0.017 m2⁄s and f = 0.017 (Figure 1)for duplication of the velocity along the path. With these parameter values, Reynolds and Froude number ((Re)m and (Fr) m) were computed to be 12.2 and 11.2 respectively.

Fig. 1. Track and target configuration.

Fig. 2. Target for snow–impact tests.
The ratio of Froude numbers (Fr) p /(Fr) m = 0.86 is close to unity, so that a scaling law based upon equivalence of Froude number is considered further.
(a) Geometric scaling

which sets the scale factor for subsequent calculations. h p and h m are the prototype and model flow depths respectively.
(b) Kinematic scaling

compared to an exact value ![]() .
.
(c) Normal–stress scaling

compared to the exact ![]() (12.9% difference) where we assume ρp=ρm
(12.9% difference) where we assume ρp=ρm
(d) Surface shear–stress scaling

compared to the exact (ρp⁄ρm) L r = 90.9 (15.1% difference).
(e) Reynolds number scaling

compared to the exact value of unity (a factor of 19.7 different).
(f) Kinematic–viscosity scaling

compared to the exact Lr3⁄2= 867 (a factor of 26.0 different).
From (e) and (f) we see that the scaling of viscosity is in error by a factor of 26.0, which is comparable to the Reynolds number mismatch. The non–modeling of kinematic viscosity also affects the lower surface shear stress (d); however, dominant correction of this must be attributed to the ratio of the friction factors. Thus, geometric, kinematical, and force or stress parameters closely approximate the scaling laws based upon equivalence of Froude number between prototype and model. Parameters involving kinematic viscosity which pertains to internal circulation and internal–energy dissipation tend not to scale correctly, unless internal adjustment occurs.
Computer and experimental impact correspondence
Experimentally, total force on the target was recorded by output of the four–active–arm strain–gage bridge displayed on a storage oscilloscope, and the trace photographed. A total of four tests in which depth of released snow was varied were run with the track set at 45° slope. Traces of the four tests are shown in Figure 3a, showing the scatter, particularly that of the transient phase of each impact. However, by the time the snow had flowed to the target, depth of flow averaged 0.011 m in all tests, and the flow velocity was 3.7 m⁄s. The force trace of each test was different because of differences in leading–edge slope and different distributions of small blocks of snow that had not disintegrated during the flow. Thus, a composite force profile which is an average of the four tests can be constructed, and is shown in Figure 4.
In the computer, program AVALNCH was used to estimate the internal viscosity and the surface friction coefficient in order to duplicate the velocity distribution of the flow. These values were then used in program SMAC to represent the impact and material overflow of the target. In the computer simulation the target was represented as a rigid barrier, so that force transient response differs from the experimental profile. However, average force response between computer and experimental results agree well, as seen in Figure 4. Average force during the time period between 100 ms and 250 ms is 11.0 N experimentally, and 9.8 N (Fig.3 and Fig.4. ) in the simulation, which is an 11% difference. In comparing the average or steady forces on the impact barrier, effects of material compressibility are clearly unimportant. During steady flow a triangular wedge has already formed at the barrier and flow is established over the wedge. If compressibility enters into consideration, it would be during formation of the wedge which is during the transient phase of the force profile.

Fig. 3. Force traces of impacts. a. 45° slope. b. 53.5° slope.
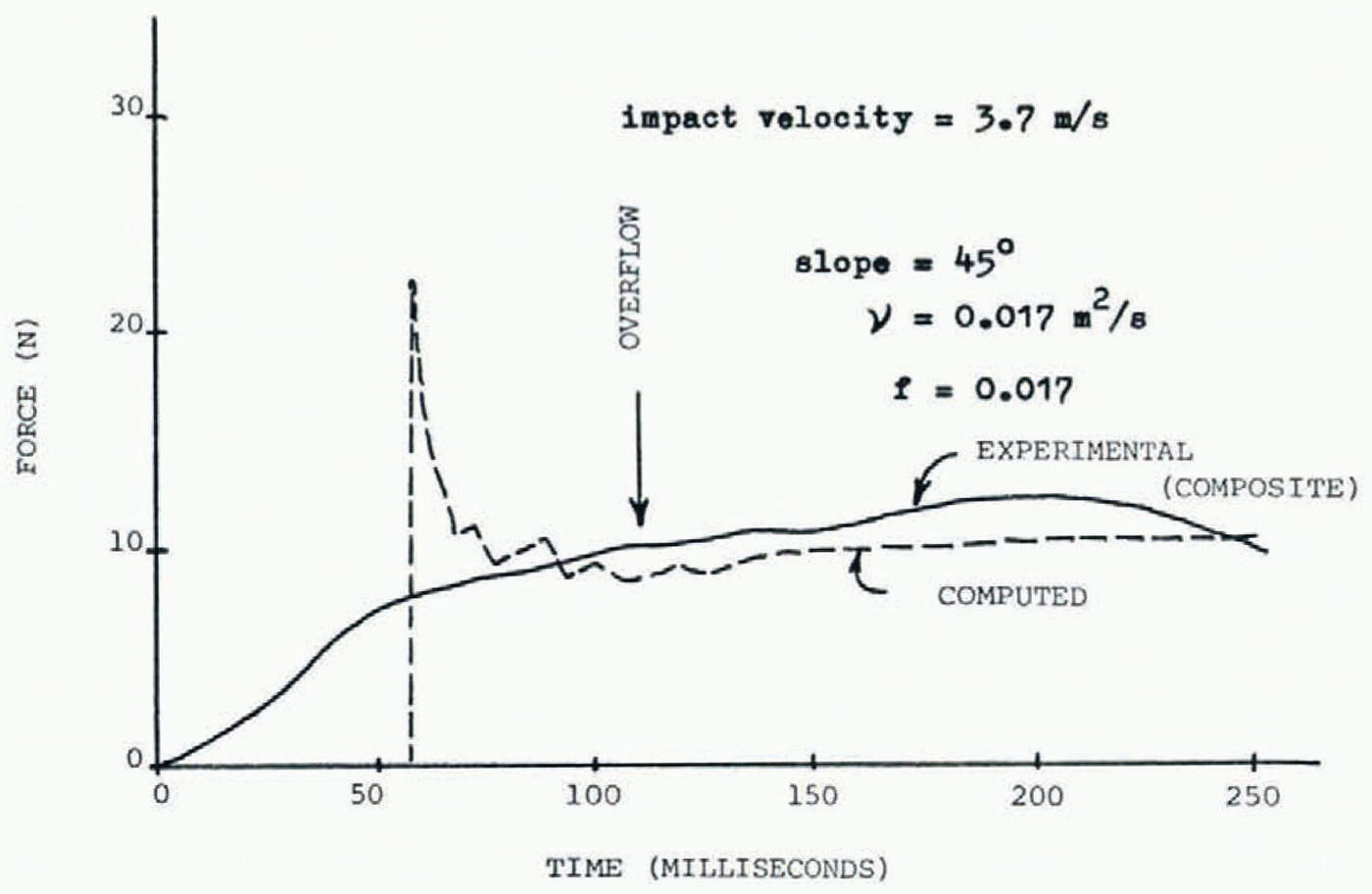
Fig. 4. Average experimental and computed normal force profiles of snow impact on a 45° slope.
Using the same experimental procedure as already described, five tests were run with the track set at 53.5° slope (Fig. 3b). Flow depth was, on average, 0.011 m and the terminal velocity was 4.8 m⁄s. Computed and measured forces on the target are shown in Figure 5. Average experimental force was 14.5 N, and the average computed force was 15.5 N (6.9% difference). For these results viscosity v = 0.015 m2/s and friction coefficient f = 0.015.
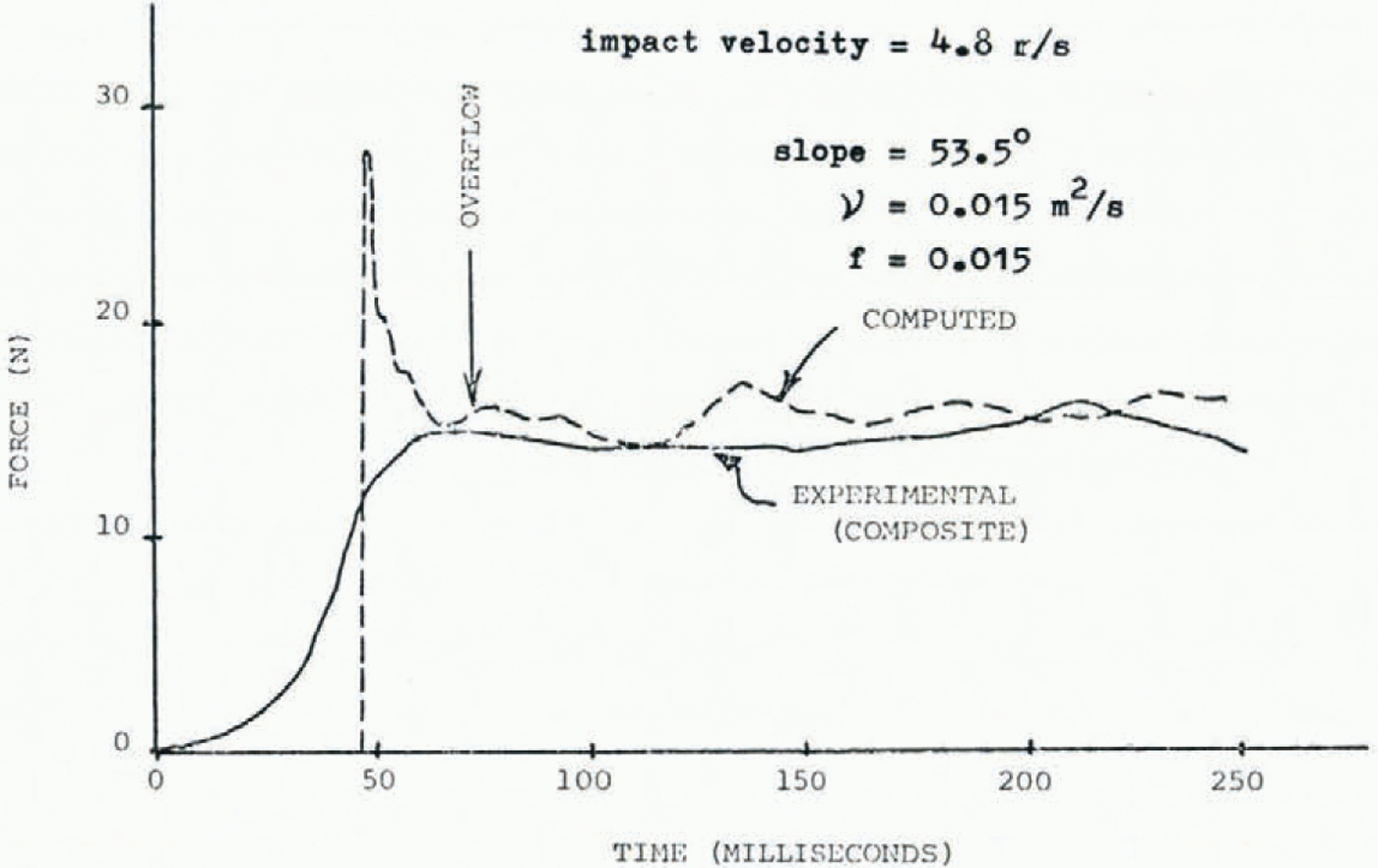
Fig. 5. Average experimental and computed normal force profiles of snow impact on a 53.5° slope.
On the basis of a number of flow and impact tests described here, we have developed a graph showing the relationship between avalanche flow depth and kinematic viscosity (Fig. 6). For deep flows, kinematic viscosity is asymptotic to a value of 0.5 m2⁄s and falls to lower values for shallower flow depths. For v = 0.5 m2⁄s the snow is nominally dry midwinter hard–pack. Values of v as low as 0.35 m2⁄s have been used for soft snow avalanches, and values greater than 0.5 m2⁄s have been used with wet–snow cases. Numerical experimentation on a number of avalanche configurations has shown that in setting v = f, numerically, satisfactory results have been obtained. The impact results given here are based upon the numerical equivalence of viscosity and friction.
We note that the use of parameters f and v, as specified here, correspond to snow–flow modeling by computer program AVALNCH. Recent refinements in snow–flow modeling have resulted in use of other fluid mechanisms such as reported by Reference Dent and LangDent and Lang (1980). In the present application, use of f and v to maintain the velocity of flow at impact has proved satisfactory.

Fig. 6. Kinematic viscosity of flowing snow as a function of flow depth using program AVALNCH.
Conclusions
Small–scale modeling of snow avalanches is shown to be feasible for geometric, kinematic, and force and stress variables based upon numerical equivalence of the Froude number between prototype and model. Fluid for the model flow is sifted snow with density of the same order as that of the prototype. Use of sifted snow violates the model laws for scaling of viscous properties and, hence, also of Reynold’s number. Viscosity affects primarily internal- energy dissipation due to internal circulation in the flow, which has negligible influence on the force and dimension variables relating to impact. For flow modeling the error in viscosity scaling is offset by the scaling of the surface friction coefficient. Computer programs AVALNCH and SMAC accurately predict model response by the correct scaling of viscosity and friction, as is determined by comparison with corresponding experimental results. Thus, these computer programs provide analytical methods for continued work in model and prototype studies of avalanche–flow and impact processes.
Acknowledgements
The authors wish to express their thanks for support of this work to Dr M. Martinelli, Jr, group leader for snow research at the Rocky Mountain Forest and Range Experiment Station, Fort Collins, Colorado (Agreement No. 16-884-GA) and Professor Theodore Williams, Department Head of Civil Engineering and Engineering Mechanics, Montana State University, Bozeman, Montana.







