List of Symbols
List of Symbols

1. Introduction
The most significant cause of future sea-level rise is likely to be enhanced discharge through outlet glaciers and ice streams that are ‘lubricated’ by subglacial meltwater (Reference SolomonSolomon and others, 2007). The distribution of water pressure at the glacier bed controls the effective stress N, which is expected to influence the basal shear resistance τ
b to glacier sliding and till deformation (e.g. Reference PatersonPaterson, 1994). However, the sliding law that describes how τ
b, the sliding rate W
s and N are related has remained elusive. The predictive abilities of models for glacier and ice-sheet flow are limited by this deficiency in our understanding of the basal boundary conditions (Reference Fountain and WalderFountain and Walder, 1998; Reference MarshallMarshall, 2005). The work described here examines the controls that seepage flows exert on the average effective stress ![]() beneath soft-bedded glaciers.
beneath soft-bedded glaciers.
The morphology of subglacial drainage is thought to play a key role in the dynamics of glacier flow (e.g. Reference WeertmanWeertman, 1972; Reference KambKamb, 1987). For example, observations (Reference Harper, Humphrey, Pfeffer and LazarHarper and others, 2007; Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008) and theory (Reference LliboutryLliboutry, 1968; Reference FowlerFowler, 1987; Reference SchoofSchoof, 2005) suggest that changes in the water volume stored in cavities beneath hard-bedded glaciers alter the surface area over which significant shear resistance is imparted to the glacier base. Similar behavior may also occur beneath soft-bedded glaciers, particularly when the bed itself is deformed by the overriding glacier flow (e.g. Reference SchoofSchoof, 2007). While connections between basal water supply and glacier motion have long been recognized, several recent developments have drawn further attention to the dynamic nature of subglacial processes. These include reported correlations between summer surface melting and accelerated flow near the margins of the Greenland ice sheet (Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002; Reference Price, Payne, Catania and NeumannPrice and others, 2008), recent satellite observations of lake drainage events beneath West Antarctica (Reference Fricker, Scambos, Bindschadler and PadmanFricker and others, 2007), global positioning system (GPS) measurements of short-term flow variations in ice-stream regions (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003) and the intriguing discovery of glacial earthquakes with surface-wave magnitudes of 5 and larger in Greenland and Alaska (Reference Ekström, Nettles and AbersEkström and others, 2003).
Subglacial drainage systems are dominated by channelized flows that efficiently transport water over long distances (e.g. Reference RöthlisbergerRöthlisberger, 1972; Reference WeertmanWeertman, 1972; Reference NyeNye, 1976; Reference ShoemakerShoemaker, 1986; Reference Walder and FowlerWalder and Fowler, 1994; Reference NgNg, 1998; Reference ClarkeClarke, 2005). Beneath soft-bedded glaciers with relatively flat beds, water transport between major subglacial conduits and most of the basal surface area is expected to occur through seepage flows. The hydraulic gradients needed to drive this local transport imply effective stress variations that can be integrated to evaluate the average effective stress ![]() for a given drainage configuration and heat-flow regime. The average basal shear stress is expected to depend on
for a given drainage configuration and heat-flow regime. The average basal shear stress is expected to depend on ![]() ; for example,
; for example, ![]() if till behaves as a Coulomb-plastic material with friction coefficient μ and negligible cohesion.
if till behaves as a Coulomb-plastic material with friction coefficient μ and negligible cohesion.
In addition to storing and transporting vast quantities of fresh water, glaciers are among the most powerful erosive agents on the planet (Reference Alley, Cuffey, Evenson, Strasser, Lawson and LarsonAlley and others, 1997). The current work is of relevance to the manner in which soft-bedded glaciers entrain sediments. The treatment has parallels with that described in an earlier study by Reference IversonIverson (2000). A series of laboratory experiments (Reference IversonIverson, 1993; Reference Iverson and SemmensIverson and Semmens, 1996) and field studies (Reference IversonIverson and others, 2007) provide convincing evidence for the ability of ice to regelate into porous sediments when the effective stress is high. Reference IversonIverson (2000) modified and extended the theory of Reference PhilipPhilip (1980) to predict the steady-state depth of ice penetration that enables a balance between the rates of melting and pressure-induced regelation. Since the predicted rate of regelation increases with effective stress, the thickness of the regelation layer, identified here as a fringe, is expected to increase towards major drainage conduits.
A significant uncertainty noted by Reference Alley, Cuffey, Evenson, Strasser, Lawson and LarsonAlley and others (1997) and Reference IversonIverson (2000) concerned the role of the ice–liquid surface energy in impeding ice infiltration through fine-grained till. The themodynamic and mechanical equilibrium conditions at the ice–liquid interface have recently been formulated to take these effects into account and determine a lower-bound p f on the effective stress required for ice to infiltrate a given sediment (Reference RempelRempel, 2008). For soft-bedded glaciers, a one-dimensional treatment of the vertical force, mass and heat balance at the glacier bed demonstrates links between the effective stress N, the rate of basal freeze-on V (or melting with V < 0), sliding speed W s and details of the near-bed temperature distribution and till properties. A major advance is the prediction for N > p f of the steady-state fringe thickness h during both net melting and net freezing at the glacier bed. For convenience, the assumption made here is that the fringe is attached to the glacier base and hence able to transport its sediment load with the glacier at sliding speed W s.
Many past field studies of subglacial hydrological networks have taken place on hard-bedded valley glaciers that experience substantial diurnal and seasonal variations in the flux of meltwater that reaches the bed (Reference Iken and BindschadlerIken and Bindschadler, 1986; Reference Stone and ClarkeStone and Clarke, 1993; Reference Fountain, Jacobel, Schlichting and JanssonFountain and others, 2005; Reference Lappegard, Kohler, Jackson and HagenLappegard and others, 2006; Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008). These glaciers often have much smaller or negligible melt inputs to the bed during winter months, and water storage at the bed is limited to the volumes contained in cavity systems downstream of bedrock obstacles. There have been a few important field studies of the fluid pressure distributions beneath ice sheets that are sufficiently cold and thick to be relatively unaffected by inputs of surface meltwater. They are generally expected to be underlain by hydrological networks that are not strongly affected by seasonal forcings (e.g. Reference Engelhardt and KambEngelhardt and Kamb, 1997). The modeling efforts described below are most directly applicable to relatively stable situations such as these, but model extensions can be made to investigate the dynamics in more transient environments. For example, an interesting intermediate case is suggested by extensive studies of the hydrological networks near the margins of Breiðamerkurjökul, Iceland (Reference Boulton, Lunn, Vidstrand and ZatsepinBoulton and others, 2007a,Reference Boulton, Lunn, Vidstrand and Zatsepinb). There, high geothermal heat input causes major melt conduits to persist over decadal-long observation periods, with hydrological networks augmented by a series of more ephemeral conduits that accommodate summer meltwater inputs.
This paper is organized as follows. First, a description is given of the conditions for thermodynamic and mechanical equilibrium at the glacier base, the transport of heat and fluid mass and the constitutive behavior of till. These considerations are then implemented to predict the major characteristics of hydrological networks that underlie an idealized glacier that is separated from impermeable bedrock by a layer of permeable till. The modeling is focused on cases of steady drainage where seepage flow through the till transports water between subglacial conduits and the glacier base. A broad range of potential steady-state behavior is examined using a simplified treatment that approximates the seepage flow by focusing on the depth-integrated horizontal transport. The effects of vertical fluid flow within the unfrozen till are not expected to alter the gross qualitative behavior, as demonstrated in the Appendix by comparisons between the depth-integrated treatment and a more complete treatment that accounts for these complications. The paper closes with a discussion of the implications of this work and directions for future research.
2. Model Formulation
The temperature and fluid pressure beneath warm-based, soft-bedded glaciers are determined by the local equilibrium conditions. The local heat balance determines whether water freezes onto or melts away from the glacier base. Mass-balance considerations necessitate lateral water transport through the unfrozen till to facilitate this phase change.
Basal equilibrium conditions
For liquid water and ice to coexist in equilibrium, the temperature must be close to the pressure-melting point T m(p). Lateral pressure gradients in the water immediately adjacent to the ice drive fluid transport when the local heat balance promotes net freezing or melting. Thermodynamic and mechanical equilibrium are assumed at the ice–liquid interface. Three different potential geometries for portions of the basal interface are shown schematically in Figure 1.

Fig. 1. Schematic diagrams of the region near a glacier base above water-saturated sediments. (a) A macroscopic conduit is present; the glacier base is at Tl = T m and the fluid pressure immediately adjacent to ice is p = σ n. (b) Sediment particles support part of the glacier weight; p < σ n and Tl < T m, but Tl still exceeds the level T f needed for ice to extend through pore throats of radius R p (i.e. K ≈ 2/R < 2/R p). (c) A partially frozen fringe of thickness h and ice saturation S i extends beneath the glacier base; at z = l, Tl < T f and the temperature rises to T f only at z = l − h, where the fluid pressure p < σ n − p f.
In Figure 1a, the till and ice are separated by a layer of water that is of a thickness (e.g. O(1 μm)) such that intermolecular forces between the till and ice are of negligible strength. There are many subglacial environments where such macroscopic water layers are present, including lakes, channels, water sheets and cavities. In this paper, the term ‘conduit’ is used to refer to any such region that may facilitate rapid liquid transport (Reference WeertmanWeertman, 1972). In Figure 1a, the ice–liquid interface is depicted as being flat for simplicity although, in practice, its geometry may be more complicated. Mechanical equilibrium requires that the liquid pressure p on the ice–water interface be equal to the normal stress σ n in the ice. As defined here, the effective stress N ≡ σ n − p = 0 in such regions. (A common alternative definition not used here refers to the effective stress as the difference between the ice pressure, that is the average of the principal components of the stress tensor, and the fluid pressure p. The definition of N given here is chosen to simplify the presentation of the vertical force balance and be consistent with the use of Terzaghi’s effective stress principle (Reference TerzaghiTerzaghi, 1943) in the description of frictional resistance below.) Thermodynamic equilibrium is achieved when the interface temperature Tl = T m(p).
In Figure 1b, the ice conforms to the upper surfaces of till particles from which it is separated by thin liquid films. Thermodynamic equilibrium requires that the temperature of the ice–liquid interface Tl < T m so that some of the glacier weight can be supported by interactions between the ice and the till particles across the liquid films (e.g. Reference ShreveShreve, 1984; Reference DashDash, 1989; Reference Dash, Fu and WettlauferDash and others, 1995, Reference Dash, Rempel and Wettlaufer2006; Reference WettlauferWettlaufer, 1999). Where the ice–liquid interface veers away from the particles, the Gibbs–Thomson effect describes how surface energy γ il prevents it from penetrating through the pore throats when Tl > T f . For pore throats of characteristic radius R p, T f = T m [1 − 2 γ il/( ρ i LR p)] where ρ i is the ice density and L is the latent heat of fusion. For physical intuition, T m − T f ≈ 0.006°C when R p = 10 μm. The pore geometry is difficult to quantify directly, but T f can be inferred from measurements of the water content of porous media at different sub-T m temperatures. For many different sediment types, the value of T f can be extracted from tables of data compiled by Reference Andersland and LadanyiAndersland and Ladanyi (2004). In the pores immediately beneath the ice, mechanical equilibrium requires that (Reference RempelRempel, 2008)
where K < 2/R p is the curvature of the ice–liquid interface in the pore throats and δp is the difference in fluid pressure between the pores and the films that separate the ice from the particles. Because rates of melting and freezing are typically quite low (i.e. <100 mm a−1), δp can be considered negligible everywhere except where water must flow long distances through films around larger clasts and boulders.
The strengths of ice–till interactions increase as the temperature cools and the liquid films get thinner. For this reason, if N increases at the ice base, Tl must decrease to enable ice–till interactions to support an increased load. As Equation (2) indicates, this causes the curvature of the ice–liquid interface to increase. Ice first penetrates through the pore throats once K = 2/R p so that Tl = T f and N ≈ p f = ρ i L(T m − T f)/T m. Because the presence of ice in the pores reduces the permeability, the pressure p f is an important natural scale for effective stress variations associated with seepage transport under soft-bedded glaciers. For the example given above with T m − T f = 0.006°C, p f ≈ 7 kPa. Larger values of p f are expected for sediments that are characterized by smaller pore apertures (e.g. Reference Andersland and LadanyiAndersland and Ladanyi, 2004; Reference RempelRempel, 2008).
In Figure 1c, the ice extends downwards into the till to form a fringe of thickness h and porosity ϕ, with a partial ice saturation S i that decreases with temperature (e.g. Reference Cahn, Dash and FuCahn and others, 1992). The temperature at the base of the fringe is T f , whereas the temperature at z = l where the ice first encounters till is Tl < T f . For this case, mechanical equilibrium requires that at z = l − h (Reference RempelRempel, 2008)
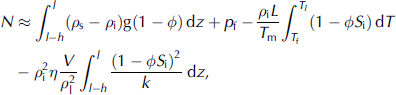
where ρ s and ρ l are the densities of the soil particles and liquid water, g is the acceleration due to gravity, η is the viscosity of water, V is the rate of freezing (V < 0 for melting) and k is the ice-saturation-dependent permeability to fluid flow. The first term on the right-hand side of Equation (2) accounts for the weight of till within the fringe. The next two terms are the net vertical force per unit area produced by intermolecular interactions between the ice and till. The final term accounts for the deviation of the fluid pressure from hydrostatic conditions that is required to move water vertically through the fringe. Derivations of Equations (1) and (2) and further discussion of minor correction terms that are neglected here are given in Reference RempelRempel (2008). A similar relationship to Equation (2) can be extracted from field-tested models of frost heave (e.g. Reference O’Neill and MillerO’Neill and Miller, 1985; Reference NixonNixon, 1991; Reference Fowler and KrantzFowler and Krantz, 1994) that have recently been updated within the context of a contemporary understanding of pre-melting behavior (e.g. Reference Dash, Fu and WettlauferDash and others, 1995, Reference Dash, Rempel and Wettlaufer2006; Reference Rempel, Wettlaufer and WorsterRempel and others, 2001, Reference Rempel, Wettlaufer and Worster2004; Reference RempelRempel, 2007).
Heat balance
The flow of heat into the glacier base at z = l controls the rate of freezing or melting. The latent heat consumed during freezing is balanced by the heat transport into and away from the interface so that the freezing rate is
In Equation (3), Q b is the heat flux into the glacier base, Q g is the geothermal heat flux, Q f is the rate of work performed at the basal interface and
is the ice content of the fringe. Spatial and temporal changes in Q b are controlled by the rate of mechanical dissipation in the ice in addition to advective and diffusive heat transport through the ice. Q g is expected to be nearly constant over relatively large distances and long timescales. For ice that slides over till at velocity W s, the rate of mechanical dissipation at the sliding interface Q f = τ b Ws can vary over short distances because of heterogeneities in τ b. The final term in Equation (3) accounts for changes in the ice content of the fringe (if present). For physical intuition, the steady freezing rate predicted by Equation (3) is approximately 0.1[Q b − (Q g + Q f ) (mm a−1 mW−1 m2) so that for a temperate glacier with Q b ≈ 0, V ≈ −6 m ma−1 when Q g + Q f ≈ 60 mW m−2.
Water transport
Water flows to or from the glacier base to facilitate the melting or freezing required by the heat balance. Transport is driven by gradients in the fluid potential, and the volume flux along each pathway depends on the resistance to flow produced by interactions with solid surfaces. For a given potential drop, flow through large conduits is most efficient and is expected to transport the greatest fluid volumes (e.g. Reference RöthlisbergerRöthlisberger, 1972; Reference Walder and FowlerWalder and Fowler, 1994; Reference Fountain and WalderFountain and Walder, 1998).
When most of the basal cross-sectional area of a soft-bedded glacier is adjacent to water-saturated till, fluid transfers with conduits are accommodated by seepage flows that move water according to Darcy’s law at transport rate
where k 0 is the permeability of the unfrozen sediment. The hypothesis explored here is that the requirements for seepage transport can exert a dominant control on the average effective stress at the glacier base.
The fluid pressure p = σ n − N, where N satisfies the local basal equilibrium considerations outlined above. If the layer of unfrozen sediment is thin in comparison to the scale of horizontal transport then the rate of vertical fluid motion is small enough that the vertical fluid pressure gradient is approximately hydrostatic and the seepage transport rate can be written:
In Equation (5), ∇ xy is the horizontal gradient operator and σT is defined as the amount by which bridging stresses cause σ n to exceed the glacier weight per unit area. Minor terms involving the density difference between water and ice are neglected.
The seepage flow satisfies a mass conservation condition so that within the water-saturated till,
Equation (6) can be vertically integrated over the thickness of a till layer with its base at z = b to find that changes in the horizontal seepage flow rate are governed by
To arrive at Equation (7), the till layer has been assumed to rest upon an impermeable substrate and freezing at the top of the till layer is treated as a sink on the horizontal transport.
Weertman (Reference Weertman1972) showed that beneath hard-bedded glaciers the requirements of creep closure can cause the normal stress distribution near the boundaries of Röthlisberger channels to prevent water exchange with the rest of the glacier base. This is consistent with the predictions of Equation (5) when ∇ xy (σT − N) changes sign as a conduit is approached from outside. Walder and Fowler (Reference Walder and Fowler1994) argued that water supply to ‘canals’ cut into soft sediments would not be impeded to the same extent as for conduits on top of impermeable substrates. Ng (Reference Ng1998, Reference Ng2000) calculated the normal stress distribution at the ice–till interface outside an idealized canal with a width that greatly exceeds its depth. It was found that |σT | is negligible at distances much larger than the canal width, but increases abruptly to become undefined at the conduit boundary. Regularization of this result probably requires a more detailed analysis that incorporates additional physical interactions within the thin boundary layer where |σT | becomes significant (Ng, Reference Ng2000). This difficult problem is not considered further here; ∇σT is in fact neglected in the calculations that follow. Instead, the simplifying assumption is that water is transported across a boundary layer near the conduit wall, and a specified effective stress N C is applied as a boundary condition on the till side of the conduit.
The behavior of ice in till
Certain properties of the till are important for determining the behavior of the subglacial system. Tests on a range of unconsolidated materials suggest that the dependence of ice saturation on temperature is well represented by an empirical relationship of the form (Andersland and Ladanyi, 2003; Rempel, Reference Rempel2007, Reference Rempel2008)
where T < T f and the exponent β is typically less than unity. The permeability in the fringe is modeled using an empirical relationship of the form (Nixon, Reference Nixon1991; Andersland and Ladanyi, Reference Andersland and Ladanyi2004)
where the exponent α is typically greater than unity and k 0 is the permeability of water-saturated (i.e. ice-free) till.
For the calculations presented here, Equations (8) and (9) are evaluated using parameters reported for Chena silt, a fine-grained sediment that has been well characterized in terms of its ice-saturation behavior and permeability variations with sub-zero temperatures (Andersland and Ladanyi, Reference Andersland and Ladanyi2004). Good correlations between empirical ice-saturation parameters β and T f from Equation (8) and the measured specific surface areas SSA of many different silts and clays suggest that (SSA) might be used to estimate T f and hence p f for different subglacial sediments (Rempel, Reference Rempel2008). Notably, the SSA of Chena silt is within the range reported for sediments recovered from the base of Kamb Ice Stream, West Antarctica (Christoffersen and Tulaczyk, Reference Christoffersen and Tulaczyk2003). It can be argued that most tills are likely to be more poorly sorted than those derived from marine sediments near the Siple Coast. Nevertheless, the onset of ice infiltration that defines the pressure scale p f is expected to be controlled primarily by the most fine-grained fraction of heterogeneous particle mixtures. Clearly, glaciers are underlain by a rich variety of sediments and the soil parameters used here are only meant to illustrate the types of behaviors that are expected. Direct measurements of variations in S i and permeability with temperature are needed for specific field settings.
3. Steady Hydrological Networks
Figure 2 shows a schematic view of the drainage system beneath a soft-bedded glacier that is flowing in the ![]() direction. Variations in H, l and b are also assumed to occur only in the
direction. Variations in H, l and b are also assumed to occur only in the ![]() direction. Under these simplified conditions, when downstream variations in σT
are small, the maximum hydraulic gradient and hence the subglacial conduits are expected to be aligned with the surface slope. For a given conduit spacing 2D, the model framework described above can be used to predict the average effective stress that persists over the glacier bed. When the sliding velocity W
s = 0 and there is a uniform rate of basal melting, the results below agree with those given previously by Shoemaker (Reference Shoemaker1986) who provides an interesting analysis of the connections between subglacial drainage and the near-terminus profiles of idealized ice sheets.
direction. Under these simplified conditions, when downstream variations in σT
are small, the maximum hydraulic gradient and hence the subglacial conduits are expected to be aligned with the surface slope. For a given conduit spacing 2D, the model framework described above can be used to predict the average effective stress that persists over the glacier bed. When the sliding velocity W
s = 0 and there is a uniform rate of basal melting, the results below agree with those given previously by Shoemaker (Reference Shoemaker1986) who provides an interesting analysis of the connections between subglacial drainage and the near-terminus profiles of idealized ice sheets.

Fig. 2. Schematic diagram of a glacier that sits upon a layer of till cut by subglacial conduits.
Cross-sections through two potential steady-state hydrological networks are shown schematically in Figure 3. These can be thought of as close-ups of part of the lower portion of Figure 2 under different heat-flow regimes. In Figure 3a, the basal heat flux Q b is insufficient to remove the combination of geothermal (Q g) and dissipative (Q f ) heat, so V < 0 and net melting occurs at the glacier base according to Equation (3). A seepage flow transports meltwater to the conduit, and the effective stress distribution required to drive this flow has N decreasing towards the drainage divide.

Fig. 3. Possible hydrological networks: (a) net melting takes place at the glacier base and (b) net freezing takes place and ice is accreted to the glacier base.
In Figure 3b, the basal heat flux Q b exceeds the sum of Q g and Q f so V > 0. Equation (3) describes the rate with which net freezing takes place at the glacier base. As shown, mass balance is satisfied by flow through a conduit on the left that supplies the seepage flow tapped by the freeze-on process. The decrease in fluid pressure needed to drive this flow increases the effective stress N towards the drainage divide at larger x. If the seepage flow path is sufficiently long that N > p f far from the supply conduit, a fringe with partial ice saturation will form (as indicated on the right).
No fringe present: h = 0
The controls on average effective stress are illuminated by examining simple cases in which ∇σ T → 0. With the fringe absent, h = 0 and Equation (5) becomes
where ![]() and
and ![]() are unit vectors. Seepage flows have components in both the direction of glacier flow and in the cross-flow direction. The total seepage flux in the down-glacier
are unit vectors. Seepage flows have components in both the direction of glacier flow and in the cross-flow direction. The total seepage flux in the down-glacier ![]() direction is assumed to be relatively constant in comparison with that of the cross–glacier
direction is assumed to be relatively constant in comparison with that of the cross–glacier ![]() direction. This is expected to be the case when variations in till thickness l − b and surface slope α in the direction of glacier flow occur over a length scale that is much longer than the distance D from a conduit to the drainage divide.
direction. This is expected to be the case when variations in till thickness l − b and surface slope α in the direction of glacier flow occur over a length scale that is much longer than the distance D from a conduit to the drainage divide.
Experiments suggest that till can often be approximated as a Coulomb-plastic material (e.g. Terzaghi, Reference Terzaghi1943), with the local shear resistance satisfying τ b ≈ μN for a constant friction coefficient μ (Kamb, Reference Kamb1970; Clarke, Reference Clarke1987; Reference Iverson, Hooyer and BakerIverson and others, 1998; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000; Fowler, Reference Fowler2003). For sliding rate W s, substituting Q f = μNW s into Equation (3) and defining the length scale
the pressure scale
and the velocity scale
Equation (10) combines with the steady-state mass-balance condition from Equation (8) to give
Equation (11) describes how the effective stress changes over a characteristic distance d . For example with N(0) = N C, N(D) = N D and dN/dx = 0 at x = D, the profile satisfies
where W s > 0. When Q g > Q b and melting takes place, the mass balance requires that N C >N D. However, N C < N D < |NQ |W 0/W s when Q b > Q g and freezing occurs. The upper limit on the effective stress at the drainage divide N D < |NQ |W 0/W s during freezing arises because higher values of N generate enough frictional dissipation to cause net melting. Profiles of the effective stress distribution for this and other cases are shown in Figure 4, and their mathematical descriptions are summarized in Table 1 and in the Appendix.

Fig. 4. Profiles of (a) scaled effective stress N/p f and (b) scaled fringe thickness h/(l − b) when D = 2(l − b), Q g = 60 mW m−2 and for the values of Q b given in the legend.
Table 1. Equations describing the steady-state behavior with N(x = 0) = N C and N(x = D) = N D

Of more importance to the overall glacier behavior than the local value of N(x) is the average effective stress over the glacier base:
Importantly, ![]() and by extension the average basal shear stress
and by extension the average basal shear stress ![]() is sensitive to the glacier sliding rate even when the till behaves locally as a Coulomb-plastic material. The sensitivity of
is sensitive to the glacier sliding rate even when the till behaves locally as a Coulomb-plastic material. The sensitivity of ![]() to W
s is greatest when Q
b and Q
g are similar in magnitude and the conduit spacing is large. For example, during freezing with N
D approaching |NQ
|W
0/W
s, D ≫ d and Equation (13) predicts that
to W
s is greatest when Q
b and Q
g are similar in magnitude and the conduit spacing is large. For example, during freezing with N
D approaching |NQ
|W
0/W
s, D ≫ d and Equation (13) predicts that ![]() , as noted in Table 1 (section A). Such ‘rate-weakening’ behavior suggests the potential for instability, as discussed below in section 4.
, as noted in Table 1 (section A). Such ‘rate-weakening’ behavior suggests the potential for instability, as discussed below in section 4.
In the special case where the dissipative heat flux Q f = 0, for example when W s = 0 and the glacier does not slide, the average effective stress between the conduit and the divide is (for details see Table 1, section B)
Since N
D > N
C when freezing takes place at the glacier base, whereas N
C > N
D during melting, Equation (14) predicts that for the same overall magnitude of effective stress difference |N
C
N
D|, ![]() is higher during freezing than during melting. The argument that
is higher during freezing than during melting. The argument that ![]() is greater during freezing than melting has been made before based on the dependence of void ratio on effective stress. Here, even though changes in void ratio have not been accounted for,
is greater during freezing than melting has been made before based on the dependence of void ratio on effective stress. Here, even though changes in void ratio have not been accounted for, ![]() is still shown to be higher during freezing than melting because of the distribution of N(x) required to drive the seepage transport. The N/p
f profile for Q
b = 30 mW m−2 and the lower of the two profiles with Q
b = 90 mW m−2 in Figure 4a provide examples where N ranges between similar but opposite values at the conduit and divide. However, it is clear that
is still shown to be higher during freezing than melting because of the distribution of N(x) required to drive the seepage transport. The N/p
f profile for Q
b = 30 mW m−2 and the lower of the two profiles with Q
b = 90 mW m−2 in Figure 4a provide examples where N ranges between similar but opposite values at the conduit and divide. However, it is clear that ![]() is higher for the freezing case (e.g. Q
b = 90mWm−2 > Q
g).
is higher for the freezing case (e.g. Q
b = 90mWm−2 > Q
g).
Figure 5a and b show predicted values of ![]() and D/(l − b) respectively as a function of Q
b with Q
g = 60mWm−2 in the limiting cases where p
f > N > 0. Solid curves are for dissipative heating Q
f = μNW
s with μ = 0.6 and W
s = 10 m a−1. Nominal values for the other control parameters are summarized in Table 2. Dashed lines are for the special case when Q
f = 0. As long as Q
f ≪ |Q
g − Q
b|, the role of dissipation in producing additional melt is minor so the solid curves tend towards the dashed lines at large and small values of Q
b. As shown in Figure 5a,
and D/(l − b) respectively as a function of Q
b with Q
g = 60mWm−2 in the limiting cases where p
f > N > 0. Solid curves are for dissipative heating Q
f = μNW
s with μ = 0.6 and W
s = 10 m a−1. Nominal values for the other control parameters are summarized in Table 2. Dashed lines are for the special case when Q
f = 0. As long as Q
f ≪ |Q
g − Q
b|, the role of dissipation in producing additional melt is minor so the solid curves tend towards the dashed lines at large and small values of Q
b. As shown in Figure 5a, ![]() is twice as large during freezing with N
C = 0 and N
D = p
f as it is during melting with N
C = p
f and N
D = 0. When Q
g and Q
b are closely matched, dissipative heating exerts an important control on the quantity of liquid to be transported. With N
C = 0 during freezing, D increases rapidly as N
D approaches the limiting value |NQ
|W
0/W
s. Values of D/(l − b) plotted in Figure 5b are the largest possible, with p
f > N > 0 everywhere between the conduit and divide. When N > 0 everywhere, for larger D a fringe is expected to form; the fringe is located near the divide when freezing takes place and near the conduit when melting takes place.
is twice as large during freezing with N
C = 0 and N
D = p
f as it is during melting with N
C = p
f and N
D = 0. When Q
g and Q
b are closely matched, dissipative heating exerts an important control on the quantity of liquid to be transported. With N
C = 0 during freezing, D increases rapidly as N
D approaches the limiting value |NQ
|W
0/W
s. Values of D/(l − b) plotted in Figure 5b are the largest possible, with p
f > N > 0 everywhere between the conduit and divide. When N > 0 everywhere, for larger D a fringe is expected to form; the fringe is located near the divide when freezing takes place and near the conduit when melting takes place.

Fig. 5. (a) ![]() as a function of Q
b with Q
g = 60 mW m−2. The solid line shows the predictions of Equation (13) (where W
s = 10 m a−1) and the dashed lines depict the predictions of Equation (14). Between the vertical dotted lines,
as a function of Q
b with Q
g = 60 mW m−2. The solid line shows the predictions of Equation (13) (where W
s = 10 m a−1) and the dashed lines depict the predictions of Equation (14). Between the vertical dotted lines, ![]() and freezing takes place with D ≫ d. (b) The drainage divide distance D/(l − b) as a function of Q
b for the same conditions as in (a).
and freezing takes place with D ≫ d. (b) The drainage divide distance D/(l − b) as a function of Q
b for the same conditions as in (a).
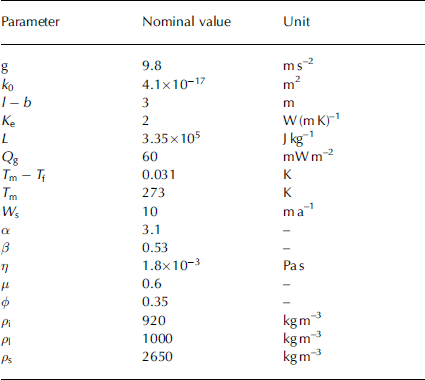
Table 2. Nominal parameters used for the calculations presented here. Values of T m − T f , k 0, α and β are for Chena silt (Reference Andersland and LadanyiAndersland and Ladanyi, 2004). These parameter values imply that the pressure scale p f ≈ 35 kPa, the velocity scale W 0 ≈ 130 m a −1 and the distance scale d ≈ 11 m. With the nominal value of Q g, NQ ranges from NQ ≈ 24 kPa when Q b =0 to NQ ≈ −24 kPa when Q b = 120 mW m −2
As suggested by Figure 5, the drainage behavior is particularly sensitive to small changes in parameter values when Q
b exceeds Q
g by only a small amount. Figure 6 illustrates this further with several effective stress profiles calculated using Q
b = 63.3 mW m−2, D = 20(l − b) and the closely spaced values of N
D/p
f listed in the legend. Although the basal heat flux is sufficient to remove the geothermal heat, frictional heating still leads to net basal melting when Q
b <Q
g + N
D
μW
s. Hence, although Q
b > Q
g is the same in each of the calculations shown in Figure 5, only the smallest two values of N
D/p
f are low enough to allow net freezing to the glacier base. The value of N
D/p
f = 0.5 was chosen so that Q
b = Q
g +μW
s
N
D and no net fluid flow is required. Slightly higher values of N
D/p
f produce frictional melting and require N to increase towards the drainage conduit at x = 0. This suggests that when Q
b and Q
g are similar in size, small changes in the effective stress at a drainage divide have the potential to produce major reorganizations in the subglacial flow that are accompanied by disproportionately large changes in ![]() .
.

Fig. 6. Effective stress profiles for several values of N
D/p
f in the transitional region with Q
b ≈ Q
g + μN
D
W
s. For the calculations shown here, ![]() ranges from a minimum of approximately 0.435 (bottom curve) to a maximum of 0.565 (top curve).
ranges from a minimum of approximately 0.435 (bottom curve) to a maximum of 0.565 (top curve).
Fringe present: h > 0
When N > p f , the local basal equilibrium considerations discussed above require that a partially frozen fringe form, as described by Equation (2) and shown schematically in Figure 1c. Reference RempelRempel (2008) showed that h can be approximated reasonably well when the temperature gradient is treated as constant and the details of the temperature profile are neglected. Using Equation (3) to obtain the steady-state freezing rate, an estimate of the fringe thickness h is determined as the solution to

Where T l ≈ Tf − (Q g + Q f)h/K e.
Figure 7 depicts solutions to Equation (15) using the soil parameters for Chena silt given in Table 2 to obtain S i and k from Equations (8) and (9). N = p f at h = 0 and, as h increases, the effective stress at the fringe base initially increases to support the added weight of till. When Q b < (Q g + Q f) so that V < 0 and net melting takes place, water is driven downwards through the fringe. This implies that the fluid pressure gradient through the fringe must be less than hydrostatic so the last term in Equation (15) is positive and N increases monotonically as h gets larger. When Q b > (Q g + Q f ), the fluid pressure gradient through the fringe must be elevated to drive flow upwards and N begins to decrease once h is sufficiently large. The solid curves in Figure 7 show predictions for h when W s = 10 m a−1 and dissipation along the assumed sliding surface at the base of the fringe enhances the local heat supply. A comparison with the dashed curves for W s = 0 reveals that increased dissipation is associated with higher N at any given value of h.

Fig. 7. Approximate steady-state fringe thickness h as a function of effective stress N, with Q g = 60 mW m−2 and the values of Q b noted in the legend. Dissipative heating is modeled with Q f = μNW s, and the temperature gradient is approximated as uniform and equal to (Q g + Q f )/K e.
In regions along the glacier base where a fringe is present, the steady-state mass-balance condition from Equations (5) and (7) can be written as

Here, the seepage flux in the down-glacier direction is again assumed to vary gradually in comparison with that in the cross-glacier direction. Solutions to Equation (16) are required to match with solutions to Equation (11) at x = D f, where N = p f and h = 0. Further details of the predicted behavior are summarized in sections C–F of Table 1.
Figure 8 shows predicted values for the scaled average effective stress ![]() as a function of the scaled distance to the drainage divide D/(l − b). The solid curves labeled with their corresponding Q
b values are for the default case where Q
f = μNW
s and W
s = 10m a −1. For comparison, the dashed curves in Figure 8 show the predicted behavior when Q
f = 0. For the case of a temperate glacier with a basal heat flux of Q
b = 0,
as a function of the scaled distance to the drainage divide D/(l − b). The solid curves labeled with their corresponding Q
b values are for the default case where Q
f = μNW
s and W
s = 10m a −1. For comparison, the dashed curves in Figure 8 show the predicted behavior when Q
f = 0. For the case of a temperate glacier with a basal heat flux of Q
b = 0, ![]() increases monotonically with D until it reaches 2p
f near D ≈ 3(l − b). The lower solid curve for Q
b = 30 mW m −2 predicts similar behavior, but with a slower monotonic rise in
increases monotonically with D until it reaches 2p
f near D ≈ 3(l − b). The lower solid curve for Q
b = 30 mW m −2 predicts similar behavior, but with a slower monotonic rise in ![]() with D. Note that Q
b < Q
g for this case as well, so net melting takes place. The curve terminates at
with D. Note that Q
b < Q
g for this case as well, so net melting takes place. The curve terminates at ![]() and D/(l − b) ≈ 4 because the fringe becomes thick enough at this point to encompass the entire nominal till thickness of l − b = 3 m. For the case where Q
b = 0, h ≈ l − b = 3 m when D ≈ 3(l − b) and
and D/(l − b) ≈ 4 because the fringe becomes thick enough at this point to encompass the entire nominal till thickness of l − b = 3 m. For the case where Q
b = 0, h ≈ l − b = 3 m when D ≈ 3(l − b) and ![]() . Calculations for cases with Q
b ≤ Q
g were performed for an assumed effective stress at the divide of N
D = 0. Higher choices of N
D would produce higher values of
. Calculations for cases with Q
b ≤ Q
g were performed for an assumed effective stress at the divide of N
D = 0. Higher choices of N
D would produce higher values of ![]() for a particular choice of D. These calculations demonstrate that when melting takes place, only a limited channel spacing is permitted before the entire till layer is infiltrated with ice.
for a particular choice of D. These calculations demonstrate that when melting takes place, only a limited channel spacing is permitted before the entire till layer is infiltrated with ice.

Fig. 8. Variation in ![]() with D/(l − b) for Q
g = 60 mW m−2 with the values of Q
b listed in the legend. The calculations involving net freezing at the glacier base (i.e. Q
b = 90 and 120 mW m−2) were made with N(0) = N
C = 0.
with D/(l − b) for Q
g = 60 mW m−2 with the values of Q
b listed in the legend. The calculations involving net freezing at the glacier base (i.e. Q
b = 90 and 120 mW m−2) were made with N(0) = N
C = 0.
Two sets of calculations are shown in Figure 8 with Q
b > Q
g so that net freezing occurs at the glacier base. In each case, the effective stress at the conduit is set to N
C = 0. With increases in D, ![]() increases initially until the threshold from Figure 5b is reached for that particular value of Q
b, at which point a fringe first begins to form at x = D
f = D. Increases in D are possible for a steady-state system with a fringe that extends from the divide to ever smaller values of D
f. A maximum steady-state divide distance is soon reached, however. Further decreases in D
f are also accompanied by decreases in D so that with the same value of N
C (i.e. N
C = 0 here) there are two possible steady-state values of
increases initially until the threshold from Figure 5b is reached for that particular value of Q
b, at which point a fringe first begins to form at x = D
f = D. Increases in D are possible for a steady-state system with a fringe that extends from the divide to ever smaller values of D
f. A maximum steady-state divide distance is soon reached, however. Further decreases in D
f are also accompanied by decreases in D so that with the same value of N
C (i.e. N
C = 0 here) there are two possible steady-state values of ![]() for any particular D. The higher steady-state
for any particular D. The higher steady-state ![]() is for the case in which the fringe extends over a larger portion of the glacier base.
is for the case in which the fringe extends over a larger portion of the glacier base.
As shown here, the range of possible steady-state values of D and ![]() is greater for cases of freezing with Q
b closer to Q
g. These results show that when net freezing occurs, the maximum steady-state channel spacing does not necessarily correspond to the entire till layer being infiltrated with ice. Instead, for the cases examined here, the maximum D is connected with the limit to the steady-state N that can be achieved (refer to the left-most curves in Fig. 7) as a result of the reduced permeability to vertical fluid transport through the fringe.
is greater for cases of freezing with Q
b closer to Q
g. These results show that when net freezing occurs, the maximum steady-state channel spacing does not necessarily correspond to the entire till layer being infiltrated with ice. Instead, for the cases examined here, the maximum D is connected with the limit to the steady-state N that can be achieved (refer to the left-most curves in Fig. 7) as a result of the reduced permeability to vertical fluid transport through the fringe.
The horizontal solid line in Figure 8 with ![]() corresponds to the case where Q
b = Q
g with N
D = 0. With no imbalance between the background geothermal heat flow and the basal heat flux, since no dissipative heating is expected when N = 0, no net water transport is required, the effective stress is constant everywhere and
corresponds to the case where Q
b = Q
g with N
D = 0. With no imbalance between the background geothermal heat flow and the basal heat flux, since no dissipative heating is expected when N = 0, no net water transport is required, the effective stress is constant everywhere and ![]() .
.
Figure 4 shows profiles of N=p
f and h=(l − b) for the parameters used to produce Figure 8. For the cases where Q
b < Q
g so that melting takes place, with fixed values of D and N
D (calculations here were made with D = 2(l − b) and N
D = 0) the requirements for fluid drainage admit a unique profile of N/p
f . As expected from the values of ![]() shown in Figure 8, the effective stress increases towards the drainage conduit more rapidly when Q
b = 0 than when Q
b = 30 mW m−2. This is because larger fluid fluxes accompany more vigorous melting and require correspondingly larger effective stress gradients to drive flow. The fringe depth near the drainage conduit is greater when N/p
f is higher there, and so a larger volume of till is expected to be frozen to the glacier base when Q
b is low. The presence of deep frozen regions near the drainage conduit tends to restrict fluid access. Since the fringe depth is reduced for lower conduit spacings, this suggests a potential mechanism for setting the spacing of drainage conduits. Note that more closely spaced conduits not only have the advantage that fluid access is not restricted by thick fringes, but also allow for lower
shown in Figure 8, the effective stress increases towards the drainage conduit more rapidly when Q
b = 0 than when Q
b = 30 mW m−2. This is because larger fluid fluxes accompany more vigorous melting and require correspondingly larger effective stress gradients to drive flow. The fringe depth near the drainage conduit is greater when N/p
f is higher there, and so a larger volume of till is expected to be frozen to the glacier base when Q
b is low. The presence of deep frozen regions near the drainage conduit tends to restrict fluid access. Since the fringe depth is reduced for lower conduit spacings, this suggests a potential mechanism for setting the spacing of drainage conduits. Note that more closely spaced conduits not only have the advantage that fluid access is not restricted by thick fringes, but also allow for lower ![]() as shown in Figure 8.
as shown in Figure 8.
For the cases where Q
b > Q
g + Q
f so that freezing takes place, two steady-state N/p
f profiles are possible for sufficiently small values of D/(l − b) with fixed N
C (calculations shown in Fig. 4 were made with N
C = 0). Only a restricted range of steady-state conduit spacings is possible for a given value of Q
b > Q
g. For example, the N/p
f profile with lower ![]() for Q
b = 90mW m −2 requires no fringe formation. However, the case with lower
for Q
b = 90mW m −2 requires no fringe formation. However, the case with lower ![]() for Q
b = 120mWm −2 requires a fringe that extends to nearly one-fifth of the depth of the till layer. This difference in behavior can be traced to the larger fluid supply rate required of the more vigorous freezing in the latter case.
for Q
b = 120mWm −2 requires a fringe that extends to nearly one-fifth of the depth of the till layer. This difference in behavior can be traced to the larger fluid supply rate required of the more vigorous freezing in the latter case.
The effective stress gradient vanishes at the drainage divide where flow in the ![]() direction ceases. As indicated by Equation (16), this happens when either dh/dx = 0 or dN/dh = (ρ
s − ρ
i)g(1 − ϕ). Further analysis shows that the former condition always applies for the lower N/p
f profile at a particular Q
b > Q
g + Q
f and N
C. Gradients in h at the drainage divide also vanish for the upper N/p
f profiles when
direction ceases. As indicated by Equation (16), this happens when either dh/dx = 0 or dN/dh = (ρ
s − ρ
i)g(1 − ϕ). Further analysis shows that the former condition always applies for the lower N/p
f profile at a particular Q
b > Q
g + Q
f and N
C. Gradients in h at the drainage divide also vanish for the upper N/p
f profiles when ![]() is sufficiently close to its maximum shown in Figure 8 for a particular Q
b > Q
g + Q
f. However, as shown in Figure 4b by the lower curve for Q
b = 90 mW m−2, dh/dx ≠ 0 for the higher of the two N/p
f profiles at this basal heat flux. A linear stability analysis shows that those steady-state solutions with dN=dh =(ρ
s − ρ
i)g(1 − ϕ) are only marginally stable. Perturbations that lead to slight increases in h at the divide are expected to cause N to drop slightly. This will reduce the frictional heat input and allow more freezing to take place until, eventually, the entire sediment layer becomes frozen. In other words, a steady state with dh/dx ≠ 0 at the drainage divide is not expected to persist.
is sufficiently close to its maximum shown in Figure 8 for a particular Q
b > Q
g + Q
f. However, as shown in Figure 4b by the lower curve for Q
b = 90 mW m−2, dh/dx ≠ 0 for the higher of the two N/p
f profiles at this basal heat flux. A linear stability analysis shows that those steady-state solutions with dN=dh =(ρ
s − ρ
i)g(1 − ϕ) are only marginally stable. Perturbations that lead to slight increases in h at the divide are expected to cause N to drop slightly. This will reduce the frictional heat input and allow more freezing to take place until, eventually, the entire sediment layer becomes frozen. In other words, a steady state with dh/dx ≠ 0 at the drainage divide is not expected to persist.
4. Discussion
The simple models presented here illustrate how subglacial drainage systems impose limits on the steady-state behavior of glaciers and ice sheets. For example, the average effective stress ![]() is predicted to be limited to a small multiple of the pressure scale p
f that marks the local value of the effective stress N at which ice first invades the pore space. Even for tills with very small pore apertures, p
f is typically expected to be less than 1 bar; coarse-grained substrates can be associated with values of p
f that are vanishingly small. There are many glaciological settings in which the inferred average basal shear stress
is predicted to be limited to a small multiple of the pressure scale p
f that marks the local value of the effective stress N at which ice first invades the pore space. Even for tills with very small pore apertures, p
f is typically expected to be less than 1 bar; coarse-grained substrates can be associated with values of p
f that are vanishingly small. There are many glaciological settings in which the inferred average basal shear stress ![]() is low enough to be consistent with till operating as a Coulomb plastic material, with
is low enough to be consistent with till operating as a Coulomb plastic material, with ![]() . There are also circumstances in which the inferred
. There are also circumstances in which the inferred ![]() is sufficiently large that it greatly exceeds expected values of p
f . This could imply that the subglacial sediments are particularly fine-grained or are perhaps mantled by fine-grained material so that p
f is unusually large; it could also imply that thick fringe layers extend beneath the glacier.
is sufficiently large that it greatly exceeds expected values of p
f . This could imply that the subglacial sediments are particularly fine-grained or are perhaps mantled by fine-grained material so that p
f is unusually large; it could also imply that thick fringe layers extend beneath the glacier.
A further possibility that has not been explored here, but often seems likely to hold, is that the inferred average basal shear stress is dominated by the effects of basal topography, much as is generally accepted to be the case for glaciers that slide over hard beds (e.g. Reference KambKamb, 1970; Reference PatersonPaterson, 1994). The modeling framework employed here could be extended to explore the effects of bed undulations on subglacial freezing behavior to quantify their influence on τ b. Strong field evidence for the importance of subglacial heterogeneity in τ b includes the inferred ‘sticky spots’ that are thought to be responsible for temporal variations in sliding rate along the Siple Coast ice plain (Reference Bindschadler, King, Alley, Anandakrishnan and PadmanBindschadler and others, 2003).
When no fringe is present, for a given conduit spacing the average effective stress ![]() is predicted to decrease with increased sliding speed W
s. Such behavior is contrary to what has sometimes been inferred and modeled for tills that appear to deform in a viscous fashion. In many circumstances the effects of basal topography are expected to produce enhanced
is predicted to decrease with increased sliding speed W
s. Such behavior is contrary to what has sometimes been inferred and modeled for tills that appear to deform in a viscous fashion. In many circumstances the effects of basal topography are expected to produce enhanced ![]() with increased Ws, and this may be partly responsible for the inferred behavior. Moreover, a comparison between the solid and dashed curves in Figure 8 indicates that when a fringe is present and freezing takes place,
with increased Ws, and this may be partly responsible for the inferred behavior. Moreover, a comparison between the solid and dashed curves in Figure 8 indicates that when a fringe is present and freezing takes place, ![]() is lower for steady sliding and dissipation at finite W
s than it is when W
s = 0. The opposite situation arises for the case where melting takes place with a fringe present and the steady
is lower for steady sliding and dissipation at finite W
s than it is when W
s = 0. The opposite situation arises for the case where melting takes place with a fringe present and the steady ![]() is higher with dissipation than without.
is higher with dissipation than without.
In circumstances where more rapid sliding produces lower sliding resistance, the potential exists for a runaway effect that could be responsible for producing regions of localized fast glacier flow. The steady-state predictions shown here suggest that very low values of ![]() can be associated with cases of intermediate basal heat flow, when Q
g < Q
b < Q
g +μW
s
N
D and conduit spacings are large because very little meltwater is generated. It is commonly assumed that fast-flowing regions such as ice streams require rapid melt generation, yet detailed studies suggest that the situation may be more complicated. In some cases (e.g. beneath Whillans Ice Stream, West Antarctica), the heat-flow regime curently supports relatively low melting rates and even areas with net freezing (Reference Joughin, Tulaczyk, MacAyeal and EngelhardtJoughin and others, 2004).
can be associated with cases of intermediate basal heat flow, when Q
g < Q
b < Q
g +μW
s
N
D and conduit spacings are large because very little meltwater is generated. It is commonly assumed that fast-flowing regions such as ice streams require rapid melt generation, yet detailed studies suggest that the situation may be more complicated. In some cases (e.g. beneath Whillans Ice Stream, West Antarctica), the heat-flow regime curently supports relatively low melting rates and even areas with net freezing (Reference Joughin, Tulaczyk, MacAyeal and EngelhardtJoughin and others, 2004).
The calculations shown here and illustrated in Figure 6 are consistent with the theory that small changes can produce significant disruptions to the steady behavior. It is interesting to speculate whether the dynamics of seepage flows may bear significant responsibility for the transient behavior of ice streams.
The conduit spacing D has been treated here as given, whereas in practice this key characteristic of hydrological networks should be determined dynamically. Reference Walder and FowlerWalder and Fowler (1994) suggested that conduit spacing is set by a piping condition, where seepage fluxes are limited by erosive processes at conduit boundaries. Reference ShoemakerShoemaker (1986) explored the potential for piping at the ice-sheet terminus to regulate the conduit spacing by limiting the maximum size of hydraulic gradients, but favored a mechanism in which spacing was set by a maximum in the allowable pressure drop from conduit to divide. The current model also suggests that the pressure change from conduit to divide limits the maximum allowable D, and further constrains what this maximum allowable pressure change should be. When Q b < Q g + Q f so that net melting occurs, the conduit spacing reaches its limiting value when N C rises sufficiently for the fringe to penetrate the entire depth of the till layer (i.e. h = l − b; see Fig. 8). By contrast, under freezing conditions with Q b > Q g + Q f , the steady conduit spacing attains a stable maximum at intermediate D that is controlled by the permeability structure of the partially frozen sediments of the fringe once it reaches a finite thickness (that can still be much lower than l − b).
It is interesting to note that for a fixed conduit spacing, the resistance to fluid flow through the fringe can be sufficient to cause ![]() for freezing conditions with Q
b > Q
g + Q
f to be significantly lower than
for freezing conditions with Q
b > Q
g + Q
f to be significantly lower than ![]() for melting conditions with Q
b < Q
g + Q
f . This behavior is contrary to what is commonly assumed based on the poroelastic properties of tills. Gradients in void fraction are not expected to be significant for the steady behavior examined here and so have been neglected, whereas temporal changes in void fraction can have a more important influence on transient events.
for melting conditions with Q
b < Q
g + Q
f . This behavior is contrary to what is commonly assumed based on the poroelastic properties of tills. Gradients in void fraction are not expected to be significant for the steady behavior examined here and so have been neglected, whereas temporal changes in void fraction can have a more important influence on transient events.
For the calculations presented here, p f was taken as that corresponding to Chena silt. Other sediments are expected to have larger or smaller values of p f , depending on the sizes of their pore apertures. For example, with pore apertures of characteristic radius R p, p f ≈ 2γ il/Rp varies from 70 kPa to 7 kPa to 0.7 kPa as R p varies from 1 μm to 10 μm to 100 μm. The value of the unfrozen permeability k 0 ≈ 4.1 × 10 −17 m2 for Chena silt is towards the low end of values typically quoted for tills. As noted in the Appendix, the depth-integrated seepage flow models presented here are expected to perform better for higher values of k 0, which tend to promote larger aspect ratios D/(l − b).
Topographic variations and heterogeneous basal properties in natural glacier systems produce a far richer variety of behavior than the elementary models shown here could ever hope to capture. Nevertheless, the basic considerations employed here can be used as a guide for future studies aiming to explore the essential features of drainage interactions in more realistic settings.
5. Conclusions
The average effective stress ![]() beneath soft-bedded glaciers is constrained by subglacial drainage requirements. When flow between most of the glacier base and major conduits occurs primarily through seepage flows, the conduit spacing and heat-flow regime strongly influence
beneath soft-bedded glaciers is constrained by subglacial drainage requirements. When flow between most of the glacier base and major conduits occurs primarily through seepage flows, the conduit spacing and heat-flow regime strongly influence ![]() . Beyond a critical level of
. Beyond a critical level of ![]() , the hydraulic gradients required for seepage transport lead to local values of N > p
f so that ice penetrates the pore space to form a fringe of partially frozen sediment with thickness h, extending beneath the glacier base. When net melting takes place, the fringe is thickest near drainage conduits and higher values of
, the hydraulic gradients required for seepage transport lead to local values of N > p
f so that ice penetrates the pore space to form a fringe of partially frozen sediment with thickness h, extending beneath the glacier base. When net melting takes place, the fringe is thickest near drainage conduits and higher values of ![]() require increases in h that can eventually lead to freezing of the entire till thickness. When net freezing takes place, the fringe is thickest near drainage divides and there is a maximum conduit spacing that can support steady-state behavior. For any conduit spacing below this maximum, two steady-state values of
require increases in h that can eventually lead to freezing of the entire till thickness. When net freezing takes place, the fringe is thickest near drainage divides and there is a maximum conduit spacing that can support steady-state behavior. For any conduit spacing below this maximum, two steady-state values of ![]() are possible, the lower of which is always stable. The higher steady-state
are possible, the lower of which is always stable. The higher steady-state ![]() has a more extensive fringe that can be unstable to small perturbations in its thickness. This suggests the potential for transient freezing through the till layer that could produce dramatic changes in basal shear stress.
has a more extensive fringe that can be unstable to small perturbations in its thickness. This suggests the potential for transient freezing through the till layer that could produce dramatic changes in basal shear stress.
Appendix
Effects of vertical seepage transport
It is useful to consider more closely the circumstances under which the depth-integrated model should perform at its best. The length scale d emerged in the previous sections as the natural length scale for hydrologically significant changes in N when Q f > 0. Further calculations confirm that for |N D − N C| comparable to p f or greater, D ≫ l − b when d ≫ l − b. This occurs when W 0 ≫ W s or equivalently when ρ l k 0 L/[μWsη (l − b) ≫ 1. Substituting for the properties of the water system summarized in Table 2 and using the nominal friction coefficient of μ = 0.6, this implies that d ≫ l − b when k 0/[W s(l − b) ] ≫ 3 × 10 −12 s. The seepage transport is best approximated by the depth-integrated treatment for conditions of less rapid sliding over more permeable sediments that are present in thinner layers. The depth-integrated treatment is also very good for cases where Q b and Q g are very closely matched, as suggested by the dotted vertical boundaries in the middle of Figure 5b.
The model results presented in Table 1 treated the seepage transport using depth-integrated equations that are expected to be a good approximation when D ≫ l − b. In many of the cases considered here, however, the divide distance D is only larger than the till thickness l − b by a modest amount. While the qualitative behavior described by the depth-integrated equations is expected to be robust, vertical seepage transport should affect the detailed quantitative behavior. A few calculations are useful for illustrating the overall effects.
In Figure 9, levels of ![]() as a function of D/(l − b) are compared for the one-dimensional (1-D) depth-integrated predictions of Table 1 and predictions of more complete (2-D) finite-difference calculations in which either the conduit extends the full 3 m depth of the till (solid curve), or the conduit extends only 1 m down from the top of the 3 m thick till layer (dot-dashed curve). The 2-D model solves Laplace’s equation for N on a rectangular domain, with no flux boundary conditions at the base and the divide. Along the x = 0 axis where the conduit is present, N is set to N
C at (x, z) = (0, l) with a hydrostatic gradient extending downwards to the conduit base. A no-flux condition is set beneath the conduit for the case where it penetrates only the top meter of the 3 m till depth. The mass-balance condition is applied along the rest of the glacier boundary for 0 ≤ x ≤ D and z = l, where melting acts as a water source or freezing acts as a water sink. By comparing the solid curves with the dashed curves it can be seen that when the conduit extends the full depth of the till layer, the differences between the 2-D and 1-D predictions for
as a function of D/(l − b) are compared for the one-dimensional (1-D) depth-integrated predictions of Table 1 and predictions of more complete (2-D) finite-difference calculations in which either the conduit extends the full 3 m depth of the till (solid curve), or the conduit extends only 1 m down from the top of the 3 m thick till layer (dot-dashed curve). The 2-D model solves Laplace’s equation for N on a rectangular domain, with no flux boundary conditions at the base and the divide. Along the x = 0 axis where the conduit is present, N is set to N
C at (x, z) = (0, l) with a hydrostatic gradient extending downwards to the conduit base. A no-flux condition is set beneath the conduit for the case where it penetrates only the top meter of the 3 m till depth. The mass-balance condition is applied along the rest of the glacier boundary for 0 ≤ x ≤ D and z = l, where melting acts as a water source or freezing acts as a water sink. By comparing the solid curves with the dashed curves it can be seen that when the conduit extends the full depth of the till layer, the differences between the 2-D and 1-D predictions for ![]() are minor even at divide distances D that are comparable to l − b. The comparison is less satisfactory when the conduit extends only a fraction of the till depth, as shown by the dot-dashed curve. However, the depth-integrated 1-D predictions still reflect the overall trends. In comparison to the 2-D predictions, the depth-integrated model underestimates
are minor even at divide distances D that are comparable to l − b. The comparison is less satisfactory when the conduit extends only a fraction of the till depth, as shown by the dot-dashed curve. However, the depth-integrated 1-D predictions still reflect the overall trends. In comparison to the 2-D predictions, the depth-integrated model underestimates ![]() for cases of net freezing with Q
b > Q
g and overestimates
for cases of net freezing with Q
b > Q
g and overestimates ![]() for cases of net melting with Q
b < Q
g.
for cases of net melting with Q
b < Q
g.

Fig. 9.
![]() as a function of D/(l − b) calculated while treating the seepage flow as 2-D and for the depth-integrated 1-D model (dashed). Decreasing
as a function of D/(l − b) calculated while treating the seepage flow as 2-D and for the depth-integrated 1-D model (dashed). Decreasing ![]() values with D/(l − b) are for melting conditions with Q
b = 30 mW m −2 and N
C = p
f . Increasing values are for freezing conditions with Q
g = 90 mW m −2 and N
C = 0. Calculations were terminated for the melting cases once D was sufficiently large that N
D ≈ 0 and for freezing cases when N
D ≈ p
f .
values with D/(l − b) are for melting conditions with Q
b = 30 mW m −2 and N
C = p
f . Increasing values are for freezing conditions with Q
g = 90 mW m −2 and N
C = 0. Calculations were terminated for the melting cases once D was sufficiently large that N
D ≈ 0 and for freezing cases when N
D ≈ p
f .

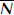 , which is controlled by the distribution of water pressure at the bed. Major subglacial conduits that facilitate large-scale water transport are expected to be predominantly aligned with the direction of maximum hydraulic gradient, which is normally parallel to the slope of the glacier surface. When the basal heat flow promotes net melting or freezing, seepage transport can enable water exchange between these conduits and the rest of the basal surface area. For a simple glacier geometry with subglacial conduits that are aligned parallel to a uniform slope, the seepage transport is driven primarily by gradients in effective stress. Balance equations determine how
, which is controlled by the distribution of water pressure at the bed. Major subglacial conduits that facilitate large-scale water transport are expected to be predominantly aligned with the direction of maximum hydraulic gradient, which is normally parallel to the slope of the glacier surface. When the basal heat flow promotes net melting or freezing, seepage transport can enable water exchange between these conduits and the rest of the basal surface area. For a simple glacier geometry with subglacial conduits that are aligned parallel to a uniform slope, the seepage transport is driven primarily by gradients in effective stress. Balance equations determine how 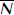 varies with conduit spacing and the heat-flow regime. Considerations of thermodynamic equilibrium require that ice penetrates the pore space at high effective stress. Even when the glacier base experiences net melting, for a given heat-flow regime there are limits on the conduit spacing that can be attained before a finite till layer becomes partially frozen throughout. During net freezing, the resistance to flow through partially frozen sediments limits the steady-state conduit spacing. The partially frozen zone can actually be restricted to smaller thicknesses when the freezing rate is greater.
varies with conduit spacing and the heat-flow regime. Considerations of thermodynamic equilibrium require that ice penetrates the pore space at high effective stress. Even when the glacier base experiences net melting, for a given heat-flow regime there are limits on the conduit spacing that can be attained before a finite till layer becomes partially frozen throughout. During net freezing, the resistance to flow through partially frozen sediments limits the steady-state conduit spacing. The partially frozen zone can actually be restricted to smaller thicknesses when the freezing rate is greater.










