Introduction
The propagation of ocean swells into a floating ice cover has led, in at least a few recorded instances, to the sudden break-up of the ice cover into smaller ice floes (Asplin and others, Reference Asplin, Galley, Barber and Prinsenberg2012; Collins and others, Reference Collins, Rogers, Marchenko and Babanin2015; Kohout and others, Reference Kohout, Williams, Toyota, Lieser and Hutchings2016). In these works, the sudden break-up of first-year and multi-year ice was observed due to wave action which is discussed in Ardhuin and others (Reference Ardhuin, Otero, Merrifield, Grouazel and Terrill2020). These observations raise a question about the effect of cyclic loading on the mechanical behavior of ice. From a practical perspective, this question is relevant not only to floating ice covers that form on cold lakes and oceans and these were investigated previously in the laboratory and in situ in the field (Mellor and Cole, Reference Mellor and Cole1981; Nixon and Smith, Reference Nixon and Smith1987; Cole, Reference Cole1990, Reference Cole1998; Haynes and others, Reference Haynes, Kerr and Martinson1993; Cole and Durell, Reference Cole and Durell1995; Haskell and others, Reference Haskell, Robinson and Langhorne1996; Langhorne and Haskell, Reference Langhorne and Haskell1996; Bond and Langhorne, Reference Bond and Langhorne1997; Weber and Nixon, Reference Weber and Nixon1997; Cole and others, Reference Cole1998; Gupta and others, Reference Gupta, Bergström and Picu1998; Langhorne and others, Reference Langhorne, Squire, Fox and Haskell1998, Reference Langhorne, Squire and Haskell1999, Reference Langhorne, Squire, Fox and Haskell2001; Iliescu and Schulson, Reference Iliescu and Schulson2002; Cole and Dempsey, Reference Cole and Dempsey2004), but also to the stability of floating ice shelves (Holdsworth, Reference Holdsworth1969; Vinogradov and Holdsworth, Reference Vinogradov and Holdsworth1985; Sergienko, Reference Sergienko2010), accretion of atmospheric ice on power transmission lines (Kermani and Farzaneh, Reference Kermani and Farzaneh2009) and, under tidal forcing of an extraterrestrial origin, the strength of the icy crust of Jupiter's Europa and of Saturn's Enceladus (Burns and Matthews, Reference Burns and Matthews1986; Hammond and others, Reference Hammond, Barr, Cooper, Caswell and Hirth2018). With that in mind, we recently performed systematic experiments (at −25 to −3o C at 0.03–2 Hz) on the behavior under 4-point cyclic loading of columnar-grained S2 fresh water ice produced in the laboratory and loaded across the long axis of the columns (Iliescu and others, Reference Iliescu, Murdza, Schulson and Renshaw2017; Murdza and others, Reference Murdza, Schulson and Renshaw2018, Reference Murdza, Schulson and Renshaw2019, Reference Murdza, Schulson and Renshaw2020). We found that the flexural strength increased upon cycling, scaling linearly with the amplitude of the outer-fiber stress (0.1–2.6 MPa) and reaching a factor of two or more greater than the noncycled strength. Is this behavior, we wondered, a characteristic also of ice produced under natural conditions? To explore this point, we performed similar experiments on lake ice. This paper describes our results.
Procedure
We harvested the ice from the ~50 cm thick cover on a lake in the Arctic, located near Mine 7 in Longyearbyen, Svalbard. The ice was characterized by columnar-shaped grains of 17 ± 3 mm diameter, Figure 1, an S2 growth texture (c-axis was randomly oriented within the horizontal plane of the parent ice cover and confined within ~15° to that plane), and a density of 915 kg m−3. From large (~120 cm × 70 cm × 50 cm) blocks cut from the cover and then transported to and stored at UNIS, we fabricated plate-shaped specimens of dimensions h ~ 45 mm in thickness (parallel to the long axis of the grains), b ~ 100 mm in width and l ~ 600 mm in length. The specimens were equilibrated at −12 °C and then nonreversely loaded across the columns at 0.1 Hz at an outer-fiber stress in the range from ~ 0.1 to ~ 0.7 MPa, using a custom-built 3-point bending rig, Figure 2, attached to a uniaxial loading system termed ‘Knekkis’ (for details on Knekkis see Nanetti and others (Reference Nanetti, Marchenko and Høyland2008); Sukhorukov and Marchenko (Reference Sukhorukov and Marchenko2014)). The specimens were free from cracks, at least of a size detectable by the unaided eye, but contained a few narrow (< 1 mm dia.) air channels oriented parallel to the long axis of the grain columns.

Fig. 1. Photographs showing the microstructure of lake ice: horizontal (a) and vertical (b) thin sections.
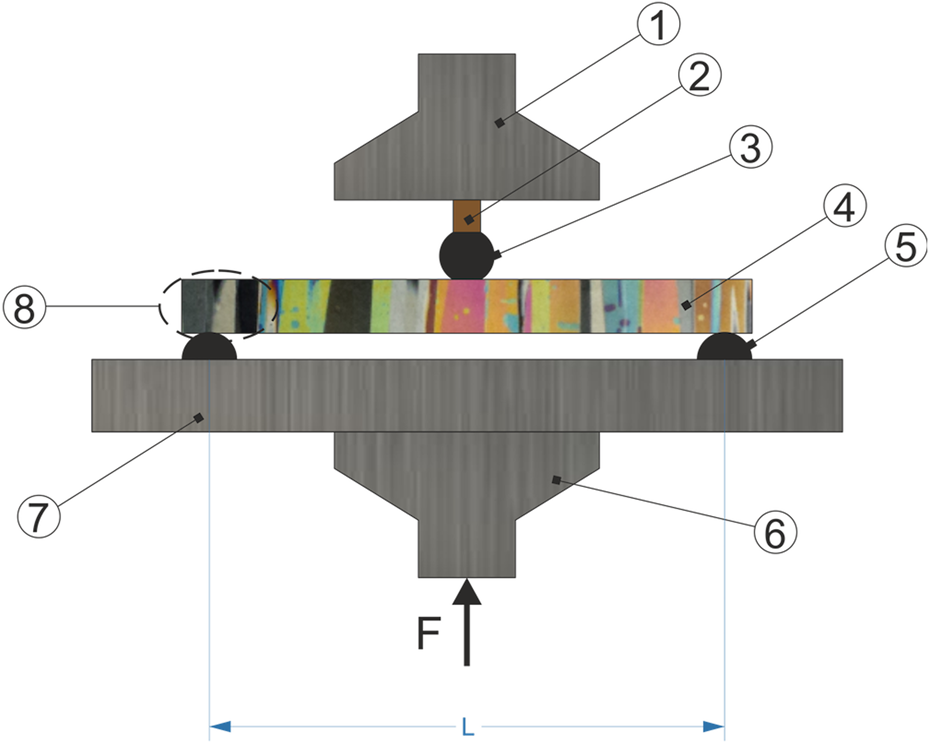
Fig. 2. Sketch of the three-point bending apparatus connected to a ‘Knekkis’ mechanical testing system: 1 – immobile steel plate; 2 – HBM load cell; 3 – mid-loading span; 4 – ice specimen; 5 – outer loading span; 6 – loading press; 7 – steel plate; 8 – schematics of columns within the ice specimen. The upper immobile part 1 is attached to the frame of the machine while the mobile lower part 6 is attached through a fatigue-rated load cell to the piston.
To load and then unload the specimen, the mechanical actuator of ‘Knekkis’ was driven up and down under displacement control with the displacement limited in both directions. In addition to a built-in load cell, an external more accurately calibrated HBM load cell was placed between the middle loading span and the press. The results showed there was no significant difference in measurements made using the two load cells. The displacement of the top surface of the ice plate was measured using three calibrated HBM LVDT gauges and the outer-fiber stress σ f was calculated from the relationship:
where P denotes the applied load, L is the load span (460 mm) and b and h the dimensions noted above.
Results and observations
Firstly, we conducted three tests where the flexural strength of noncycled ice was measured. Table 1 lists the results. The average and Std dev. of the measured flexural strength are 1.52 ± 0.04 MPa which indicates good reproducibility. These values compare favorably with the values of 1.73 ± 0.25 MPa reported by Timco and O'Brien (Reference Timco and O'Brien1994) for S2 fresh water ice at temperatures below −4.5 °C and with the values of 1.67 ± 0.22 MPa reported by Murdza and others (Reference Murdza, Schulson and Renshaw2020) for S2 fresh water ice at −10 °C.
Table 1. Flexural strength of both noncycled and cycled lake ice samples

Subsequently, we cycled four specimens in a nonreversed manner for a certain number of cycles (up to 12 000) and then brought the ice to a forced monotonic failure by bending in the same sense as cycled. Table 1 lists the stress amplitude during cycling, the number of cycles imposed and the flexural strength after cycling. Figure 3 plots the flexural strength versus amplitude of outer-fiber stress and compares the present results with those obtained earlier (Murdza and others, Reference Murdza, Schulson and Renshaw2020) from laboratory-grown ice. Despite somewhat different loading conditions and a different origin of ice, specified in Table 2, the lake ice appears to behave similarly to the laboratory-grown ice under cycling: its flexural strength increases in an apparent linear manner as stress amplitude (and outer-fiber stress) increases.
Table 2. Comparison of the test setup and ice parameters between laboratory-grown ice (Murdza and others, Reference Murdza, Schulson and Renshaw2020) and present lake ice

a Density of ice grown in the same manner is taken from Golding and others (Reference Golding, Schulson and Renshaw2010).
b In the nonreversed experiments, frequency is lower by a factor of two than in the reversed experiments at the same conditions.
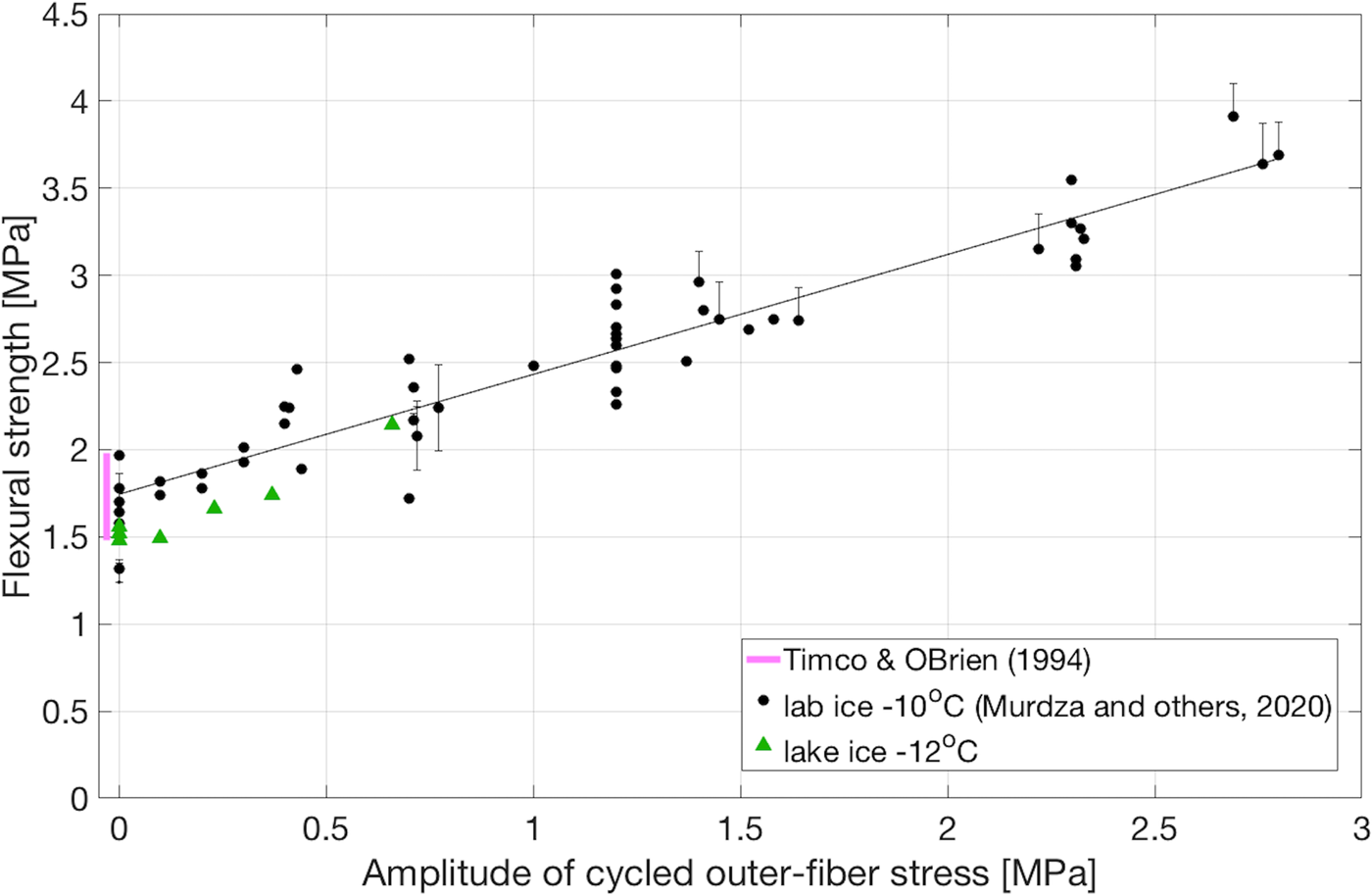
Fig. 3. Flexural strength of fresh water ice as a function of stress amplitude/average amplitude of outer-fiber stress during cycling. The solid pink line indicates the average flexural strength of noncycled fresh water ice plus and minus one standard deviation, i.e. 1.73 ± 0.25 MPa (Timco and O'Brien, Reference Timco and O'Brien1994). Black points represent laboratory tests presented in Murdza and others (Reference Murdza, Schulson and Renshaw2020) which were conducted on laboratory-grown fresh water ice at −10 °C and 0.1 mm s−1 outer-fiber center-point displacement rate in a reversed manner. Green points represent new tests on the lake ice. During all depicted tests the ice did not fail during cycling but was broken by applying one unidirectional displacement until failure occurred.
In all tests, failure occurred in the midpoint of the sample, i.e. beneath the mid-loading span. Interestingly, that this place is the most ‘strained’ zone within the sample given that the degree of strengthening depends on the outer-fiber stress amplitude and that the outer-fiber stress reaches its maximum in the midpoint of a specimen in 3-point bending test. Therefore, the location of ice failure is an important characteristic of an experiment as it may indicate the dependence of flexural strength on the stress amplitude. This is different from the 4-point bending test where the peak outer-fiber stress is produced along an extended region between inner loading spans and, therefore, failure occurs randomly within the middle section.
In contrast to experiments reported by Iliescu and others (Reference Iliescu, Murdza, Schulson and Renshaw2017) and Murdza and others (Reference Murdza, Schulson and Renshaw2020), where samples were cycled between two specified load limits, in the present experiments specimens were cycled between two specified displacement limits. We observed inelastic deformation during cycling and, as a result, both mean load and maximum load per cycle gradually decreased during cycling. Therefore, stresses in Figure 3 and Table 1 are the average amplitudes of outer-fiber stresses.
It is worth noting that, similarly to the earlier experiments on laboratory-grown ice (Murdza and others, Reference Murdza, Schulson and Renshaw2020), acoustic emissions were essentially not detected above minimum AE amplitude detection of 45 dB (unlike Langhorne and Haskell, Reference Langhorne and Haskell1996; Cole and Dempsey, (Reference Cole and Dempsey2004, Reference Cole and Dempsey2006); Lishman and others, Reference Lishman, Marchenko, Sammonds and Murdza2020) until the ice broke into two pieces and that the remnant pieces contained no cracks large enough to be detected by eye. This means that the flexural strength of both the lake ice and the lab ice was governed by the tensile stress to nucleate the first crack.
Not detected by the unaided eye in the present experiments were grain boundary decohesions (Ignat and Frost, Reference Ignat and Frost1987; b; Nickolayev and Schulson, Reference Nickolayev and Schulson1995, Picu and Gupta, Reference Picu and Gupta1995a; Gupta and others, Reference Gupta, Picu and Bergström1997; Weiss and Schulson, Reference Weiss and Schulson2000; Frost, Reference Frost2001). Features of that kind were quite prominent in earlier tests (Iliescu and others, Reference Iliescu, Murdza, Schulson and Renshaw2017; Murdza and others, Reference Murdza, Schulson and Renshaw2020) and were taken to be evidence of grain boundary sliding. That we did not observe them here does not necessarily mean that grain boundary sliding did not occur. Fewer grains boundaries appropriately oriented for sliding were located within the narrow region of highest tensile stress in 3-point bending (present case) and so this could account for the apparent absence of decohesions.
Discussion
Although the physical process underlying cyclic strengthening is not the focus of this letter, our sense is that the process is probably similar to the one discussed in Murdza and others (Reference Murdza, Schulson and Renshaw2020) for laboratory-grown ice; namely the development of an internal back-stress that opposes the applied stress in nucleating cracks. It may be significant that of the two possible mechanisms proposed earlier (Murdza and others, Reference Murdza, Schulson and Renshaw2020) for generating back-stress, namely dislocation pileups and grain boundary sliding, the latter may be the less likely, given that the strengthening measured in the present experiments is very close to that measured earlier, yet decohesions were not detected. However, given that under a 3-point bending much smaller volume of ice is subjected to the critical stress compared with a 4-point bending, there could be no grain boundaries that are favorably oriented for grain boundary sliding. Indeed, Figure 10 in Murdza and others (Reference Murdza, Schulson and Renshaw2020) shows that not all the boundaries are favorably oriented for decohesion development. Therefore, further work is required to elucidate the underlying physics.
Lastly, we would like to caution the reader to not necessarily expect the strengthening of every lake ice upon cycling; for example, in the case of lake ice with c-axis oriented vertically, no shear stress acts on basal planes when the ice cover is flexed and so the results can be different.
Conclusions
New results, although few in number, indicate that ice produced under natural conditions on an Arctic lake when flexed in the laboratory in a nonreversed manner under 3-point loading at −12 °C and 0.1 Hz, is strengthened upon cycling. In other words, cyclic strengthening appears to be a characteristic of ice per se and not of its origin nor of the exact method of cycling.
Acknowledgements
This work was supported by Research Council of Norway (RCN) and Norwegian Centre for International Cooperation in Higher Education (SIU) through the Arctic Offshore and Coastal Engineering in Changing Climate (AOCEC) project, no. 274951, 2018–2020. The work was also partially supported by the US Department of the Interior-Bureau of Safety and Environmental Enforcement (BSEE), contract no. E16PC00005. The authors wish to thank Prof. Alexander Sakharov, Dr Evgeny Karulin and Dr Petr Chistyakov for help in the preparation of experiments.







