Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Herbelin, Hugo
and
Ghilezan, Silvia
2008.
An approach to call-by-name delimited continuations.
p.
383.
Herbelin, Hugo
and
Ghilezan, Silvia
2008.
An approach to call-by-name delimited continuations.
ACM SIGPLAN Notices,
Vol. 43,
Issue. 1,
p.
383.
Ariola, Zena M.
Herbelin, Hugo
and
Sabry, Amr
2009.
A type-theoretic foundation of delimited continuations.
Higher-Order and Symbolic Computation,
Vol. 22,
Issue. 3,
p.
233.
Herbelin, Hugo
and
Zimmermann, Stéphane
2009.
Typed Lambda Calculi and Applications.
Vol. 5608,
Issue. ,
p.
142.
Ariola, Zena M.
Herbelin, Hugo
and
Saurin, Alexis
2011.
Typed Lambda Calculi and Applications.
Vol. 6690,
Issue. ,
p.
27.
Ariola, Zena M.
Downen, Paul
Herbelin, Hugo
Nakata, Keiko
and
Saurin, Alexis
2012.
Functional and Logic Programming.
Vol. 7294,
Issue. ,
p.
32.
Downen, Paul
and
Ariola, Zena M.
2012.
Programming Languages and Systems.
Vol. 7211,
Issue. ,
p.
234.
Geron, Bram
and
Geuvers, Herman
2013.
Continuation calculus.
Electronic Proceedings in Theoretical Computer Science,
Vol. 127,
Issue. ,
p.
66.
Downen, Paul
and
Ariola, Zena M.
2014.
Compositional semantics for composable continuations.
p.
109.
DOWNEN, PAUL
and
ARIOLA, ZENA M.
2014.
Delimited control and computational effects.
Journal of Functional Programming,
Vol. 24,
Issue. 1,
p.
1.
Munch-Maccagnoni, Guillaume
2014.
Formulae-as-types for an involutive negation.
p.
1.
Munch-Maccagnoni, Guillaume
2014.
Foundations of Software Science and Computation Structures.
Vol. 8412,
Issue. ,
p.
396.
Downen, Paul
and
Ariola, Zena M.
2014.
Compositional semantics for composable continuations.
ACM SIGPLAN Notices,
Vol. 49,
Issue. 9,
p.
109.
Downen, Paul
Maurer, Luke
Ariola, Zena M.
and
Peyton Jones, Simon
2016.
Sequent calculus as a compiler intermediate language.
ACM SIGPLAN Notices,
Vol. 51,
Issue. 9,
p.
74.
Downen, Paul
Maurer, Luke
Ariola, Zena M.
and
Peyton Jones, Simon
2016.
Sequent calculus as a compiler intermediate language.
p.
74.
Espírito Santo, José
and
Sousa, Ana Catarina
2026.
Logic, Language, Information, and Computation.
Vol. 15942,
Issue. ,
p.
293.
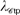 control calculus, developed by the authors, distinguishes between jumps and terms. This alternative calculus, which derives from Parigot's λμ-calculus, works by direct structural substitution of evaluation contexts. We review and revisit the legacy theories of control and argue that
control calculus, developed by the authors, distinguishes between jumps and terms. This alternative calculus, which derives from Parigot's λμ-calculus, works by direct structural substitution of evaluation contexts. We review and revisit the legacy theories of control and argue that 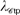 provides an observationally equivalent but smoother theory. In an additional note contributed by Matthias Felleisen, we review the story of the birth of control calculi during the mid- to late-eighties at Indiana University.
provides an observationally equivalent but smoother theory. In an additional note contributed by Matthias Felleisen, we review the story of the birth of control calculi during the mid- to late-eighties at Indiana University.

Discussions
No Discussions have been published for this article.