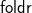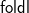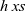Functional Pearls
Contents
Functional Pearl
Folding left and right matters: Direct style, accumulators, and continuations
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 33 / 2023
- Published online by Cambridge University Press:
- 14 February 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Knuth–Morris–Pratt illustrated
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 34 / 2024
- Published online by Cambridge University Press:
- 30 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An optimal, purely functional implementation of the Garsia–Wachs algorithm
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 30 / 2020
- Published online by Cambridge University Press:
- 21 January 2020, e3
-
- Article
-
- You have access
- Export citation
You could have invented Fenwick trees
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 35 / 2025
- Published online by Cambridge University Press:
- 17 January 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How to mingle streams
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 25 / 2015
- Published online by Cambridge University Press:
- 16 March 2015, e4
-
- Article
-
- You have access
- Export citation
Super-naturals
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 32 / 2022
- Published online by Cambridge University Press:
- 31 January 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turner, Bird, Eratosthenes: An eternal burning thread
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 35 / 2025
- Published online by Cambridge University Press:
- 05 February 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Folding left and right over Peano numbers
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 29 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, e6
-
- Article
-
- You have access
- Export citation
How much is in a square? Calculating functional programs with squares
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 35 / 2025
- Published online by Cambridge University Press:
- 26 February 2025, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Many more predecessors: A representation workout
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 30 / 2020
- Published online by Cambridge University Press:
- 30 March 2020, e7
-
- Article
-
- You have access
- Export citation
How to find a fake coin
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 29 / 2019
- Published online by Cambridge University Press:
- 29 April 2019, e8
-
- Article
-
- You have access
- Export citation
Binary search—think positive
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 35 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A well-known representation of monoids and its application to the function ‘vector reverse’
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 32 / 2022
- Published online by Cambridge University Press:
- 08 August 2022, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Heterogeneous binary random-access lists
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 30 / 2020
- Published online by Cambridge University Press:
- 07 April 2020, e10
-
- Article
-
- You have access
- Open access
- Export citation
A correct-by-construction conversion from lambda calculus to combinatory logic
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 33 / 2023
- Published online by Cambridge University Press:
- 22 November 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Certified, total serialisers with an application to Huffman encoding
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 33 / 2023
- Published online by Cambridge University Press:
- 12 December 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Composable data visualizations
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 31 / 2021
- Published online by Cambridge University Press:
- 17 June 2021, e13
-
- Article
-
- You have access
- Open access
- Export citation
Batcher's odd-even merging network revealed
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 28 / 2018
- Published online by Cambridge University Press:
- 04 June 2018, e14
-
- Article
-
- You have access
- Export citation
Bottom-up computation using trees of sublists
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 34 / 2024
- Published online by Cambridge University Press:
- 11 December 2024, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On constructing 2-3 trees
- Part of:
-
- Journal:
- Journal of Functional Programming / Volume 28 / 2018
- Published online by Cambridge University Press:
- 26 October 2018, e19
-
- Article
-
- You have access
- Export citation