Published online by Cambridge University Press: 06 January 2022
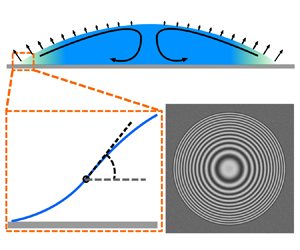
New light is shed on morphological features of water–propylene glycol sessile droplets evaporating into ambient air at not too high relative humidity. Such droplets adopt a Marangoni-contracted shape even on perfectly wetting substrates, an effect well known since Cira et al. (Nature, 519, 2015). We here highlight a strong separation of scales normally occurring for such droplets. Namely, there is a narrow high-curvature zone localized at the foot of the droplet, where the apparent contact angle is formed, while the core of the droplet merely adheres to the classical (capillary–gravity) static shape. Experimentally, we rely upon interferometry to discern such fine key details. We detect a maximum of the droplet slope profile in the foot region, which amounts to the apparent contact angle. Theoretically, a local description of the foot region is devised. We indicate a crucial role of convective mixing by the solutal Marangoni flow, here accounted for by the Taylor dispersion, which proves to underlie the separation of scales and ensure self-consistency of the local model. Migration of such droplets in a humidity gradient is also approached within the same experimental and theoretical framework. It is considered that the resulting back–front asymmetry of the apparent contact angles drives the motion similarly to a wettability gradient, although the drag (‘Cox–Voinov’) factor is here found to be different. The predictions, comparing well with the measurements (our own and from the literature), are based on rigorous models, isothermal and as reduced as possible, without any fitting parameters or microphysics effects.