Article contents
Wall skin friction analysis in a hypersonic turbulent boundary layer over a compression ramp
Published online by Cambridge University Press: 31 May 2024
Abstract
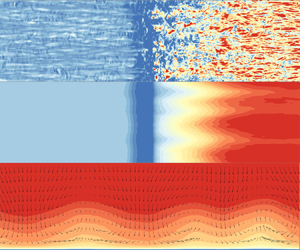
In this paper, direct numerical simulations in hypersonic turbulent boundary layers over a  $24^{\circ }$ compression ramp at Mach 6.0 are performed. The wall skin friction and its spanwise non-homogeneity in the interaction region are analysed via the spectral analysis and drag decomposition method. On the compression ramp, the premultiplied spanwise energy spectrum of wall shear stress
$24^{\circ }$ compression ramp at Mach 6.0 are performed. The wall skin friction and its spanwise non-homogeneity in the interaction region are analysed via the spectral analysis and drag decomposition method. On the compression ramp, the premultiplied spanwise energy spectrum of wall shear stress  $\tau _{w}$ reveals two energetic spanwise length scales. One occurs in the region of
$\tau _{w}$ reveals two energetic spanwise length scales. One occurs in the region of  $x/\delta _{ref}=0\unicode{x2013}3$ (
$x/\delta _{ref}=0\unicode{x2013}3$ ( $x=0$ lies in the compression corner;
$x=0$ lies in the compression corner;  $\delta _{ref}$ is the boundary layer thickness upstream of the interaction region) and is consistent with that of the large-scale streamwise vortices, indicating that the fluctuation intensity of
$\delta _{ref}$ is the boundary layer thickness upstream of the interaction region) and is consistent with that of the large-scale streamwise vortices, indicating that the fluctuation intensity of  $\tau _{w}$ is associated with the Görtler-type structures. The other one is observed downstream of
$\tau _{w}$ is associated with the Görtler-type structures. The other one is observed downstream of  $x/\delta _{ref}=3.0$ and corresponds to the regenerated elongated streaky structures. The fluctuation intensity of
$x/\delta _{ref}=3.0$ and corresponds to the regenerated elongated streaky structures. The fluctuation intensity of  $\tau _{w}$ peaks at
$\tau _{w}$ peaks at  $x/\delta _{ref}=3.0$, where both the above energetic length scales are observed. The drag decomposition method proposed by Li et al. (J. Fluid Mech., vol. 875, 2019, pp. 101–123) is extended to include the effects of spanwise non-homogeneity so that it can be used in the interaction region where the mean flow field and the mean skin friction
$x/\delta _{ref}=3.0$, where both the above energetic length scales are observed. The drag decomposition method proposed by Li et al. (J. Fluid Mech., vol. 875, 2019, pp. 101–123) is extended to include the effects of spanwise non-homogeneity so that it can be used in the interaction region where the mean flow field and the mean skin friction  $C_f$ exhibit an obvious spanwise heterogeneity. The results reveal that, in the upstream turbulent boundary layer, the drag contribution arising from the spanwise heterogeneity can be neglected, while this value on the compression ramp is up to 20.7 % of
$C_f$ exhibit an obvious spanwise heterogeneity. The results reveal that, in the upstream turbulent boundary layer, the drag contribution arising from the spanwise heterogeneity can be neglected, while this value on the compression ramp is up to 20.7 % of  $C_f$, resulting from the Görtler-type vortices. With the aid of the drag decomposition method, it is found that the main flow features that contribute positively to the amplification of
$C_f$, resulting from the Görtler-type vortices. With the aid of the drag decomposition method, it is found that the main flow features that contribute positively to the amplification of  $C_f$ and its rapid increase on the compression ramp includes: the density increase across the shock, the high mean shear stress and turbulence amplification around the detached shear layer and the Favre-averaged downward velocity towards the ramp wall. Compared with the spanwise-averaged value,
$C_f$ and its rapid increase on the compression ramp includes: the density increase across the shock, the high mean shear stress and turbulence amplification around the detached shear layer and the Favre-averaged downward velocity towards the ramp wall. Compared with the spanwise-averaged value,  $C_f$ and its components at the spanwise station where the downwash and upwash of the Görtler-type vortices occur reveal a spanwise variation exceeding 10 %.
$C_f$ and its components at the spanwise station where the downwash and upwash of the Görtler-type vortices occur reveal a spanwise variation exceeding 10 %.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 8
- Cited by


