Article contents
Wall friction and velocity measurements in a double-frequency pulsating turbulent flow
Published online by Cambridge University Press: 08 January 2016
Abstract
Wall shear stress measurements employing a hot-film sensor along with laser Doppler velocimetry measurements of the axial and tangential velocity and turbulence profiles in a pulsating turbulent pipe flow are presented. Time-mean and phase-averaged results are derived from measurements performed at pulsation frequencies 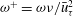 ${\it\omega}^{+}={\it\omega}{\it\nu}/\bar{u}_{{\it\tau}}^{2}$ over the range of 0.003–0.03, covering the low-frequency, intermediate and quasi-laminar regimes. In addition to the base case of a single pulsation imposed on the mean flow, the study also investigates the flow response when two pulsations are superimposed simultaneously. The measurements from the base case show that, when the pulsation belongs to the quasi-laminar regime, the oscillating flow tends towards a laminar state in which the velocity approaches the purely viscous Stokes solution with a low level of turbulence. For
${\it\omega}^{+}={\it\omega}{\it\nu}/\bar{u}_{{\it\tau}}^{2}$ over the range of 0.003–0.03, covering the low-frequency, intermediate and quasi-laminar regimes. In addition to the base case of a single pulsation imposed on the mean flow, the study also investigates the flow response when two pulsations are superimposed simultaneously. The measurements from the base case show that, when the pulsation belongs to the quasi-laminar regime, the oscillating flow tends towards a laminar state in which the velocity approaches the purely viscous Stokes solution with a low level of turbulence. For 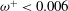 ${\it\omega}^{+}<0.006$ , the oscillating flow is turbulent and exhibits a region with a logarithmic velocity distribution and a collapse of the turbulence intensities, similar to the time-averaged counterparts. In the low-frequency regime, the oscillating wall shear stress is shown to be directly proportional to the Stokes length normalized in wall units
${\it\omega}^{+}<0.006$ , the oscillating flow is turbulent and exhibits a region with a logarithmic velocity distribution and a collapse of the turbulence intensities, similar to the time-averaged counterparts. In the low-frequency regime, the oscillating wall shear stress is shown to be directly proportional to the Stokes length normalized in wall units 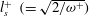 $l_{s}^{+}~(=\sqrt{2/{\it\omega}^{+}})$ , as predicted by quasi-steady theory. The base case measurements are used as a reference when evaluating the data from the double-frequency case and the oscillating quantities are shown to be close to superpositions from the base case. The previously established view that the time-averaged quantities are unaffected by the imposition of small-amplitude pulsed unsteadiness is shown to hold also when two pulsations are superposed on the mean flow.
$l_{s}^{+}~(=\sqrt{2/{\it\omega}^{+}})$ , as predicted by quasi-steady theory. The base case measurements are used as a reference when evaluating the data from the double-frequency case and the oscillating quantities are shown to be close to superpositions from the base case. The previously established view that the time-averaged quantities are unaffected by the imposition of small-amplitude pulsed unsteadiness is shown to hold also when two pulsations are superposed on the mean flow.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 6
- Cited by


