Article contents
Vortical–acoustic resonance in an acoustic resonator: Strouhal number variation, destabilization and stabilization
Published online by Cambridge University Press: 26 May 2021
Abstract
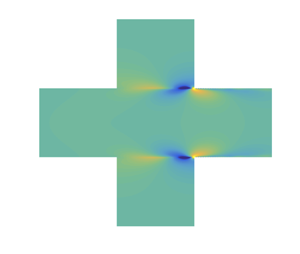
The impact of acoustic resonance on vortical–acoustic resonance and flow instability is studied by a combined travelling–global mode analysis about a low-speed inviscid parallel shear flow in two-dimensional symmetric duct–cavity configurations. First, in a shallow-cavity case, we show that the difference between incompressible and compressible models in describing the compact feedback loop, consisting of the Kelvin–Helmholtz (KH) instability wave and the Rayleigh–Powell–Rossiter (RPR) feedback, is small and the global mode frequency follows the Strouhal law. Using the compact case as a baseline for comparison, the influence of an acoustic resonator (AR) on the  $\textrm {KH}+\textrm {RPR}$ feedback loop is then examined. In this deep-cavity case, phenomena such as frequency deviation from the Strouhal law, global mode switching, global mode destabilization and stabilization, caused by a trapped or a heavily damped acoustic resonant mode, are observed. We show that those phenomena can be explained by the local–global relation of the feedback loop and the dual-feedback view: the coexistence of RPR and AR feedbacks. The Strouhal number variation is due to the phase difference of the unstable vortical wave between the upstream and downstream cavity edges being changed by the additional AR feedback. It is found that the switching is not a vortical but an acoustic effect. The destabilization and stabilization, near and far from an acoustic resonance, are respectively understood as the result of the total feedback at the upstream edge being strengthened and weakened by the AR feedback.
$\textrm {KH}+\textrm {RPR}$ feedback loop is then examined. In this deep-cavity case, phenomena such as frequency deviation from the Strouhal law, global mode switching, global mode destabilization and stabilization, caused by a trapped or a heavily damped acoustic resonant mode, are observed. We show that those phenomena can be explained by the local–global relation of the feedback loop and the dual-feedback view: the coexistence of RPR and AR feedbacks. The Strouhal number variation is due to the phase difference of the unstable vortical wave between the upstream and downstream cavity edges being changed by the additional AR feedback. It is found that the switching is not a vortical but an acoustic effect. The destabilization and stabilization, near and far from an acoustic resonance, are respectively understood as the result of the total feedback at the upstream edge being strengthened and weakened by the AR feedback.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 4
- Cited by


