Article contents
Vortex separation and interaction in the wake of inclined trapezoidal plates
Published online by Cambridge University Press: 20 April 2015
Abstract
Full three-dimensional numerical simulations are employed to investigate the flows over inclined trapezoidal low-aspect-ratio plates at low Reynolds numbers, aiming to understand the unsteadiness induced by the interaction between the trailing vortical wake structures originating from the swept edges, and those from the leading and trailing edges. The flows past eighteen different plate geometries in three broad sets are simulated to study the influence of aspect ratio, taper angle and angle of attack on the wake vortices and the force coefficients. Both taper ratio and angle of attack of plates with the same area are found to have a broadly predictable influence on the wake stability and asymptotic forces. Smaller taper ratios result in lower maximum lift, while an increase in the angle of attack results in a reduction in the differences in maximum lift. Two distinct modes of periodic unsteady flow with significant differences in frequency are observed. The corresponding vortex-shedding mechanisms are analysed with the aid of 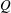 $Q$ -criterion isosurfaces and streamlines. A low wake frequency is observed at small taper angles when there is relative independence between the von Kármán vortices originating from the leading and trailing edges, and weak swept-edge vortices. The dominant Strouhal number in this state is approximately 0.09. When the taper angle or angle of attack increases, the flows over the swept edges form stronger trailing vortex structures which interact strongly with the leading-edge vortices, combining to produce a regular stream of vortex loops shed into the wake. In this regime, the dominant Strouhal number increases to approximately 0.14–0.18. Higher Reynolds numbers and/or angles of attack result in a loss of centre plane reflection symmetry in the wake. The aerodynamic forces have been quantified as a function of the problem parameters and plate geometry.
$Q$ -criterion isosurfaces and streamlines. A low wake frequency is observed at small taper angles when there is relative independence between the von Kármán vortices originating from the leading and trailing edges, and weak swept-edge vortices. The dominant Strouhal number in this state is approximately 0.09. When the taper angle or angle of attack increases, the flows over the swept edges form stronger trailing vortex structures which interact strongly with the leading-edge vortices, combining to produce a regular stream of vortex loops shed into the wake. In this regime, the dominant Strouhal number increases to approximately 0.14–0.18. Higher Reynolds numbers and/or angles of attack result in a loss of centre plane reflection symmetry in the wake. The aerodynamic forces have been quantified as a function of the problem parameters and plate geometry.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 10
- Cited by


