Article contents
Vortex impingement onto an axisymmetric obstacle – subcritical bifurcation to vortex breakdown
Published online by Cambridge University Press: 15 January 2021
Abstract
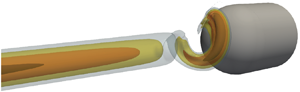
A swirling wake flow submitted to an adverse pressure gradient is studied by bifurcation analysis, modal analysis and direct numerical simulations. In contrast to experiments in diverging tubes, the adverse pressure gradient is imposed by the presence of a downstream axisymmetric obstacle centred on the vortex axis. Different adverse pressure gradients are investigated by modifying the obstacle radius, which results in the deceleration of the vortex axial velocity. Hence, vortex breakdown occurs for a sufficiently large pressure gradient. We observe a spiral vortex breakdown type without any recirculation bubble, which contrasts with classical spiral vortex breakdown developing in the bubble wake. A weakly nonlinear analysis is performed to characterize this self-sustained instability. The resulting Landau equation reveals the sub-critical character of this Hopf bifurcation, highlighting a sub-critical vortex breakdown. In addition, the stabilization mechanism of this spiral vortex breakdown caused by an off-centre displacement of the downstream axisymmetric obstacle is investigated by direct numerical simulations. Nonlinear dynamics, such as a quasi-periodic state, is observed as a consequence of nonlinear interactions between the spiral vortex breakdown and the misalignment of the obstacle before the stabilization occurs.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 4
- Cited by


