Article contents
Visualization of the Ludford column
Published online by Cambridge University Press: 13 March 2013
Abstract
When a liquid metal flows around a truncated cylinder in the presence of a magnetic field which is parallel to the axis of the cylinder, a stagnant region develops above the cylinder. We call this region a Ludford column. The Ludford column represents the magnetohydrodynamics (MHD) analogue of the well-known Taylor columns in rotating flows. Whereas Taylor columns can be easily visualized using dye, the visualization of Ludford columns has remained elusive up to now because liquid metals are opaque. We demonstrate that this fundamental limitation of experimental MHD can be overcome by using a superconducting 5 T magnet. This facility permits us to perform MHD experiments in which the opaque liquid metals are replaced with a transparent electrolyte while maintaining the key MHD effects. We report results of a series of flow experiments in which an aqueous solution of sulphuric acid flows around a bar with square cross-section (which for simplicity shall be referred to as a cylinder). We vary the Reynolds number in the range 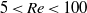 $5\lt Re\lt 100$ and the Hartmann number in the range
$5\lt Re\lt 100$ and the Hartmann number in the range 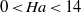 $0\lt Ha\lt 14$ . The experimental procedure involves flow visualizations using tracer particles as well as velocity measurements using particle image velocimetry (PIV). Our experiments provide direct access to the Ludford column for the first time and reveal the spatial structure of this basic feature of MHD flows.
$0\lt Ha\lt 14$ . The experimental procedure involves flow visualizations using tracer particles as well as velocity measurements using particle image velocimetry (PIV). Our experiments provide direct access to the Ludford column for the first time and reveal the spatial structure of this basic feature of MHD flows.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
Footnotes
Present address: Institute of Fluid Dynamics, Helmholtz-Zentrum Dresden-Rossendorf, Bautzner Landstraße 400, 01328 Dresden, Germany.
References
- 12
- Cited by

