Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T22:04:50.544Z Has data issue: false hasContentIssue false
  • English
  • Français

Very large scale motions in the atmospheric surface layer: a field investigation

Published online by Cambridge University Press:  04 August 2016

Guohua Wang  and
Xiaojing Zheng
Guohua Wang
Affiliation:
Key Laboratory of Mechanics on Disaster and Environment in Western China, The Ministry of Education of China, Department of Mechanics, Lanzhou University, Lanzhou 730000, PR China
Xiaojing Zheng*
Affiliation:
Research Center for Applied Mechanics, School of Mechano-Electronic Engineering, Xidian University, Xi’an 710071, PR China
*
†Email address for correspondence: xjzheng@xidian.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A field observation array for the atmospheric surface layer (ASL) was built on a dry flat bed of Qingtu Lake in Minqin (China) as the Qingtu Lake Observation Array (QLOA) site, which is similar to the Surface Layer Turbulence and Environmental Science Test (SLTEST) site in the Utah (USA) Western desert. The present observation array can synchronously perform multi-point measurements of wind velocity and temperature at different vertical and streamwise positions. 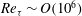In other words, three-dimensional turbulent ASL flows can be measured at the QLOA station and Reynolds numbers as high as $Re_{\unicode[STIX]{x1D70F}}\sim O(10^{6})$ can be achieved with steady wind conditions. By careful selection and pretreatment for measured data of more than 1200 h, the QLOA data have been validated to be reliable for high Reynolds number turbulent boundary layer research. Results from correlation and spectral analysis confirm that very large scale motions (VLSMs) exist in the ASL at a Reynolds number up to $Re_{\unicode[STIX]{x1D70F}}\approx 4\times 10^{6}$ . Through premultiplied spectral analysis, it is revealed that the spectral energy in the high-wavenumber region decreases with height, similar to turbulent boundary layers at low or moderate Reynolds numbers, while it increases with height in the low-wavenumber region resulting in a log–linear increase of VLSMs energy with height, which is different from turbulent boundary layers at low or moderate Reynolds numbers. The present analyses support the view that the evolution of the VLSMs cannot be fully attributed to a ‘bottom-up’ mechanism alone, and probably other mechanisms, including a ‘top-down’ mechanism, also play a role.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Boundary Layers: Boundary layer structure

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 464 - 489
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
del Alamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
Bailey, S. C. C. & Smits, A. J. 2010 Experimental investigation of the structure of large- and very large-scale motions in turbulent pipe flow. J. Fluid Mech. 651, 339–356.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large-and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google ScholarPubMed
Balasubramaniam, B. J.2005 Nature of turbulence in wall-bounded flows. PhD Thesis, University of Illinois at Urbana-Champaign.Google Scholar
Camp, D. W. & Kaufman, J. W. 1970 Comparison of tower influence on wind velocity for nasa’s 150-meter meteorological tower and a wind tunnel model of the tower. J. Geophys. Res. 75 (6), 1117–1121.CrossRefGoogle Scholar
Chauhan, K. A.2007 Study of canonical wall-bounded turbulent flows. PhD thesis, Illinois Institute of Technology.Google Scholar
Chin, C., Monty, J. P. & Ooi, A. 2014 Reynolds number effects in dns of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.CrossRefGoogle Scholar
Chung, D., Marusic, I., Monty, J. P., Vallikivi, M. & Smits, A. J. 2015 On the universality of inertial energy in the log layer of turbulent boundary layer and pipe flows. Exp. Fluids 56 (7), 141.CrossRefGoogle Scholar
Clauser, F. H. 1956 The turbulent boundary layer. Adv. Appl. Mech. 4, 1–51.CrossRefGoogle Scholar
Cooper, D. I., Leclerc, M. Y., Archuleta, J., Coulter, R., Eichinger, W. E., Kao, C. Y. J. & Nappo, C. J. 2006 Mass exchange in the stable boundary layer by coherent structures. Agric. Forest Meteorol. 136 (3), 114–131.Google Scholar
Dabberdt, W. F. 1968 Wind disturbance by a vertical cylinder in the atmospheric surface layer. J. Appl. Meteorol. 7 (3), 367–371.Google Scholar
Foken, T., Göockede, M., Mauder, M., Mahrt, L., Amiro, B. & Munger, W. 2004 Post-field data quality control. In Handbook of Micrometeorology, pp. 181–208. Springer.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.CrossRefGoogle Scholar
Graaff, D. B. De & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2011 Interactions within the turbulent boundary layer at high Reynolds number. J. Fluid Mech. 666, 573–604.Google Scholar
Högström, U., Hunt, J. C. R. & Smedman, A. S. 2002 Theory and measurements for turbulence spectra and variances in the atmospheric neutral surface layer. Boundary-Layer Meteorol. 103, 101–124.Google Scholar
Hommema, S. E. & Adrian, R. J. 2003 Packet structure of surface eddies in the atmospheric boundary layer. Boundary Layer Meteorol. 106 (1), 147–170.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, 094501.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Hunt, J. C. R. & Morrison, J. F. 2000 Eddy structure in turbulent boundary layers. Eur. J. Mech. (B/Fluids) 19 (5), 673–694.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary Layer Meteorol. 145 (2), 273–306.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google ScholarPubMed
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Klewicki, J. C., Metzger, M. M., Kelner, E. & Thurlow, E. M. 1995 Viscous sublayer flow visualizations at R𝜃 ≃ 1 500 000. Phys. Fluids 7 (4), 857–863.Google Scholar
Knobloch, K. & Fernholz, H. H. 2004 Statistics, correlations, and scaling in a turbulent boundary layer at Re 𝛿2⩽1. 15 × 105 . In IUTAM Symposium on Reynolds Number Scaling in Turbulent Flow, pp. 11–16. Springer.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41 (02), 283–325.Google Scholar
Kulandaivelu, V. & Marusic, I. 2010 Evolution of zero pressure gradient turbulent boundary layers. In Proceedings of the 17th Australasian Fluid Mechanics Conference, Paper 196, Auckland.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Lee, J., Ahn, J. & Sung, H. J. 2015 Comparison of large- and very-large-scale motions in turbulent pipe and channel flows. Phys. Fluids 27, 025101.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25, 045103.CrossRefGoogle Scholar
Ligrani, P. M. & Moffat, R. J. 1986 Structure of transitionally rough and fully rough turbulent boundary layers. J. Fluid Mech. 162, 69–98.Google Scholar
Marusic, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.CrossRefGoogle ScholarPubMed
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Metzger, M., McKeon, B. J. & Holmes, H. 2007 The near-neutral atmospheric surface layer: turbulence and non-stationarity. Phil. Trans. R. Soc. Lond. A 365, 859–876.Google Scholar
Metzger, M. M. 2006 Length and time scales of the near-surface axial velocity in a high Reynolds number turbulent boundary layer. Intl J. Heat Fluid Flow 27 (4), 534–541.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13 (3), 692–701.Google Scholar
Metzger, M. M., Klewicki, J. C., Bradshaw, K. L. & Sadr, R. 2001 Scaling the near-wall axial turbulent stress in the zero pressure gradient boundary layer. Phys. Fluids 13 (6), 1819–1821.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Morrison, J. F. 2007 The interaction between inner and outer regions of turbulent wall-bounded flow. Phil. Trans. R. Soc. Lond. A 365 (1852), 683–698.Google Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20 (10), 1518.Google Scholar
Ong, L. & Wallace, J. 1996 The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 20 (6), 441–453.CrossRefGoogle Scholar
Österlund, J. M., Johansson, A. V., Nagib, H. M. & Hites, M. H. 2000 A note on the overlap region in turbulent boundary layers. Phys. Fluids 12 (1), 1–4.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth-and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.CrossRefGoogle Scholar
Sauermann, G., Kroy, K. & Herrmann, H. J. 2001 Continuum saltation model for sand dunes. Phys. Rev. E 64 (3), 031305.Google Scholar
Schoppa, W. & Hussain, F. 1997 Genesis and dynamics of coherent structures in near-wall turbulence – a new look. In Self-Sustaining Mechanisms of Wall Turbulence, pp. 385–442. Computational Mechanics Publications.Google Scholar
Serafimovich, A., Thomas, C. & Foken, T. 2011 Vertical and horizontal transport of energy and matter by coherent motions in a tall spruce canopy. Boundary Layer Meteorol. 140 (3), 429–451.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Stull, R. B. 1988 An Introduction to Boundary Layer Meteorology. Kluwer.Google Scholar
Talamelli, A., Persiani, F., Fransson, J. H. M., Alfredsson, P. H., Johansson, A. V., Nagib, H. M., Rüedi, J. D., Sreenivasan, K. R. & Monkewitz, P. A. 2009 Ciclopea response to the need for high Reynolds number experiments. Fluid Dyn. Res. 41 (2), 021407.CrossRefGoogle Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. 164 (919), 476–490.Google Scholar
Vallikivi, M.2014 Wall-bounded turbulence at high Reynolds numbers. PhD thesis, Princeton University.Google Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015a Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.CrossRefGoogle Scholar
Vallikivi, M., Hultmark, M. & Smits, A. J. 2015b Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.Google Scholar
Vincenti, P., Klewicki, J., Morrill-Winter, C., White, C. M. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp. Fluids 54, 1629.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.Google Scholar
Zhao, R. & Smits, A. J. 2007 Scaling of the wall-normal turbulence component in high-Reynolds-number pipe flow. J. Fluid Mech. 576, 457–473.Google Scholar
Zheng, X. J., Zhang, J. H., Wang, G. H., Liu, H. Y. & Zhu, W. 2013 Investigation on very large scale motions (VLSMs) and their influence in a dust storm. Sci. China-Phys. Mech. Astron. 56, 306–314.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar