Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sasidharan, Vaisakh
and
Duvvuri, Subrahmanyam
2021.
Large- and small-amplitude shock-wave oscillations over axisymmetric bodies in high-speed flow.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Hao, Jiaao
Fan, Jianhui
Cao, Shibin
and
Wen, Chih-Yung
2022.
Three-dimensionality of hypersonic laminar flow over a double cone.
Journal of Fluid Mechanics,
Vol. 935,
Issue. ,
Hong, Qizhen
Hao, Jiaao
Uy, Ken Chun Kit
Wen, Chih-Yung
and
Sun, Quanhua
2022.
Thermochemical nonequilibrium effects on high-enthalpy double-wedge flows.
Physics of Fluids,
Vol. 34,
Issue. 6,
Fan, Jianhui
Hao, Jiaao
and
Wen, Chih-Yung
2022.
Nonlinear interactions of global instabilities in hypersonic laminar flow over a double cone.
Physics of Fluids,
Vol. 34,
Issue. 12,
Karpuzcu, Irmak Taylan
Levin, Deborah A.
Cerulus, Nicolas
and
Theofilis, Vassilios
2022.
On Linear Stability of Compression Corner Flows Obtained by Kinetic Theory.
Karpuzcu, Irmak Taylan
Levin, Deborah A.
Cerulus, Nicolas
and
Theofilis, Vassilios
2023.
On the Unsteadiness and Three Dimensionality of a Laminar Separation Bubble for a Supersonic Flow over a Compression Corner.
Tumuklu, Ozgur
and
Hanquist, Kyle M.
2023.
Temporal characteristics of hypersonic flows over a double wedge with Reynolds number.
Physics of Fluids,
Vol. 35,
Issue. 10,
Duvvuri, Subrahmanyam
Kumar, Gaurav
and
Sasidharan, Vaisakh
2023.
On shock-wave unsteadiness in separated flows.
Sādhanā,
Vol. 48,
Issue. 3,
Karpuzcu, Irmak Taylan
Levin, Deborah A.
and
Theofilis, Vassilios
2023.
On the Unsteadiness of a Hypersonic Flow over a Double Cone using Kinetic Methods.
Karpuzcu, Irmak Taylan
Levin, Deborah A.
and
Theofilis, Vassilios
2023.
On the Unsteadiness of a Hypersonic Flow over an Axisymmetric Double Cone using Kinetic Methods.
Gibbons, Nicholas N.
Damm, Kyle A.
Jacobs, Peter A.
and
Gollan, Rowan J.
2023.
Eilmer: An open-source multi-physics hypersonic flow solver.
Computer Physics Communications,
Vol. 282,
Issue. ,
p.
108551.
Kumar, Gaurav
Sasidharan, Vaisakh
Kumara, Akshaya G.
and
Duvvuri, Subrahmanyam
2024.
A model for frequency scaling of flow oscillations in high-speed double cones.
Journal of Fluid Mechanics,
Vol. 988,
Issue. ,
Zhao, Guoqin
Ma, Tianju
Chen, Zongnan
Zhang, Zijian
Hao, Jiaao
and
Wen, Chih-Yung
2024.
Investigation of streamwise streak characteristics over a compression ramp at Mach 4.
Physics of Fluids,
Vol. 36,
Issue. 10,
Karpuzcu, Irmak T.
Levin, Deborah A.
and
Theofilis, Vassilis
2024.
On unsteadiness of hypersonic flow over a double cone.
Vol. 3050,
Issue. ,
p.
080021.
Ai, Junding
Huang, Wei
Zhang, Jincheng
and
Liu, Chaoyang
2024.
Study on the flow characteristics of double-cone in hypersonic flows.
Aerospace Science and Technology,
Vol. 155,
Issue. ,
p.
109645.
Acosta, Alex R.
Davis, Branson W.
Austin, Joanna M.
and
Hornung, Hans G.
2025.
Proceedings of the 34th International Symposium on Shock Waves, Volume 1: Fundamentals.
p.
239.
Ray, Anurag Adityanarayan
and
De, Ashoke
2025.
Influence of Reynolds number on the modes of unsteadiness on the double-wedge configurations.
Physics of Fluids,
Vol. 37,
Issue. 8,
LI, Cheng
and
HAO, Jiaao
2025.
Three-dimensional effects on establishment of hypersonic double-cone flow.
Chinese Journal of Aeronautics,
Vol. 38,
Issue. 12,
p.
103583.
XIE 谢, Wei 玮
LUO 罗, Zhenbing 振兵
ZHOU 周, Yan 岩
LIU 刘, Qiang 强
DENG 邓, Xiong 雄
and
ZHU 朱, Yinxin 寅鑫
2025.
Experimental and numerical study on double wedge shock/shock interaction controlled by a single-pulse plasma synthetic jet
.
Plasma Science and Technology,
Vol. 27,
Issue. 4,
p.
044004.
Li, Sijia
Guo, Jinghui
Zhang, Qiming
Ma, Xinyang
and
Lai, Jingsong
2025.
High-enthalpy unsteady pulsation flow over a double wedge.
Physics of Fluids,
Vol. 37,
Issue. 2,
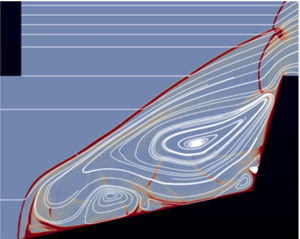
 $\theta _1$, and large second-cone angle,
$\theta _1$, and large second-cone angle,  $\theta _2$), is shown to be inviscid in nature. In
$\theta _2$), is shown to be inviscid in nature. In  $\theta _1$–
$\theta _1$– $\theta _2$ space, the region of unsteady flow is enclosed in a loop with a lower and an upper
$\theta _2$ space, the region of unsteady flow is enclosed in a loop with a lower and an upper  $\theta _2$ branch with a maximum
$\theta _2$ branch with a maximum  $\theta _1$ between. The location of the lower
$\theta _1$ between. The location of the lower  $\theta _2$ branch is determined by the second-cone detachment angle
$\theta _2$ branch is determined by the second-cone detachment angle  $\theta _{2d}$. For this reason, the gas model in one of the conditions is chosen to be thermally perfect carbon dioxide (at Mach number 8) for which
$\theta _{2d}$. For this reason, the gas model in one of the conditions is chosen to be thermally perfect carbon dioxide (at Mach number 8) for which  $\theta _{2d}$ is quite large. In the other cases, the gas model is perfect-gas nitrogen at Mach numbers 2, 4 and 7.7. In the hypersonic range, within the uncertainties, and in the parameter range covered, the unsteadiness boundary is shown to depend on only three dimensionless parameters.
$\theta _{2d}$ is quite large. In the other cases, the gas model is perfect-gas nitrogen at Mach numbers 2, 4 and 7.7. In the hypersonic range, within the uncertainties, and in the parameter range covered, the unsteadiness boundary is shown to depend on only three dimensionless parameters.

