Published online by Cambridge University Press: 26 April 2021
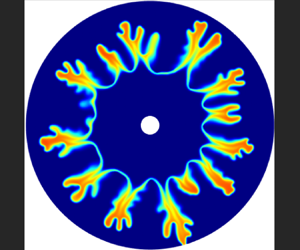
The effects of the  $A + B \rightarrow C$ chemical reaction on miscible viscous fingering in a radial source flow are analysed using linear stability theory and numerical simulations. This flow and transport problem is described by a system of nonlinear partial differential equations consisting of Darcy's law for an incompressible fluid coupled with nonlinear advection–diffusion–reaction equations. For an infinitely large Péclet number (
$A + B \rightarrow C$ chemical reaction on miscible viscous fingering in a radial source flow are analysed using linear stability theory and numerical simulations. This flow and transport problem is described by a system of nonlinear partial differential equations consisting of Darcy's law for an incompressible fluid coupled with nonlinear advection–diffusion–reaction equations. For an infinitely large Péclet number ( $Pe$), the linear stability equations are solved using spectral analysis. Further, the numerical shooting method is used to solve the linearized equations for various values of
$Pe$), the linear stability equations are solved using spectral analysis. Further, the numerical shooting method is used to solve the linearized equations for various values of  $Pe$ including the limit
$Pe$ including the limit  $Pe \rightarrow \infty$. In the linear analysis, we aim to capture various critical parameters for the instability using the concept of asymptotic instability, i.e. in the limit
$Pe \rightarrow \infty$. In the linear analysis, we aim to capture various critical parameters for the instability using the concept of asymptotic instability, i.e. in the limit  $\tau \rightarrow \infty$, where
$\tau \rightarrow \infty$, where  $\tau$ represents the dimensionless time. We restrict our analysis to the asymptotic limit
$\tau$ represents the dimensionless time. We restrict our analysis to the asymptotic limit  $Da^{\ast }$
$Da^{\ast }$ $(= Da \tau ) \rightarrow \infty$ and compare the results with the non-reactive case (
$(= Da \tau ) \rightarrow \infty$ and compare the results with the non-reactive case ( $Da = 0$) for which
$Da = 0$) for which  $Da^{\ast } = 0$, where
$Da^{\ast } = 0$, where  $Da$ is the Damköhler number. In the latter case, the dynamics is controlled by the dimensionless parameter
$Da$ is the Damköhler number. In the latter case, the dynamics is controlled by the dimensionless parameter  $R_{Phys} = -(R_{A} - \beta R_{B})$. In the former case, for a fixed value of
$R_{Phys} = -(R_{A} - \beta R_{B})$. In the former case, for a fixed value of  $R_{Phys}$, the dynamics is determined by the dimensionless parameter
$R_{Phys}$, the dynamics is determined by the dimensionless parameter  $R_{Chem} = -(R_{C} - R_{B} - R_{A})$. Here,
$R_{Chem} = -(R_{C} - R_{B} - R_{A})$. Here,  $\beta$ is the ratio of reactants’ initial concentration and
$\beta$ is the ratio of reactants’ initial concentration and  $R_{A}$,
$R_{A}$,  $R_{B}$ and
$R_{B}$ and  $R_{C}$ are the log-viscosity ratios. We perform numerical simulations of the coupled nonlinear partial differential equations for large values of
$R_{C}$ are the log-viscosity ratios. We perform numerical simulations of the coupled nonlinear partial differential equations for large values of  $Da$. The critical values
$Da$. The critical values  $R_{Phys, c}$ and
$R_{Phys, c}$ and  $R_{Chem, c}$ for instability decrease with
$R_{Chem, c}$ for instability decrease with  $Pe$ and they exhibit power laws in
$Pe$ and they exhibit power laws in  $Pe$. In the asymptotic limit of infinitely large
$Pe$. In the asymptotic limit of infinitely large  $Pe$ they exhibit a power-law dependence on
$Pe$ they exhibit a power-law dependence on  $Pe$ (
$Pe$ ( $R_{Chem, c} \sim Pe^{-1/2}$ as
$R_{Chem, c} \sim Pe^{-1/2}$ as  $Pe \rightarrow \infty$) in both the linear and nonlinear regimes.
$Pe \rightarrow \infty$) in both the linear and nonlinear regimes.