Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pähtz, Thomas
Durán, Orencio
de Klerk, David N.
Govender, Indresan
and
Trulsson, Martin
2019.
Local Rheology Relation with Variable Yield Stress Ratio across Dry, Wet, Dense, and Dilute Granular Flows.
Physical Review Letters,
Vol. 123,
Issue. 4,
Saha, Saikat
and
Alam, Meheboob
2020.
Burnett-order constitutive relations, second moment anisotropy and co-existing states in sheared dense gas–solid suspensions.
Journal of Fluid Mechanics,
Vol. 887,
Issue. ,
Reddy, M. H. Lakshminarayana
and
Alam, Meheboob
2020.
Regularized extended-hydrodynamic equations for a rarefied granular gas and the plane shock waves.
Physical Review Fluids,
Vol. 5,
Issue. 4,
Gómez González, Rubén
and
Garzó, Vicente
2022.
Kinetic theory of granular particles immersed in a molecular gas.
Journal of Fluid Mechanics,
Vol. 943,
Issue. ,
Gómez González, Rubén
and
Garzó, Vicente
2023.
Tracer diffusion coefficients in a moderately dense granular suspension: Stability analysis and thermal diffusion segregation.
Physics of Fluids,
Vol. 35,
Issue. 8,
Faroughi, Salah A.
and
Huber, Christian
2023.
Rheological state variables: A framework for viscosity parametrization in crystal-rich magmas.
Journal of Volcanology and Geothermal Research,
Vol. 440,
Issue. ,
p.
107856.
Gómez González, Rubén
Abad, Enrique
Bravo Yuste, Santos
and
Garzó, Vicente
2023.
Diffusion of intruders in granular suspensions: Enskog theory and random walk interpretation.
Physical Review E,
Vol. 108,
Issue. 2,
Gómez González, Rubén
and
Garzó, Vicente
2024.
Exact Results for Non-Newtonian Transport Properties in Sheared Granular Suspensions: Inelastic Maxwell Models and BGK-Type Kinetic Model.
Entropy,
Vol. 26,
Issue. 3,
p.
265.
Gómez González, Rubén
and
Garzó, Vicente
2024.
Mobility and diffusion of intruders in granular suspensions: Einstein relation.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2024,
Issue. 2,
p.
023211.
González, Rubén Gómez
Yuste, Santos Bravo
and
Garzó, Vicente
2024.
Mean square displacement of intruders in freely cooling multicomponent granular mixtures.
Physical Review E,
Vol. 110,
Issue. 6,
Gómez González, Rubén
García Chamorro, Moisés
and
Garzó, Vicente
2024.
Rheology of granular particles immersed in a molecular gas under uniform shear flow.
Physical Review E,
Vol. 109,
Issue. 6,
Takada, Satoshi
Hara, Kazuhiro
and
Hayakawa, Hisao
2025.
Kinetic Theory of Discontinuous Shear Thickening of a Moderately Dense Inertial Suspension of Frictionless Soft Particles.
Progress of Theoretical and Experimental Physics,
Vol. 2025,
Issue. 2,
Yu, Youhe
Luo, Hongqi
Gu, Yongxia
Zhao, Jieliang
and
Tomaszewska, Ewa
2025.
Distinct roles of claws and adhesive pads in honey bees determine their adhesive performance under varying surface roughness conditions through a dual-mode synergistic adhesion mechanism.
PLOS One,
Vol. 20,
Issue. 8,
p.
e0329624.
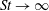 $St\rightarrow \infty$) and its small-Stokes-number counterpart, with quantitative agreement for all transport coefficients. It is shown that the predictions of the shear viscosity and normal-stress differences based on existing theories deteriorate markedly with increasing density as well as with decreasing Stokes number and restitution coefficient.
$St\rightarrow \infty$) and its small-Stokes-number counterpart, with quantitative agreement for all transport coefficients. It is shown that the predictions of the shear viscosity and normal-stress differences based on existing theories deteriorate markedly with increasing density as well as with decreasing Stokes number and restitution coefficient.
