Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dey, Prasanta K.
and
Zikanov, Oleg
2012.
Scalar transport and perturbation dynamics in intermittent magnetohydrodynamic flow.
Physics of Fluids,
Vol. 24,
Issue. 8,
Sethia, Gautam C.
Sen, Abhijit
and
Johnston, George L.
2013.
Amplitude-mediated chimera states.
Physical Review E,
Vol. 88,
Issue. 4,
Wallin, Stefan
Grundestam, Olof
and
Johansson, Arne V.
2013.
Laminarization mechanisms and extreme-amplitude states in rapidly rotating plane channel flow.
Journal of Fluid Mechanics,
Vol. 730,
Issue. ,
p.
193.
Duguet, Yohann
and
Schlatter, Philipp
2013.
Oblique Laminar-Turbulent Interfaces in Plane Shear Flows.
Physical Review Letters,
Vol. 110,
Issue. 3,
Krasnov, Dmitry
Thess, André
Boeck, Thomas
Zhao, Yurong
and
Zikanov, Oleg
2013.
Patterned Turbulence in Liquid Metal Flow: Computational Reconstruction of the Hartmann Experiment.
Physical Review Letters,
Vol. 110,
Issue. 8,
Zikanov, Oleg
Krasnov, Dmitry
Boeck, Thomas
Thess, Andre
and
Rossi, Maurice
2014.
Laminar-Turbulent Transition in Magnetohydrodynamic Duct, Pipe, and Channel Flows.
Applied Mechanics Reviews,
Vol. 66,
Issue. 3,
Brethouwer, Geert
Schlatter, Philipp
Duguet, Yohann
Henningson, Dan S.
and
Johansson, Arne V.
2014.
Recurrent Bursts via Linear Processes in Turbulent Environments.
Physical Review Letters,
Vol. 112,
Issue. 14,
Deusebio, Enrico
Brethouwer, G.
Schlatter, P.
and
Lindborg, E.
2014.
A numerical study of the unstratified and stratified Ekman layer.
Journal of Fluid Mechanics,
Vol. 755,
Issue. ,
p.
672.
Ishida, Takahiro
Tsukahara, Takahiro
and
Kawaguchi, Yasuo
2014.
Large-scale structure alternation in rotating plane Poiseuille flow at transitional Reynolds number.
Applied Thermal Engineering,
Vol. 72,
Issue. 1,
p.
70.
Ansorge, Cedrick
and
Mellado, Juan Pedro
2014.
Global Intermittency and Collapsing Turbulence in the Stratified Planetary Boundary Layer.
Boundary-Layer Meteorology,
Vol. 153,
Issue. 1,
p.
89.
Zikanov, Oleg
Krasnov, Dmitry
Li, Yongqi
Boeck, Thomas
and
Thess, André
2014.
Patterned turbulence in spatially evolving magnetohydrodynamic duct and pipe flows.
Theoretical and Computational Fluid Dynamics,
Vol. 28,
Issue. 3,
p.
319.
Tuckerman, Laurette S.
Kreilos, Tobias
Schrobsdorff, Hecke
Schneider, Tobias M.
and
Gibson, John F.
2014.
Turbulent-laminar patterns in plane Poiseuille flow.
Physics of Fluids,
Vol. 26,
Issue. 11,
Manneville, Paul
2015.
On the transition to turbulence of wall-bounded flows in general, and plane Couette flow in particular.
European Journal of Mechanics - B/Fluids,
Vol. 49,
Issue. ,
p.
345.
Maistrenko, Yuri
Sudakov, Oleksandr
Osiv, Oleksiy
and
Maistrenko, Volodymyr
2015.
Chimera states in three dimensions.
New Journal of Physics,
Vol. 17,
Issue. 7,
p.
073037.
He, P.
and
Basu, S.
2015.
Direct numerical simulation of intermittent turbulence under stably stratified conditions.
Nonlinear Processes in Geophysics,
Vol. 22,
Issue. 4,
p.
447.
Ishida, Takahiro
Tsukahara, Takahiro
and
Kawaguchi, Yasuo
2015.
Effects of spanwise system rotation on turbulent stripes in a plane Poiseuille flow.
Journal of Turbulence,
Vol. 16,
Issue. 3,
p.
273.
Deusebio, Enrico
Caulfield, C. P.
and
Taylor, J. R.
2015.
The intermittency boundary in stratified plane Couette flow.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
298.
Salewski, Matthew
and
Eckhardt, Bruno
2015.
Turbulent states in plane Couette flow with rotation.
Physics of Fluids,
Vol. 27,
Issue. 4,
Gopal, R.
Chandrasekar, V. K.
Senthilkumar, D. V.
Venkatesan, A.
and
Lakshmanan, M.
2015.
Effect of asymmetry parameter on the dynamical states of nonlocally coupled nonlinear oscillators.
Physical Review E,
Vol. 91,
Issue. 6,
He, Ping
and
Basu, Sukanta
2016.
Development of similarity relationships for energy dissipation rate and temperature structure parameter in stably stratified flows: a direct numerical simulation approach.
Environmental Fluid Mechanics,
Vol. 16,
Issue. 2,
p.
373.
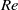 by increasing the damping by the Coriolis, buoyancy or Lorentz force. We show evidence for this phenomenon in three distinct flow cases: plane Couette flow with spanwise cyclonic rotation, plane magnetohydrodynamic channel flow with a spanwise or wall-normal magnetic field, and open channel flow under stable stratification. Near-wall turbulence structures inside the turbulent patterns are invariably found to scale in terms of viscous wall units as in the fully turbulent case, while the patterns themselves remain large-scale with a trend towards shorter wavelength for increasing
by increasing the damping by the Coriolis, buoyancy or Lorentz force. We show evidence for this phenomenon in three distinct flow cases: plane Couette flow with spanwise cyclonic rotation, plane magnetohydrodynamic channel flow with a spanwise or wall-normal magnetic field, and open channel flow under stable stratification. Near-wall turbulence structures inside the turbulent patterns are invariably found to scale in terms of viscous wall units as in the fully turbulent case, while the patterns themselves remain large-scale with a trend towards shorter wavelength for increasing 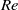 . Two distinct regimes are identified: at low Reynolds numbers the patterns extend from one wall to the other, while at large Reynolds number they are confined to the near-wall regions and the patterns on both channel sides are uncorrelated, the core of the flow being highly turbulent without any dominant large-scale structure.
. Two distinct regimes are identified: at low Reynolds numbers the patterns extend from one wall to the other, while at large Reynolds number they are confined to the near-wall regions and the patterns on both channel sides are uncorrelated, the core of the flow being highly turbulent without any dominant large-scale structure.
