Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-24T14:11:52.870Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent wake behind a concave curved cylinder

Published online by Cambridge University Press:  18 September 2019

Fengjian Jiang Open the ORCID record for Fengjian Jiang [Opens in a new window] ,
Bjørnar Pettersen  and
Helge I. Andersson
Fengjian Jiang*
Affiliation:
Department of Marine Technology, Norwegian University of Science and Technology (NTNU), 7491 Trondheim, NO-7491, Norway
Bjørnar Pettersen
Affiliation:
Department of Marine Technology, Norwegian University of Science and Technology (NTNU), 7491 Trondheim, NO-7491, Norway
Helge I. Andersson
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology (NTNU), 7491 Trondheim, NO-7491, Norway
*
†Email address for correspondence: fengjian.jiang@outlook.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a detailed study of the turbulent wake behind a quarter-ring curved cylinder at Reynolds number 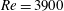$Re=3900$ (based on cylinder diameter and incoming flow velocity), by means of direct numerical simulation. The configuration is referred to as a concave curved cylinder with incoming flow aligned with the plane of curvature and towards the inner face of the cylinder. Wake flows behind this configuration are known to be complex, but have so far only been studied at low 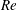$Re$. This is the first direct numerical simulation investigation of the turbulent wake behind the concave configuration, from which we reveal new and interesting wake dynamics, and present in-depth physical interpretations. Similar to the low-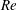$Re$ cases, the turbulent wake behind a concave curved cylinder is a multi-regime and multi-frequency flow. However, in addition to the coexisting flow regimes reported at lower 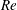$Re$, we observe a new transitional flow regime at 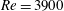$Re=3900$. The flow field in this transitional regime is dominated not by von Kármán-type vortex shedding, but by periodic asymmetric helical vortices. Such vortex pairs exist also in some other wake flows, but are then non-periodic. Inspections reveal that the periodic motion of the asymmetric helical vortices is induced by vortex shedding in its neighbouring oblique shedding regime. The oblique shedding regime is in turn influenced by the transitional regime, resulting in a unified and remarkably low dominating frequency in both flow regimes. Owing to this synchronized frequency, the new wake dynamics in the transitional regime might easily be overlooked. In the near wake, two distinct peaks are observed in the time-averaged axial velocity distribution along the curved cylinder span, while only one peak was observed at lower 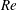$Re$. The presence of the additional peak is ascribed to a strong favourable base pressure gradient along the cylinder span. It is noteworthy that the axially directed base flow exceeded the incoming velocity behind a substantial part of the quarter-ring and even persisted upwards along the straight vertical extension. As a by-product of our study, we find that a straight vertical extension of 16 cylinder diameters is required in order to avoid any adverse effects from the upper boundary of the flow domain.

JFM classification

Wakes/Jets: Wakes Vortex Flows: Vortex shedding Wakes/Jets: Separated flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , pp. 663 - 699
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andersson, H. I., Jiang, F. & Okulov, V. L. 2019 Instabilities in the wake of an inclined prolate spheroid. In Computational Modelling of Bifurcations and Instabilities in Fluid Dynamics (ed. Gelfgat, A.), Computational Methods in Applied Sciences, vol. 50, pp. 311–352. Springer.Google Scholar
Assi, G. R. S., Srinil, N., Freire, C. M. & Korkischko, I. 2014 Experimental investigation of the flow-induced vibration of a curved cylinder in convex and concave configurations. J. Fluids Struct. 44, 52–66.Google Scholar
Beaudan, P. & Moin, P.1994 Numerical experiments on the flow past a circular cylinder at sub-critical Reynolds number. Tech. Rep. TF-62. Department of Mechanical Engineering, Stanford University.Google Scholar
Dong, S., Karniadakis, G. E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation-particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207.Google Scholar
Gallardo, J. P., Pettersen, B. & Andersson, H. I. 2013 Effects of free-slip boundary conditions on the flow around a curved circular cylinder. Comput. Fluids 86, 389–394.Google Scholar
Gallardo, J. P., Pettersen, B. & Andersson, H. I. 2014a Turbulent wake behind a curved circular cylinder. J. Fluid Mech. 742, 192–229.Google Scholar
Gallardo, J. P., Pettersen, B. & Andersson, H. I. 2014b Coherence and Reynolds stresses in the turbulent wake behind a curved circular cylinder. J. Turbul. 15, 883–904.Google Scholar
Gerrard, J. H. 1978 The wakes of cylindrical bluff bodies at low Reynolds number. Phil. Trans. R. Soc. Lond. A 288, 351–382.Google Scholar
Jacob, J., Malaspinas, O. & Sagaut, P. 2018 A new hybrid recursive regularised Bhatnagar–Gross–Krook collision model for Lattice Boltzmann method-based large eddy simulation. J. Turbul. 19, 1–26.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jiang, F., Gallardo, J. P., Andersson, H. I. & Okulov, V. L. 2016 On the peculiar structure of a helical wake vortex behind an inclined prolate spheroid. J. Fluid Mech. 801, 1–12.Google Scholar
Jiang, F., Gallardo, J. P., Andersson, H. I. & Zhang, Z. 2015 The transitional wake behind an inclined prolate spheroid. Phys. Fluids 27, 093602.Google Scholar
Jiang, F., Pettersen, B. & Andersson, H. I. 2018a Influences of upstream extensions on flow around a curved cylinder. Eur. J. Mech. (B/Fluids) 67, 79–86.Google Scholar
Jiang, F., Pettersen, B., Andersson, H. I., Kim, J. & Kim, S. 2018b Wake behind a concave curved cylinder. Phys. Rev. Fluids 3, 094804.Google Scholar
Jung, J.-H., Oh, S., Nam, B.-W., Park, B., Kwon, Y.-J. & Jung, D. 2019 Numerical study on flow characteristics around curved riser. J. Ocean Engng Technol. 33, 123–130.Google Scholar
Kravchenko, A. G. & Moin, P. 2000 Numerical studies of flow over a circular cylinder at Re = 3900. Phys. Fluids 12, 403–417.Google Scholar
Leontini, J. S., Jacono, D. L. & Thompson, M. C. 2015 Stability analysis of the elliptic cylinder wake. J. Fluid Mech. 763, 302–321.Google Scholar
Lin, J.-C., Towfighi, J. & Rockwell, D. 1995 Instantaneous structure of the near-wake of a circular cylinder: on the effect of Reynolds number. J. Fluids Struct. 9, 409–418.Google Scholar
Ma, B. & Yin, S. 2018 Vortex oscillations around a hemisphere-cylinder body with a high fineness ratio. AIAA J. 56, 1402–1420.Google Scholar
Ma, X., Karamanos, G.-S. & Karniadakis, G. E. 2000 Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 410, 29–65.Google Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197, 215–240.Google Scholar
Manhart, M. 2004 A zonal grid algorithm for DNS of turbulent boundary layers. Comput. Fluids 33, 435–461.Google Scholar
Manhart, M., Tremblay, F. & Friedrich, R. 2001 MGLET: a parallel code for efficient DNS and LES of complex geometries. In Parallel Computational Fluid Dynamics – Trends and Applications (ed. Jenssen, C. B., Kvamsdal, T., Andersson, H. I., Pettersen, B., Ecer, A., Periaux, J., Satofuka, N. & Fox, P.), pp. 449–456. Elsevier.Google Scholar
Miliou, A., de Vecchi, A., Sherwin, S. J. & Graham, J. M. R. 2007 Wake dynamics of external flow past a curved circular cylinder with the free stream aligned with the plane of curvature. J. Fluid Mech. 592, 89–115.Google Scholar
Ong, J. & Wallace, L. 1999 The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 20, 441–453.Google Scholar
Parnaudeau, P., Carlier, J., Heitz, D. & Lamballais, E. 2008 Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 20, 085101.Google Scholar
Paul, I., Prakash, K. A., Vengadesan, S. & Pulletikurthi, V. 2016 Analysis and characterisation of momentum and thermal wakes of elliptic cylinders. J. Fluid Mech. 807, 303–323.Google Scholar
Peller, N., Le Duc, A., Tremblay, F. & Manhart, M. 2006 High-order stable interpolations for immersed boundary methods. Intl J. Numer. Meth. Fluids 52, 1175–1193.Google Scholar
Prasad, A. & Williamson, C. H. K. 1997 The instability of the shear layer separating from a bluff body. J. Fluid Mech. 333, 375–402.Google Scholar
Ramberg, S. 1983 The effects of yaw and finite length upon the vortex wakes of stationary and vibrating circular cylinders. J. Fluid Mech. 128, 81–107.Google Scholar
Roshko, A. 1993 Perspectives on bluff body aerodynamics. J. Wind Engng Ind. Aerodyn. 49, 79–100.Google Scholar
Serson, D., Meneghini, J. R., Carmo, B. S., Volpe, E. V. & Gioria, R. S. 2014 Wake transition in the flow around a circular cylinder with a splitter plate. J. Fluid Mech. 755, 582–602.Google Scholar
Shang, J. K., Stone, H. A. & Smits, A. J. 2018 Flow past finite cylinders of constant curvature. J. Fluid Mech. 837, 896–915.Google Scholar
Shirakashi, M., Hasegawa, A. & Wakiya, S. 1986 Effect of the secondary flow on Kármán vortex shedding from a yawed cylinder. Bull. JSME 29, 1124–1128.Google Scholar
Snarski, S. R. 2004 Flow over yawed circular cylinders: wall pressure spectra and flow regimes. Phys. Fluids 16, 344–359.Google Scholar
Srinil, N. 2010 Multi-mode interactions in vortex-induced vibrations of flexible curved/straight structures with geometric nonlinearities. J. Fluids Struct. 26, 1098–1122.Google Scholar
Srinil, N., Ma, B. & Zhang, L. 2018 Experimental investigation on in-plane/out-of-plane vortex-induced vibrations of curved cylinder in parallel and perpendicular flows. J. Sound Vib. 421, 275–299.Google Scholar
Stone, H. L. 1968 Iterative solution of implicit approximations of multidimensional partial differential equations. SIAM J. Numer. Anal. 5, 530–558.Google Scholar
Strandenes, H., Jiang, F., Pettersen, B. & Andersson, H. I. 2019 Near-wake of an inclined 6 : 1 spheroid at Reynolds number 4000. AIAA J. 57, 1364–1372.Google Scholar
Strandenes, H., Pettersen, B., Andersson, H. I. & Manhart, M. 2017 Influence of spanwise no-slip boundary conditions on the flow around a cylinder. Comput. Fluids 156, 48–57.Google Scholar
Sumer, B. M. & Fredsøe, J. 2006 Hydrodynamics Around Cylindrical Structures, revised edn. World Scientific.Google Scholar
Thomson, K. D. & Morrison, D. F. 1971 The spacing, position and strength of vortices in the wake of slender cylindrical bodies at large incidence. J. Fluid Mech. 50, 751–783.Google Scholar
Tian, C., Jiang, F., Pettersen, B. & Andersson, H. I. 2017 Antisymmetric vortex interactions in the wake behind a step cylinder. Phys. Fluids 29, 101704.Google Scholar
de Vecchi, A., Sherwin, S. J. & Graham, J. M. R. 2008 Wake dynamics of external flow past a curved circular cylinder with the free-stream aligned to the plane of curvature. J. Fluids Struct. 24, 1262–1270.Google Scholar
de Vecchi, A., Sherwin, S. J. & Graham, J. M. R. 2009 Wake dynamics past a curved body of circular cross-section under forced cross-flow vibration. J. Fluids Struct. 25, 721–730.Google Scholar
Welch, P. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15, 70–73.Google Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Williamson, J. H. 1980 Low-storage Runge–Kutta schemes. J. Comput. Phys. 56, 53–63.Google Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders. Oxford University Press.Google Scholar
Zhao, M., Cheng, L. & Zhou, T. 2009 Direct numerical simulation of three-dimensional flow past a yawed circular cylinder of infinite length. J. Fluids Struct. 25, 831–847.Google Scholar
Zhu, H., Bao, Y., Zhou, D. & Wang, R. 2017 Direct numerical simulation of the flow past a stationary catenary riser at low Reynolds number. In Proceedings of the Twenty-Seventh International Ocean and Polar Engineering Conference, pp. 127–134. International Society of Offshore and Polar Engineers.Google Scholar
Zhu, H., Wang, R., Bao, Y., Zhou, D., Ping, H., Han, Z. & Sherwin, S. J. 2019 Flow over a symmetrically curved circular cylinder with the free stream parallel to the plane of curvature at low Reynolds number. J. Fluids Struct. 87, 23–38.Google Scholar
Zhu, H., Zhou, D., Bao, Y., Wang, R., Lu, J., Fan, D. & Han, Z. 2018 Wake characteristics of stationary catenary risers with differnt incoming flow directions. Ocean Engng 167, 142–155.Google Scholar

Jiang et al. supplementary movie 1

A movie of instantaneous cross-flow velocity distribution in the symmetry plane.

Download Jiang et al. supplementary movie 1(Video)
Video 8.7 MB

Jiang et al. supplementary movie 2

Wake dynamics in the z/D = -7.0 plane.

Download Jiang et al. supplementary movie 2(Video)
Video 4 MB

Jiang et al. supplementary movie 3

Wake dynamics in the z/D = -6.0 plane.

Download Jiang et al. supplementary movie 3(Video)
Video 5.8 MB

Jiang et al. supplementary movie 4

Wake dynamics in the x/D = 14.0 plane.

Download Jiang et al. supplementary movie 4(Video)
Video 8.1 MB