Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kourmatzis, Agissilaos
Ergene, Egemen L.
Shrimpton, John S.
Kyritsis, Dimitrios C.
Mashayek, Farzad
and
Huo, Ming
2012.
Combined aerodynamic and electrostatic atomization of dielectric liquid jets.
Experiments in Fluids,
Vol. 53,
Issue. 1,
p.
221.
Wu, Jian
Traore, Philippe
Louste, Christophe
Dascalescu, Lucian
Fang-Bao Tian
and
Perez, Alberto
2013.
Numerical investigation of electrohydrodynamic plumes for locally enhanced cooling in dielectric liquids.
p.
1.
Traoré, Philippe
and
Wu, Jian
2013.
On the limitation of imposed velocity field strategy for Coulomb-driven electroconvection flow simulations.
Journal of Fluid Mechanics,
Vol. 727,
Issue. ,
Wu, Jian
Traore, Philippe
Louste, Christophe
Dascalescu, Lucian
Fang-Bao Tian
and
Perez, Alberto
2013.
Effect of the mobility parameter on the oscillatory electro-convection of dielectric liquids subject to strong unipolar charge injection.
p.
1.
Wu, Jian
Traore, Philippe
and
Tian, Fang-Bao
2013.
Three-dimensional numerical simulation of electro-convection due to strong unipolar charge injection in a cubic cavity.
p.
1038.
Wu, Jian
Traore, Philippe
Louste, Christophe
Dascalescu, Lucian
Tian, Fang-Bao
and
Perez, Alberto T.
2014.
Effect of the Mobility Parameter on the Oscillatory Electroconvection of Dielectric Liquids Subject to Strong Unipolar Charge Injection.
IEEE Transactions on Industry Applications,
Vol. 50,
Issue. 4,
p.
2306.
Wu, Jian
Vázquez, Pédro A.
Traoré, Philippe
and
Pérez, Alberto T.
2014.
Finite amplitude electroconvection induced by strong unipolar injection between two coaxial cylinders.
Physics of Fluids,
Vol. 26,
Issue. 12,
Zhang, X.
2014.
Electro-optic signatures of turbulent electroconvection in dielectric liquids.
Applied Physics Letters,
Vol. 104,
Issue. 20,
Kourmatzis, A.
and
Shrimpton, J. S.
2014.
Electrohydrodynamic inter-electrode flow and liquid jet characteristics in charge injection atomizers.
Experiments in Fluids,
Vol. 55,
Issue. 3,
Wu, Jian
Traoré, Philippe
Pérez, Alberto T.
and
Zhang, Mengqi
2015.
Numerical analysis of the subcritical feature of electro-thermo-convection in a plane layer of dielectric liquid.
Physica D: Nonlinear Phenomena,
Vol. 311-312,
Issue. ,
p.
45.
Zhang, Mengqi
Martinelli, Fulvio
Wu, Jian
Schmid, Peter J.
and
Quadrio, Maurizio
2015.
Modal and non-modal stability analysis of electrohydrodynamic flow with and without cross-flow.
Journal of Fluid Mechanics,
Vol. 770,
Issue. ,
p.
319.
Wu, Jian
Traoré, Philippe
Pérez, Alberto T.
and
Vázquez, Pédro A.
2015.
On two-dimensional finite amplitude electro-convection in a dielectric liquid induced by a strong unipolar injection.
Journal of Electrostatics,
Vol. 74,
Issue. ,
p.
85.
Wu, Jian
and
Traoré, Philippe
2015.
A Finite-Volume Method for Electro-Thermoconvective Phenomena in a Plane Layer of Dielectric Liquid.
Numerical Heat Transfer, Part A: Applications,
Vol. 68,
Issue. 5,
p.
471.
Wu, Jian
Traore, Philippe
Louste, Christophe
Dascalescu, Lucian
Tian, Fang-Bao
and
Perez, Alberto T.
2015.
Numerical Investigation of Electrohydrodynamic Plumes for Locally Enhanced Cooling in Dielectric Liquids.
IEEE Transactions on Industry Applications,
Vol. 51,
Issue. 1,
p.
669.
Kourmatzis, Agisilaos
and
Shrimpton, John S
2016.
Characteristics of electrohydrodynamic roll structures in laminar planar Couette flow.
Journal of Physics D: Applied Physics,
Vol. 49,
Issue. 4,
p.
045503.
Zhao, Wei
and
Wang, Guiren
2017.
Scaling of velocity and scalar structure functions in ac electrokinetic turbulence.
Physical Review E,
Vol. 95,
Issue. 2,
Luo, Kang
Wu, Jian
Yi, Hong-Liang
and
Tan, He-Ping
2018.
Three-dimensional finite amplitude electroconvection in dielectric liquids.
Physics of Fluids,
Vol. 30,
Issue. 2,
Luo, Kang
Li, Tian-Fu
Wu, Jian
Yi, Hong-Liang
and
Tan, He-Ping
2018.
Mesoscopic simulation of electrohydrodynamic effects on laminar natural convection of a dielectric liquid in a cubic cavity.
Physics of Fluids,
Vol. 30,
Issue. 10,
Luo, Kang
Wu, Jian
Yi, Hong-Liang
Liu, Lin-Hua
and
Tan, He-Ping
2018.
Hexagonal convection patterns and their evolutionary scenarios in electroconvection induced by a strong unipolar injection.
Physical Review Fluids,
Vol. 3,
Issue. 5,
Kourmatzis, A.
and
Shrimpton, J.S.
2018.
Turbulence closure models for free electroconvection.
International Journal of Heat and Fluid Flow,
Vol. 71,
Issue. ,
p.
153.
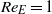 ) and high electric Reynolds numbers (up to
) and high electric Reynolds numbers (up to 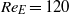 ). Furthermore, calculations of mean profiles and second-order moments along with energy budgets and spectra have examined the validity of neglecting the fluctuating electric field
). Furthermore, calculations of mean profiles and second-order moments along with energy budgets and spectra have examined the validity of neglecting the fluctuating electric field 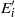 in the Reynolds-averaged EHD equations and provide insight into the generation and transport mechanisms of turbulent EHD. Spectral and spatial data clearly indicate how fluctuating energy is transferred from electrical to hydrodynamic forms, on moving through the domain away from the charging electrode. It is shown that
in the Reynolds-averaged EHD equations and provide insight into the generation and transport mechanisms of turbulent EHD. Spectral and spatial data clearly indicate how fluctuating energy is transferred from electrical to hydrodynamic forms, on moving through the domain away from the charging electrode. It is shown that  is not negligible close to the walls and terms acting as sources and sinks in the turbulent kinetic energy, turbulent scalar flux and turbulent scalar variance equations are examined. Profiles of hydrodynamic terms in the budgets resemble those in the literature for RBC; however there are terms specific to EHD that are significant, indicating that the transfer of energy in EHD is also attributed to further electrodynamic terms and a strong coupling exists between the charge flux and variance, due to the ionic drift term.
is not negligible close to the walls and terms acting as sources and sinks in the turbulent kinetic energy, turbulent scalar flux and turbulent scalar variance equations are examined. Profiles of hydrodynamic terms in the budgets resemble those in the literature for RBC; however there are terms specific to EHD that are significant, indicating that the transfer of energy in EHD is also attributed to further electrodynamic terms and a strong coupling exists between the charge flux and variance, due to the ionic drift term.