Article contents
Turbulent flow in the bulk of Rayleigh–Bénard convection: small-scale properties in a cubic cell
Published online by Cambridge University Press: 28 March 2013
Abstract
The Rayleigh number ( 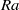 $\mathit{Ra}$ ) scaling of the global Bolgiano length scale
$\mathit{Ra}$ ) scaling of the global Bolgiano length scale  ${L}_{B, global} $ and the local Bolgiano length scale
${L}_{B, global} $ and the local Bolgiano length scale 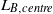 ${L}_{B, centre} $ in the centre region of turbulent Rayleigh–Bénard convection are investigated for Prandtl numbers
${L}_{B, centre} $ in the centre region of turbulent Rayleigh–Bénard convection are investigated for Prandtl numbers 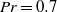 $\mathit{Pr}= 0. 7$ and
$\mathit{Pr}= 0. 7$ and 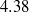 $4. 38$ and
$4. 38$ and 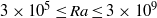 $3\times 1{0}^{5} \leq \mathit{Ra}\leq 3\times 1{0}^{9} $ . It is found that
$3\times 1{0}^{5} \leq \mathit{Ra}\leq 3\times 1{0}^{9} $ . It is found that 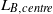 ${L}_{B, centre} $ does not necessarily exhibit the same scaling as
${L}_{B, centre} $ does not necessarily exhibit the same scaling as 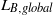 ${L}_{B, global} $ . While
${L}_{B, global} $ . While 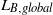 ${L}_{B, global} $ is monotonically deceasing as
${L}_{B, global} $ is monotonically deceasing as 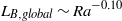 ${L}_{B, global} \sim {\mathit{Ra}}^{- 0. 10} $ for both
${L}_{B, global} \sim {\mathit{Ra}}^{- 0. 10} $ for both 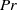 $\mathit{Pr}$ ,
$\mathit{Pr}$ , 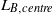 ${L}_{B, centre} $ shows a steep increase beyond a certain
${L}_{B, centre} $ shows a steep increase beyond a certain 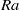 $\mathit{Ra}$ value. The complex scaling of the local Bolgiano length scale in the centre is a result of the different behaviour of the temperature-variance dissipation rate,
$\mathit{Ra}$ value. The complex scaling of the local Bolgiano length scale in the centre is a result of the different behaviour of the temperature-variance dissipation rate, 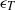 ${\epsilon }_{T} $ , and the turbulent-kinetic-energy dissipation rate,
${\epsilon }_{T} $ , and the turbulent-kinetic-energy dissipation rate, 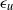 ${\epsilon }_{u} $ . This shows that for sufficiently high
${\epsilon }_{u} $ . This shows that for sufficiently high 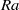 $\mathit{Ra}$ the flow is well-mixed and hence temperature is passively advected. It is also observed that the
$\mathit{Ra}$ the flow is well-mixed and hence temperature is passively advected. It is also observed that the 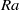 $\mathit{Ra}$ -range in which
$\mathit{Ra}$ -range in which 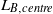 ${L}_{B, centre} $ exhibits the same scaling as the global Bolgiano length scale is increasing with increasing
${L}_{B, centre} $ exhibits the same scaling as the global Bolgiano length scale is increasing with increasing 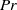 $\mathit{Pr}$ . It is further observed that for
$\mathit{Pr}$ . It is further observed that for 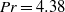 $\mathit{Pr}= 4. 38$ and
$\mathit{Pr}= 4. 38$ and 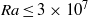 $\mathit{Ra}\leq 3\times 1{0}^{7} $ the local vertical heat flux in the centre region is balanced by the turbulent-kinetic-energy dissipation rate. For higher
$\mathit{Ra}\leq 3\times 1{0}^{7} $ the local vertical heat flux in the centre region is balanced by the turbulent-kinetic-energy dissipation rate. For higher 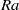 $\mathit{Ra}$ we find that the local heat flux is decreasing. At
$\mathit{Ra}$ we find that the local heat flux is decreasing. At 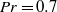 $\mathit{Pr}= 0. 7$ we do not observe such a balance, as the measured heat flux is between the heat fluxes estimated through the turbulent-kinetic-energy dissipation rate and the temperature-variance dissipation rate. We therefore suggest that the balance of the local heat flux might be Prandtl-number dependent. The conditional average of the local vertical heat flux
$\mathit{Pr}= 0. 7$ we do not observe such a balance, as the measured heat flux is between the heat fluxes estimated through the turbulent-kinetic-energy dissipation rate and the temperature-variance dissipation rate. We therefore suggest that the balance of the local heat flux might be Prandtl-number dependent. The conditional average of the local vertical heat flux 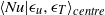 $\mathop{\langle \mathit{Nu}\vert {\epsilon }_{u} , {\epsilon }_{T} \rangle }\nolimits_{\mathit{centre}} $ in the core region of the flow reveals that the highest vertical heat flux occurs for rare events with very high dissipation rates, while the joint most probable dissipation rates are associated with very low values of vertical heat flux. It is also observed that high values of
$\mathop{\langle \mathit{Nu}\vert {\epsilon }_{u} , {\epsilon }_{T} \rangle }\nolimits_{\mathit{centre}} $ in the core region of the flow reveals that the highest vertical heat flux occurs for rare events with very high dissipation rates, while the joint most probable dissipation rates are associated with very low values of vertical heat flux. It is also observed that high values of 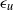 ${\epsilon }_{u} $ and
${\epsilon }_{u} $ and 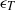 ${\epsilon }_{T} $ tend to occur together. It is further observed that the longitudinal velocity structure functions approach Kolmogorov K41 scaling. The temperature structure functions appear to approach Bolgiano–Obukhov BO59 scaling for
${\epsilon }_{T} $ tend to occur together. It is further observed that the longitudinal velocity structure functions approach Kolmogorov K41 scaling. The temperature structure functions appear to approach Bolgiano–Obukhov BO59 scaling for 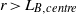 $r\gt {L}_{B, centre} $ , while a scaling exponent smaller than the BO59 scaling is observed for separations
$r\gt {L}_{B, centre} $ , while a scaling exponent smaller than the BO59 scaling is observed for separations 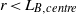 $r\lt {L}_{B, centre} $ . The mixed velocity and temperature structure function for
$r\lt {L}_{B, centre} $ . The mixed velocity and temperature structure function for 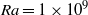 $\mathit{Ra}= 1\times 1{0}^{9} $ and
$\mathit{Ra}= 1\times 1{0}^{9} $ and 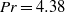 $\mathit{Pr}= 4. 38$ shows a short
$\mathit{Pr}= 4. 38$ shows a short 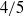 $4/ 5$ -scaling for
$4/ 5$ -scaling for 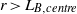 $r\gt {L}_{B, centre} $ . Our results suggest that BO59 scaling might be more clearly observable at higher Prandtl and moderate Rayleigh numbers.
$r\gt {L}_{B, centre} $ . Our results suggest that BO59 scaling might be more clearly observable at higher Prandtl and moderate Rayleigh numbers.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 79
- Cited by

