Article contents
Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects
Published online by Cambridge University Press: 21 August 2012
Abstract
A recent assessment of available direct numerical simulation (DNS) data from turbulent boundary layer flows (Schlatter & Örlü, J. Fluid Mech., vol. 659, 2010, pp. 116–126) showed surprisingly large differences not only in the skin friction coefficient or shape factor, but also in their predictions of mean and fluctuation profiles far into the sublayer. While such differences are expected at very low Reynolds numbers and/or the immediate vicinity of the inflow or tripping region, it remains unclear whether inflow and tripping effects explain the differences observed even at moderate Reynolds numbers. This question is systematically addressed by re-simulating the DNS of a zero-pressure-gradient turbulent boundary layer flow by Schlatter et al. (Phys. Fluids, vol. 21, 2009, art. 051702). The previous DNS serves as the baseline simulation, and the new DNS with a range of physically different inflow conditions and tripping effects are carefully compared. The downstream evolution of integral quantities as well as mean and fluctuation profiles is analysed, and the results show that different inflow conditions and tripping effects do indeed explain most of the differences observed when comparing available DNS at low Reynolds number. It is further found that, if transition is initiated inside the boundary layer at a low enough Reynolds number (based on the momentum-loss thickness) 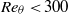 , all quantities agree well for both inner and outer layer for
, all quantities agree well for both inner and outer layer for 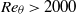 . This result gives a lower limit for meaningful comparisons between numerical and/or wind tunnel experiments, assuming that the flow was not severely over- or understimulated. It is further shown that even profiles of the wall-normal velocity fluctuations and Reynolds shear stress collapse for higher
. This result gives a lower limit for meaningful comparisons between numerical and/or wind tunnel experiments, assuming that the flow was not severely over- or understimulated. It is further shown that even profiles of the wall-normal velocity fluctuations and Reynolds shear stress collapse for higher 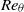 irrespective of the upstream conditions. In addition, the overshoot in the total shear stress within the sublayer observed in the DNS of Wu & Moin (Phys. Fluids, vol. 22, 2010, art. 085105) has been identified as a feature of transitional boundary layers.
irrespective of the upstream conditions. In addition, the overshoot in the total shear stress within the sublayer observed in the DNS of Wu & Moin (Phys. Fluids, vol. 22, 2010, art. 085105) has been identified as a feature of transitional boundary layers.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 242
- Cited by

