Article contents
Turbulent boundary layers absent mean shear
Published online by Cambridge University Press: 27 November 2017
Abstract
We perform an experimental study to investigate the turbulent boundary layer above a stationary solid glass bed in the absence of mean shear. High Reynolds number 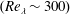 $(Re_{\unicode[STIX]{x1D706}}\sim 300)$ horizontally homogeneous isotropic turbulence is generated via randomly actuated synthetic jet arrays (RASJA – Variano & Cowen J. Fluid Mech. vol. 604, 2008, pp. 1–32). Each of the arrays is controlled by a spatio-temporally varying algorithm, which in turn minimizes the formation of secondary mean flows. One array consists of an
$(Re_{\unicode[STIX]{x1D706}}\sim 300)$ horizontally homogeneous isotropic turbulence is generated via randomly actuated synthetic jet arrays (RASJA – Variano & Cowen J. Fluid Mech. vol. 604, 2008, pp. 1–32). Each of the arrays is controlled by a spatio-temporally varying algorithm, which in turn minimizes the formation of secondary mean flows. One array consists of an 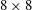 $8\times 8$ grid of jets, while the other is a
$8\times 8$ grid of jets, while the other is a 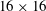 $16\times 16$ array. Particle image velocimetry measurements are used to study the isotropic turbulent region and the boundary layer formed beneath as the turbulence encounters a stationary wall. The flow is characterized with statistical metrics including the mean flow and turbulent velocities, turbulent kinetic energy, integral scales and the turbulent kinetic energy transport equation, which includes the energy dissipation rate, production and turbulent transport. The empirical constant in the Tennekes (J. Fluid Mech. vol. 67, 1975, pp. 561–567) model of Eulerian frequency spectra is calculated based on the dissipation results and temporal frequency spectra from acoustic Doppler velocimetry measurements. We compare our results to prior literature that addresses mean shear free turbulent boundary layer characterizations via grid-stirred tank experiments, moving-bed experiments, rapid-distortion theory and direct numerical simulations in a forced turbulent box. By varying the operational parameters of the randomly actuated synthetic jet array, we also find that we are able to control the turbulence levels, including integral length scales and dissipation rates, by changing the mean on-times in the jet algorithm.
$16\times 16$ array. Particle image velocimetry measurements are used to study the isotropic turbulent region and the boundary layer formed beneath as the turbulence encounters a stationary wall. The flow is characterized with statistical metrics including the mean flow and turbulent velocities, turbulent kinetic energy, integral scales and the turbulent kinetic energy transport equation, which includes the energy dissipation rate, production and turbulent transport. The empirical constant in the Tennekes (J. Fluid Mech. vol. 67, 1975, pp. 561–567) model of Eulerian frequency spectra is calculated based on the dissipation results and temporal frequency spectra from acoustic Doppler velocimetry measurements. We compare our results to prior literature that addresses mean shear free turbulent boundary layer characterizations via grid-stirred tank experiments, moving-bed experiments, rapid-distortion theory and direct numerical simulations in a forced turbulent box. By varying the operational parameters of the randomly actuated synthetic jet array, we also find that we are able to control the turbulence levels, including integral length scales and dissipation rates, by changing the mean on-times in the jet algorithm.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 16
- Cited by


