Article contents
Triadic resonances driven by thermal convection in a rotating sphere
Published online by Cambridge University Press: 23 December 2020
Abstract
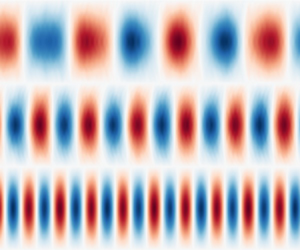
We report for the first time on triadic resonances in a rotating convection system. Using direct numerical simulations, we find that convective modes in a rotating spherical fluid can excite a pair of inertial modes whose frequencies and wavenumbers match the triadic resonance conditions. Depending on the structures of the convective modes, triadic resonances can lead to the growth of either a pair of modes with lower frequencies and wavenumbers, or a pair of modes with higher frequencies and wavenumbers, providing a possible mechanism for the bi-directional energy cascade. Increased thermal forcing leads to fully developed turbulence, which also exhibits wave-like motions, and is reminiscent of the energy spectrum of inertial wave turbulence. Our results suggest that the interaction of inertial waves plays an important role in rotating convection, which is of great importance in understanding the dynamics of planetary and stellar interiors.
Information
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 10
- Cited by


