Article contents
Topological bifurcations of vortex pair interactions
Published online by Cambridge University Press: 23 April 2021
Abstract
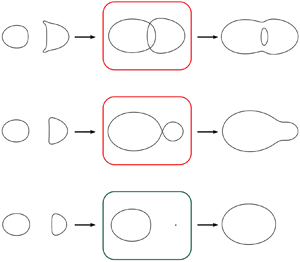
We investigate vortex pair interactions at low Reynolds numbers. We base our analysis on the Q-criterion, where a vortex is defined as a region where the local rotation dominates the strain, and we make use of a topological approach to describe the qualitative changes of the vortex structure. In order to give a complete description of vortex pair interactions we further develop a general bifurcation theory for  $Q$-vortices and prove that a threshold for vortex merging may occur when we allow two parameters to vary. To limit the number of free parameters, we study the interactions with two point vortices as the initial condition and show that the threshold is a codimension two bifurcation that appears as a cusp singularity on a bifurcation curve. We apply the general theory to the analytically tractable core growth model and conclude that a pair of co-rotating vortices merge only if their strength ratio,
$Q$-vortices and prove that a threshold for vortex merging may occur when we allow two parameters to vary. To limit the number of free parameters, we study the interactions with two point vortices as the initial condition and show that the threshold is a codimension two bifurcation that appears as a cusp singularity on a bifurcation curve. We apply the general theory to the analytically tractable core growth model and conclude that a pair of co-rotating vortices merge only if their strength ratio,  $\alpha =\varGamma _1/\varGamma _2$ is less than
$\alpha =\varGamma _1/\varGamma _2$ is less than  $4.58$. Below this threshold value, we observe two different regimes in which the merging processes can be described with different sequences of bifurcations. By comparison with Navier–Stokes simulations at different Reynolds numbers, we conclude that the merging threshold varies only slightly for Reynolds numbers up to
$4.58$. Below this threshold value, we observe two different regimes in which the merging processes can be described with different sequences of bifurcations. By comparison with Navier–Stokes simulations at different Reynolds numbers, we conclude that the merging threshold varies only slightly for Reynolds numbers up to  $100$. Furthermore, we observe an excellent agreement between the core growth model and the numerical simulations for Reynolds numbers below 10. We therefore conclude that, instead of solving the Navier–Stokes equation numerically we can, for sufficiently small Reynolds numbers, apply the core growth model as a simple, analytically tractable model with a low dimension.
$100$. Furthermore, we observe an excellent agreement between the core growth model and the numerical simulations for Reynolds numbers below 10. We therefore conclude that, instead of solving the Navier–Stokes equation numerically we can, for sufficiently small Reynolds numbers, apply the core growth model as a simple, analytically tractable model with a low dimension.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by


